
Question and Answers Forum
Question Number 131887 by Algoritm last updated on 09/Feb/21
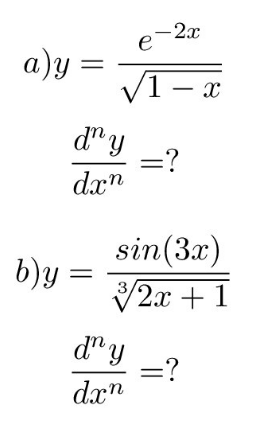
Answered by SEKRET last updated on 09/Feb/21
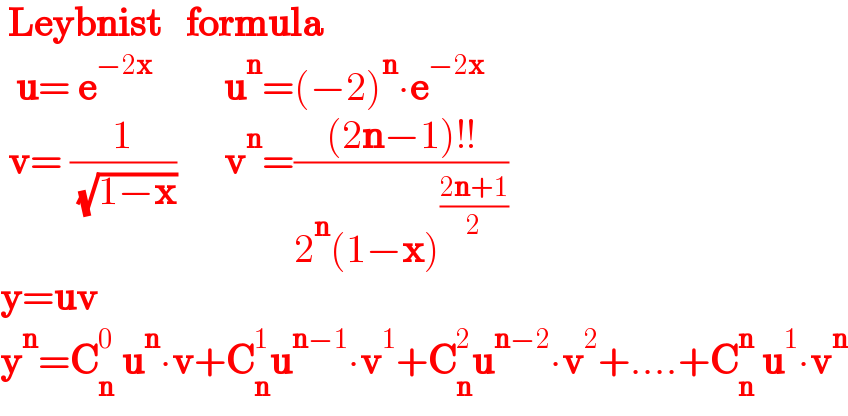
Answered by mathmax by abdo last updated on 10/Feb/21
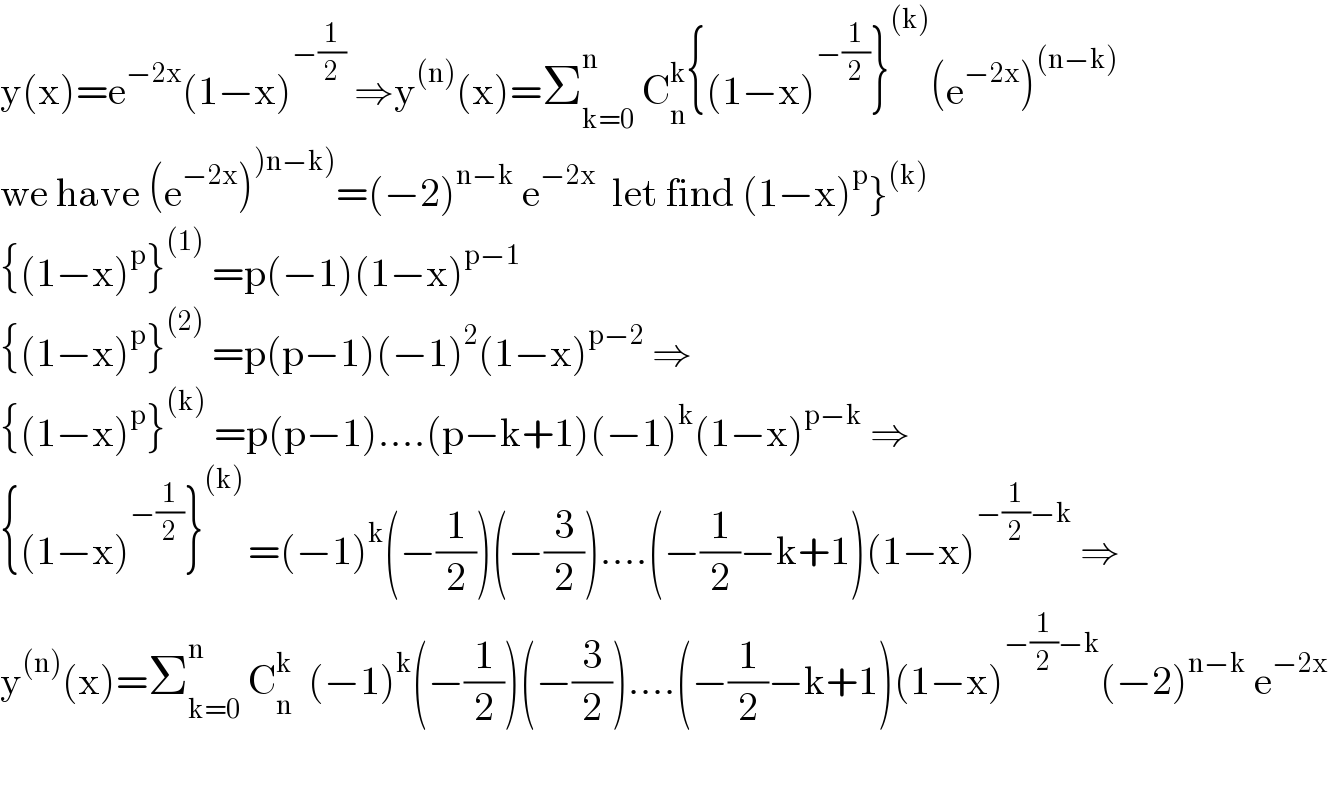
| ||
Question and Answers Forum | ||
Question Number 131887 by Algoritm last updated on 09/Feb/21 | ||
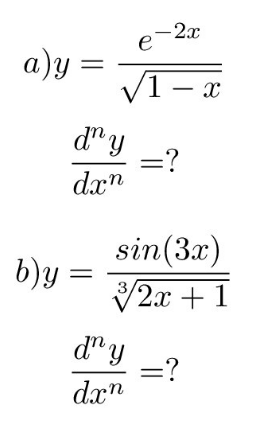 | ||
Answered by SEKRET last updated on 09/Feb/21 | ||
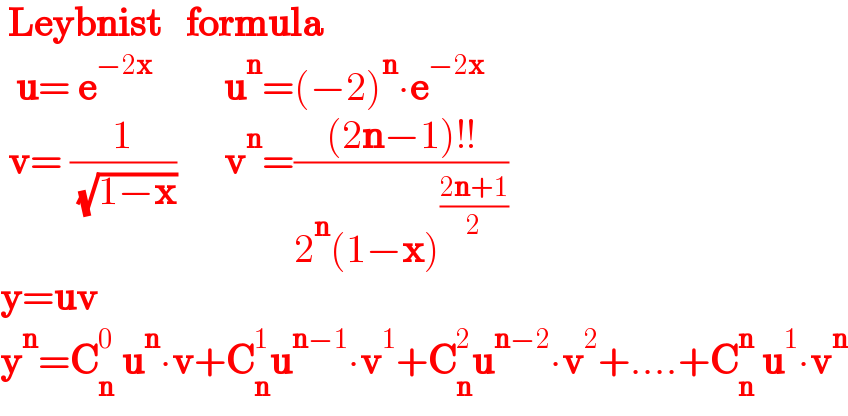 | ||
| ||
Answered by mathmax by abdo last updated on 10/Feb/21 | ||
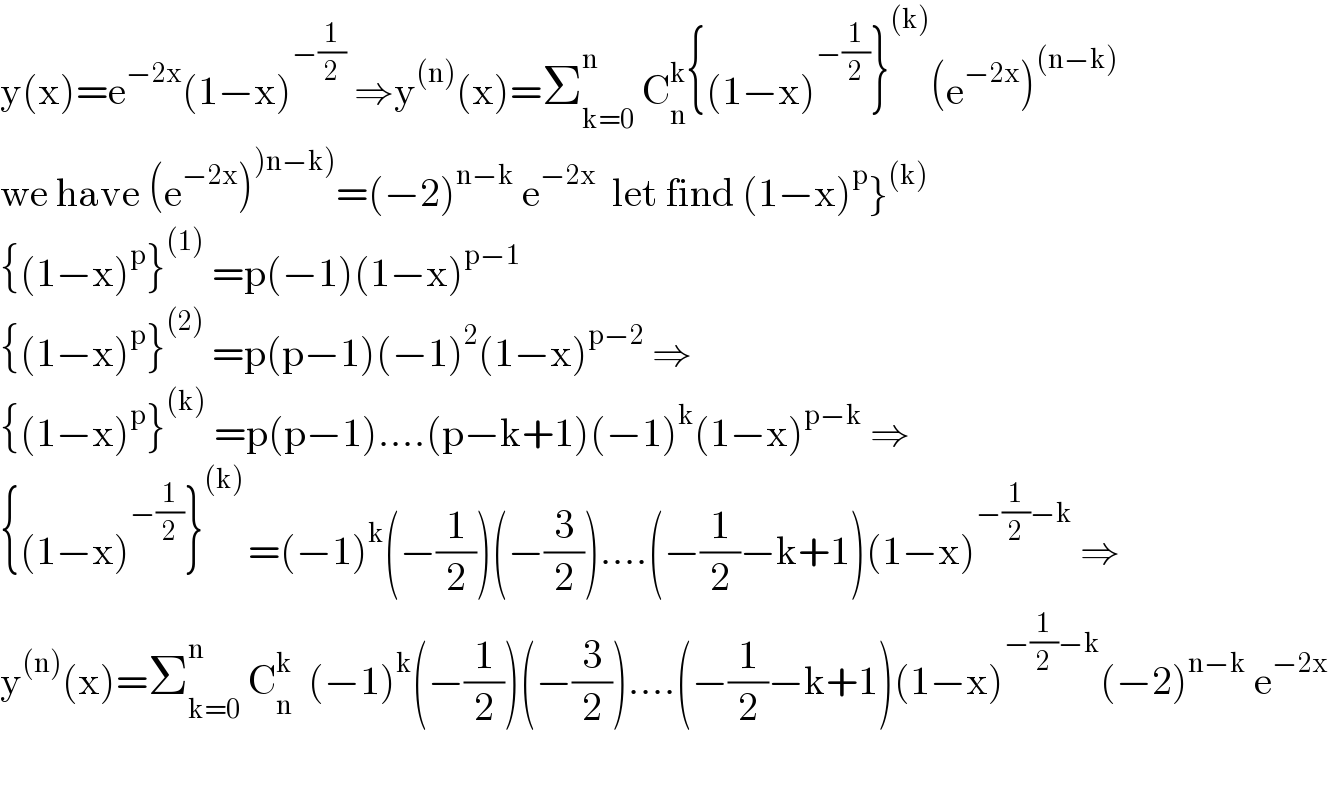 | ||
| ||