
Question and Answers Forum
Question Number 13223 by Tinkutara last updated on 16/May/17
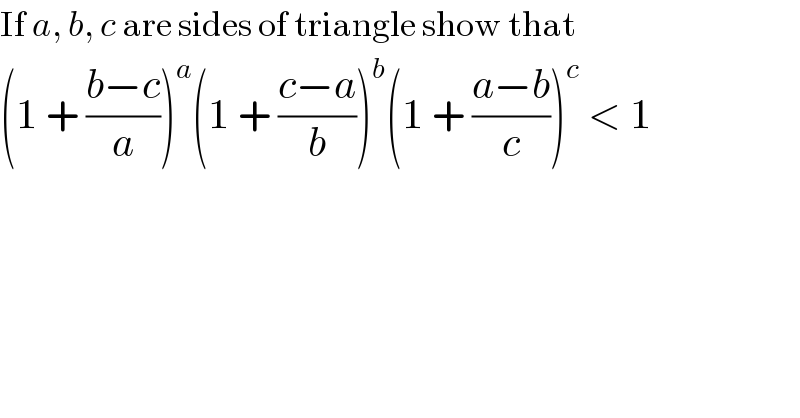
Commented byb.e.h.i.8.3.4.1.7@gmail.com last updated on 17/May/17
![if: a=b=c⇒RHS=1≮LHS=1 1+((b−c)/a)=2×((p−c)/a),1+((c−a)/b)=2((p−a)/b),1+((a−b)/c)=2((p−b)/c) (RHS)_1 =(1+((b−c)/a))(1+((c−a)/b))(1+((a−b)/c))⇒ (RHS)_1 =8×(((p−a)(p−b)(p−c))/(abc))=8×((S^2 /p)/(4RS))= =((2S)/(pR))=((2r)/R)≤1 (according to Euler′s teorem) d^2 =R^2 −2Rr=R(R−2r)≥0⇒R≥2r abc=((2S)/(sinC)).2RsinC=4R.S, S=p.r (1+((b−c)/a))^a (1+((c−a)/b))^b (1+((a−b)/c))^c < (1+((b−c)/a))^(abc) (1+((c−a)/b))^(abc) (1+((a−b)/c))^(abc) = [(1+((b−c)/a))(1+((c−a)/b))(1+((a−b)/c))]^(abc) = =(((2r)/R))^(abc) ≤1^(abc) ≤1 .■](Q13233.png)
| ||
Question and Answers Forum | ||
Question Number 13223 by Tinkutara last updated on 16/May/17 | ||
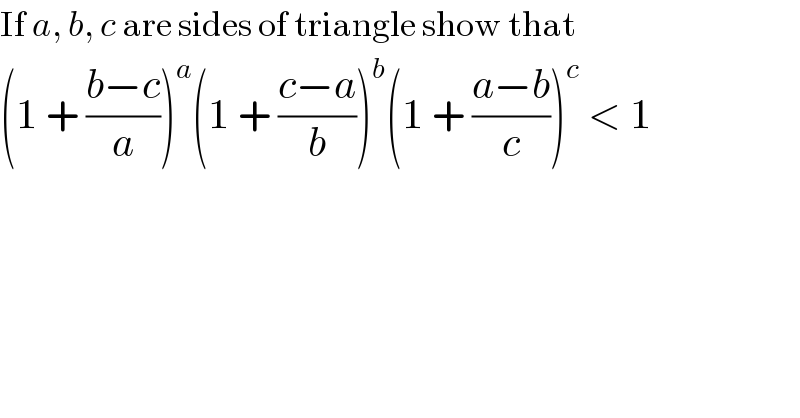 | ||
Commented byb.e.h.i.8.3.4.1.7@gmail.com last updated on 17/May/17 | ||
![if: a=b=c⇒RHS=1≮LHS=1 1+((b−c)/a)=2×((p−c)/a),1+((c−a)/b)=2((p−a)/b),1+((a−b)/c)=2((p−b)/c) (RHS)_1 =(1+((b−c)/a))(1+((c−a)/b))(1+((a−b)/c))⇒ (RHS)_1 =8×(((p−a)(p−b)(p−c))/(abc))=8×((S^2 /p)/(4RS))= =((2S)/(pR))=((2r)/R)≤1 (according to Euler′s teorem) d^2 =R^2 −2Rr=R(R−2r)≥0⇒R≥2r abc=((2S)/(sinC)).2RsinC=4R.S, S=p.r (1+((b−c)/a))^a (1+((c−a)/b))^b (1+((a−b)/c))^c < (1+((b−c)/a))^(abc) (1+((c−a)/b))^(abc) (1+((a−b)/c))^(abc) = [(1+((b−c)/a))(1+((c−a)/b))(1+((a−b)/c))]^(abc) = =(((2r)/R))^(abc) ≤1^(abc) ≤1 .■](Q13233.png) | ||