Question and Answers Forum

All Questions      Topic List

Geometry Questions

Previous in All Question      Next in All Question      

Previous in Geometry      Next in Geometry      

Question Number 13236 by Abbas-Nahi last updated on 17/May/17

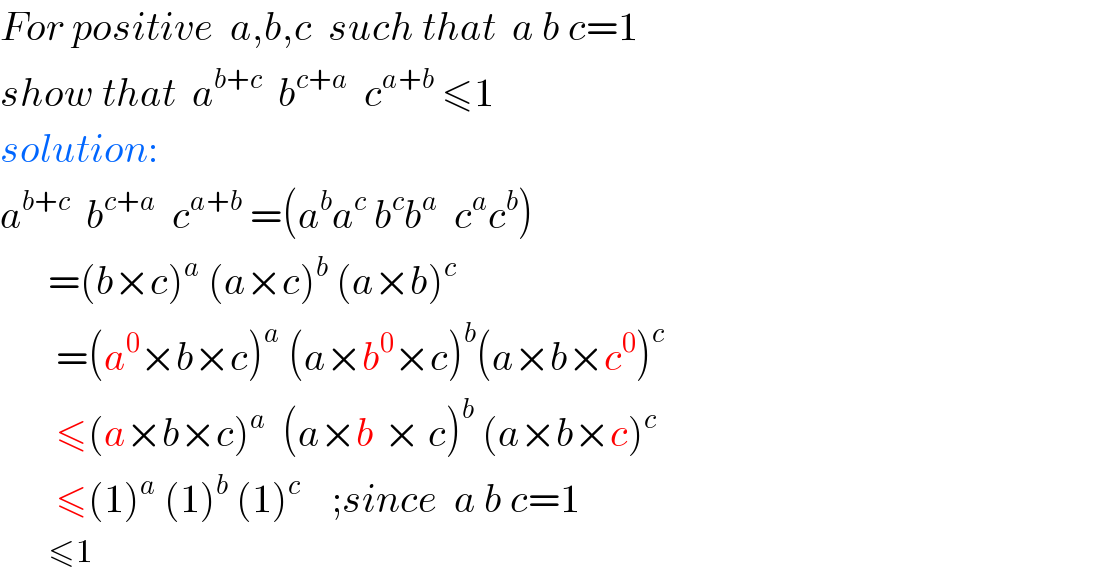
For positive a,b,c such that a b c=1 show that a^(b+c) b^(c+a) c^(a+b) ≤1 solution: a^(b+c) b^(c+a) c^(a+b) =(a^b a^c b^c b^a c^a c^b ) =(b×c)^a (a×c)^b (a×b)^c =(a^0 ×b×c)^a (a×b^0 ×c)^b (a×b×c^0 )^c ≤(a×b×c)^(a ) (a×b^ × c)^b (a×b×c)^c ≤(1)^a (1)^b (1)^c ;since a b c=1 ≤1

$${For}\:{positive}\:\:{a},{b},{c}\:\:{such}\:{that}\:\:{a}\:{b}\:{c}=\mathrm{1} \\ $$$${show}\:{that}\:\:{a}^{{b}+{c}} \:\:{b}^{{c}+{a}} \:\:{c}^{{a}+{b}} \:\leqslant\mathrm{1} \\ $$$${solution}: \\ $$$${a}^{{b}+{c}} \:\:{b}^{{c}+{a}} \:\:{c}^{{a}+{b}} \:=\left({a}^{{b}} {a}^{{c}} \:{b}^{{c}} {b}^{{a}} \:\:{c}^{{a}} {c}^{{b}} \right) \\ $$$$\:\:\:\:\:\:=\left({b}×{c}\right)^{{a}} \:\left({a}×{c}\right)^{{b}} \:\left({a}×{b}\right)^{{c}} \\ $$$$\:\:\:\:\:\:\:=\left({a}^{\mathrm{0}} ×{b}×{c}\right)^{{a}} \:\left({a}×{b}^{\mathrm{0}} ×{c}\right)^{{b}} \left({a}×{b}×{c}^{\mathrm{0}} \right)^{{c}} \\ $$$$\:\:\:\:\:\:\:\leqslant\left({a}×{b}×{c}\right)^{{a}\:\:\:\:} \left({a}×{b}^{} ×\:{c}\right)^{{b}} \:\left({a}×{b}×{c}\right)^{{c}} \\ $$$$\:\:\:\:\:\:\:\leqslant\left(\mathrm{1}\right)^{{a}} \:\left(\mathrm{1}\right)^{{b}} \:\left(\mathrm{1}\right)^{{c}} \:\:\:\:;{since}\:\:{a}\:{b}\:{c}=\mathrm{1} \\ $$$$\:\:\:\:\:\:\:\:\leqslant\mathrm{1} \\ $$

Commented by RasheedSindhi last updated on 17/May/17

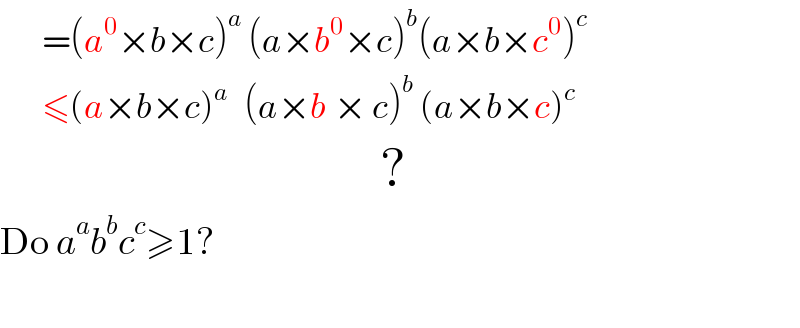
=(a^0 ×b×c)^a (a×b^0 ×c)^b (a×b×c^0 )^c ≤(a×b×c)^(a ) (a×b^ × c)^b (a×b×c)^c ? Do a^a b^b c^c ≥1?

$$\:\:\:\:\:\:\:=\left({a}^{\mathrm{0}} ×{b}×{c}\right)^{{a}} \:\left({a}×{b}^{\mathrm{0}} ×{c}\right)^{{b}} \left({a}×{b}×{c}^{\mathrm{0}} \right)^{{c}} \\ $$$$\:\:\:\:\:\:\:\leqslant\left({a}×{b}×{c}\right)^{{a}\:\:\:\:} \left({a}×{b}^{} ×\:{c}\right)^{{b}} \:\left({a}×{b}×{c}\right)^{{c}} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:? \\ $$$$\mathrm{Do}\:{a}^{{a}} {b}^{{b}} {c}^{{c}} \geqslant\mathrm{1}? \\ $$$$ \\ $$

Commented by mrW1 last updated on 17/May/17

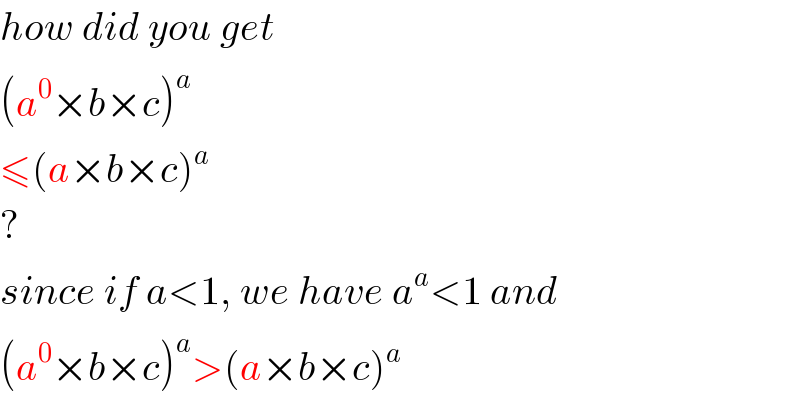
how did you get (a^0 ×b×c)^a ≤(a×b×c)^(a ) ? since if a<1, we have a^a <1 and (a^0 ×b×c)^a >(a×b×c)^(a )

$${how}\:{did}\:{you}\:{get} \\ $$$$\left({a}^{\mathrm{0}} ×{b}×{c}\right)^{{a}} \: \\ $$$$\leqslant\left({a}×{b}×{c}\right)^{{a}\:\:\:\:} \\ $$$$? \\ $$$${since}\:{if}\:{a}<\mathrm{1},\:{we}\:{have}\:{a}^{{a}} <\mathrm{1}\:{and} \\ $$$$\left({a}^{\mathrm{0}} ×{b}×{c}\right)^{{a}} >\left({a}×{b}×{c}\right)^{{a}\:\:\:\:} \\ $$

Commented by Tinkutara last updated on 17/May/17

Yes, your solution is incorrect. Please check it. I now found a better solution. From the given expression a^(b+c) b^(c+a) c^(a+b) = a^(b+c) ((1/(ac)))^(c+a) c^(a+b) [∵ abc = 1] = a^(b+c) a^(−(c+a)) c^(−(c+a)) c^(a+b) = (a^(b+c−c−a) /c^(c+a−a−b) ) = (a^(b−a) /c^(c−b) ) . We can assume that a < b < c as the equation is symmetric. So the numbers are positive and raised to positive powers. So the denominator is greater than the numerator. Hence the above expression is ≤ 1.

$$\mathrm{Yes},\:\mathrm{your}\:\mathrm{solution}\:\mathrm{is}\:\mathrm{incorrect}.\:\mathrm{Please} \\ $$$$\mathrm{check}\:\mathrm{it}.\:\mathrm{I}\:\mathrm{now}\:\mathrm{found}\:\mathrm{a}\:\mathrm{better}\:\mathrm{solution}. \\ $$$$\mathrm{From}\:\mathrm{the}\:\mathrm{given}\:\mathrm{expression} \\ $$$${a}^{{b}+{c}} {b}^{{c}+{a}} {c}^{{a}+{b}} \:=\:{a}^{{b}+{c}} \left(\frac{\mathrm{1}}{{ac}}\right)^{{c}+{a}} {c}^{{a}+{b}} \:\left[\because\:{abc}\:=\:\mathrm{1}\right] \\ $$$$=\:{a}^{{b}+{c}} {a}^{−\left({c}+{a}\right)} {c}^{−\left({c}+{a}\right)} {c}^{{a}+{b}} \\ $$$$=\:\frac{{a}^{{b}+{c}−{c}−{a}} }{{c}^{{c}+{a}−{a}−{b}} }\:=\:\frac{{a}^{{b}−{a}} }{{c}^{{c}−{b}} }\:. \\ $$$$\mathrm{We}\:\mathrm{can}\:\mathrm{assume}\:\mathrm{that}\:{a}\:<\:{b}\:<\:{c}\:\mathrm{as}\:\mathrm{the} \\ $$$$\mathrm{equation}\:\mathrm{is}\:\mathrm{symmetric}. \\ $$$$\mathrm{So}\:\mathrm{the}\:\mathrm{numbers}\:\mathrm{are}\:\mathrm{positive}\:\mathrm{and}\:\mathrm{raised} \\ $$$$\mathrm{to}\:\mathrm{positive}\:\mathrm{powers}. \\ $$$$\mathrm{So}\:\mathrm{the}\:\mathrm{denominator}\:\mathrm{is}\:\mathrm{greater}\:\mathrm{than}\:\mathrm{the} \\ $$$$\mathrm{numerator}. \\ $$$$\mathrm{Hence}\:\mathrm{the}\:\mathrm{above}\:\mathrm{expression}\:\mathrm{is}\:\leqslant\:\mathrm{1}. \\ $$

Commented by RasheedSindhi last updated on 17/May/17

Mr. Tinkutara “So the numbers are positive integers_(−) ” The given codition is only a,b,c>0 ∧ abc=1 Why you′ve assumed a,b,c as integers ?

$$\mathrm{Mr}.\:\mathrm{Tinkutara} \\ $$$$``\mathrm{So}\:\mathrm{the}\:\mathrm{numbers}\:\mathrm{are}\:\mathrm{positive}\:\underset{−} {\mathrm{integers}}'' \\ $$$$\mathrm{The}\:\mathrm{given}\:\mathrm{codition}\:\mathrm{is}\:\mathrm{only} \\ $$$$\:{a},{b},{c}>\mathrm{0}\:\wedge\:{abc}=\mathrm{1} \\ $$$$\mathrm{Why}\:\mathrm{you}'\mathrm{ve}\:\mathrm{assumed}\:{a},{b},{c}\:\mathrm{as} \\ $$$$\boldsymbol{\mathrm{integers}}\:? \\ $$

Commented by Abbas-Nahi last updated on 17/May/17

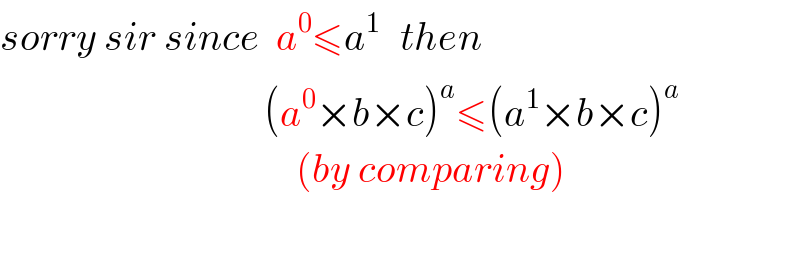
sorry sir since a^0 ≤a^(1 ) then (a^0 ×b×c)^a ≤(a^1 ×b×c)^a (by comparing)

$${sorry}\:{sir}\:{since}\:\:{a}^{\mathrm{0}} \leqslant{a}^{\mathrm{1}\:} \:\:{then} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\left({a}^{\mathrm{0}} ×{b}×{c}\right)^{{a}} \leqslant\left({a}^{\mathrm{1}} ×{b}×{c}\right)^{{a}} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\left({by}\:{comparing}\right) \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\: \\ $$

Commented by Abbas-Nahi last updated on 17/May/17

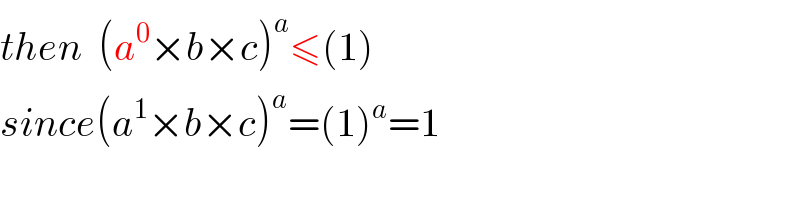
then (a^0 ×b×c)^a ≤(1) since(a^1 ×b×c)^a =(1)^a =1

$${then}\:\:\left({a}^{\mathrm{0}} ×{b}×{c}\right)^{{a}} \leqslant\left(\mathrm{1}\right)\: \\ $$$${since}\left({a}^{\mathrm{1}} ×{b}×{c}\right)^{{a}} =\left(\mathrm{1}\right)^{{a}} =\mathrm{1} \\ $$$$\:\:\: \\ $$

Commented by Abbas-Nahi last updated on 17/May/17

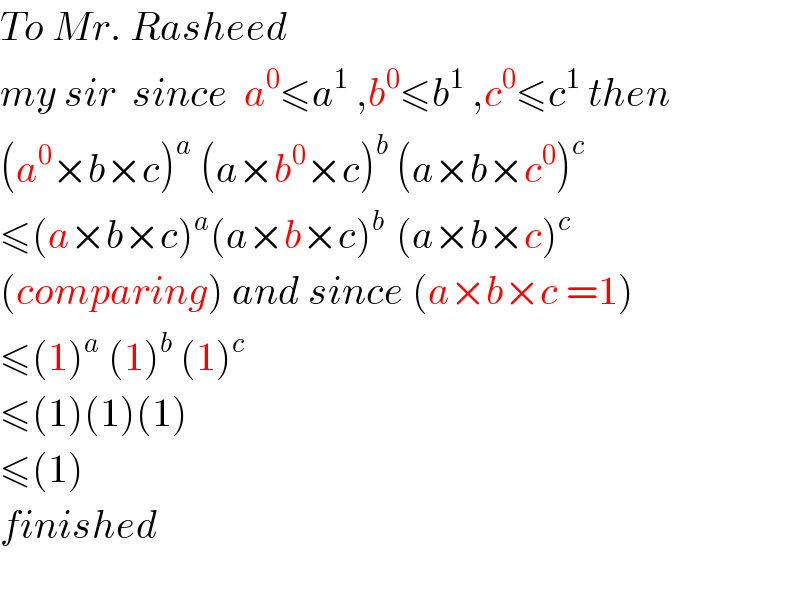
To Mr. Rasheed my sir since a^0 ≤a^1 ,b^0 ≤b^1 ,c^0 ≤c^1 then (a^0 ×b×c)^a (a×b^0 ×c)^b (a×b×c^0 )^c ≤(a×b×c)^a (a×b×c)^(b ) (a×b×c)^c (comparing) and since (a×b×c =1) ≤(1)^a (1)^b (1)^c ≤(1)(1)(1) ≤(1) finished

$${To}\:{Mr}.\:{Rasheed}\: \\ $$$${my}\:{sir}\:\:{since}\:\:{a}^{\mathrm{0}} \leqslant{a}^{\mathrm{1}} \:,{b}^{\mathrm{0}} \leqslant{b}^{\mathrm{1}} \:,{c}^{\mathrm{0}} \leqslant{c}^{\mathrm{1}} \:{then} \\ $$$$\left({a}^{\mathrm{0}} ×{b}×{c}\right)^{{a}} \:\left({a}×{b}^{\mathrm{0}} ×{c}\right)^{{b}} \:\left({a}×{b}×{c}^{\mathrm{0}} \right)^{{c}} \\ $$$$\leqslant\left({a}×{b}×{c}\right)^{{a}} \left({a}×{b}×{c}\right)^{{b}\:} \:\left({a}×{b}×{c}\right)^{{c}} \: \\ $$$$\left({comparing}\right)\:{and}\:{since}\:\left({a}×{b}×{c}\:=\mathrm{1}\right) \\ $$$$\leqslant\left(\mathrm{1}\right)^{{a}} \:\left(\mathrm{1}\right)^{{b}} \:\left(\mathrm{1}\right)^{{c}} \\ $$$$\leqslant\left(\mathrm{1}\right)\left(\mathrm{1}\right)\left(\mathrm{1}\right) \\ $$$$\leqslant\left(\mathrm{1}\right) \\ $$$${finished} \\ $$$$ \\ $$

Commented by RasheedSindhi last updated on 19/May/17

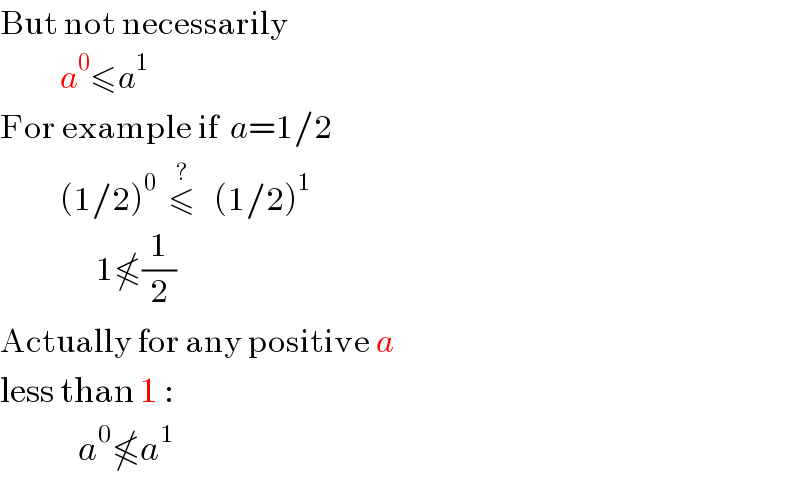
But not necessarily a^0 ≤a^1 For example if a=1/2 (1/2)^0 ≤^(?) (1/2)^1 1≰(1/2) Actually for any positive a less than 1 : a^0 ≰a^1

$$\mathrm{But}\:\mathrm{not}\:\mathrm{necessarily} \\ $$$$\:\:\:\:\:\:\:\:\:\:{a}^{\mathrm{0}} \leqslant{a}^{\mathrm{1}} \\ $$$$\mathrm{For}\:\mathrm{example}\:\mathrm{if}\:\:{a}=\mathrm{1}/\mathrm{2} \\ $$$$\:\:\:\:\:\:\:\:\:\:\left(\mathrm{1}/\mathrm{2}\right)^{\mathrm{0}} \:\:\overset{?} {\leqslant}\:\:\:\left(\mathrm{1}/\mathrm{2}\right)^{\mathrm{1}} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\mathrm{1}\nleqslant\frac{\mathrm{1}}{\mathrm{2}} \\ $$$$\mathrm{Actually}\:\mathrm{for}\:\mathrm{any}\:\mathrm{positive}\:{a} \\ $$$$\mathrm{less}\:\mathrm{than}\:\mathrm{1}\:: \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:{a}^{\mathrm{0}} \nleqslant{a}^{\mathrm{1}} \\ $$

Commented by Abbas-Nahi last updated on 17/May/17

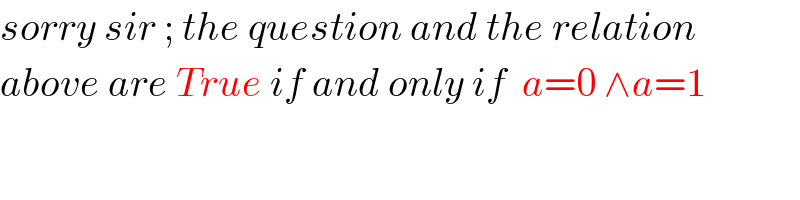
sorry sir ; the question and the relation above are True if and only if a=0 ∧a=1

$${sorry}\:{sir}\:;\:{the}\:{question}\:{and}\:{the}\:{relation} \\ $$$${above}\:{are}\:{True}\:{if}\:{and}\:{only}\:{if}\:\:{a}=\mathrm{0}\:\wedge{a}=\mathrm{1} \\ $$

Commented by mrW1 last updated on 17/May/17

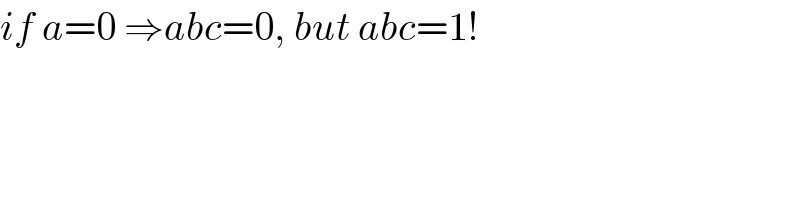
if a=0 ⇒abc=0, but abc=1!

$${if}\:{a}=\mathrm{0}\:\Rightarrow{abc}=\mathrm{0},\:{but}\:{abc}=\mathrm{1}! \\ $$

Commented by Tinkutara last updated on 17/May/17

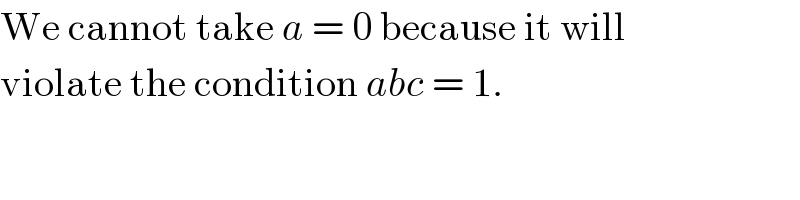
We cannot take a = 0 because it will violate the condition abc = 1.

$$\mathrm{We}\:\mathrm{cannot}\:\mathrm{take}\:{a}\:=\:\mathrm{0}\:\mathrm{because}\:\mathrm{it}\:\mathrm{will} \\ $$$$\mathrm{violate}\:\mathrm{the}\:\mathrm{condition}\:{abc}\:=\:\mathrm{1}. \\ $$

Commented by RasheedSindhi last updated on 17/May/17

a=0 ∧a=1 means a is simultaneously equal to 0 &1? Given condition :abc=1 a,b,c may take any real value other than 0. For example: (1/2)(6)(1/3) To Mr. Abbas pl set a=1/2 , b=6 and c=1/3 in your proof and see! (These values fulfil abc=1)

$${a}=\mathrm{0}\:\wedge{a}=\mathrm{1}\:\mathrm{means}\:{a}\:\mathrm{is}\:\mathrm{simultaneously} \\ $$$$\mathrm{equal}\:\mathrm{to}\:\mathrm{0}\:\&\mathrm{1}? \\ $$$$\mathrm{Given}\:\mathrm{condition}\::{abc}=\mathrm{1} \\ $$$${a},{b},{c}\:\mathrm{may}\:\mathrm{take}\:\mathrm{any}\:\mathrm{real}\:\mathrm{value} \\ $$$$\mathrm{other}\:\mathrm{than}\:\mathrm{0}. \\ $$$$\mathrm{For}\:\mathrm{example}: \\ $$$$\left(\mathrm{1}/\mathrm{2}\right)\left(\mathrm{6}\right)\left(\mathrm{1}/\mathrm{3}\right) \\ $$$$\mathrm{To}\:\mathrm{Mr}.\:\mathrm{Abbas} \\ $$$$\mathrm{pl}\:\mathrm{set}\:{a}=\mathrm{1}/\mathrm{2}\:,\:{b}=\mathrm{6}\:\mathrm{and}\:{c}=\mathrm{1}/\mathrm{3} \\ $$$$\mathrm{in}\:\mathrm{your}\:\mathrm{proof}\:\mathrm{and}\:\mathrm{see}! \\ $$$$\left(\mathrm{These}\:\mathrm{values}\:\mathrm{fulfil}\:{abc}=\mathrm{1}\right) \\ $$

Commented by Tinkutara last updated on 17/May/17

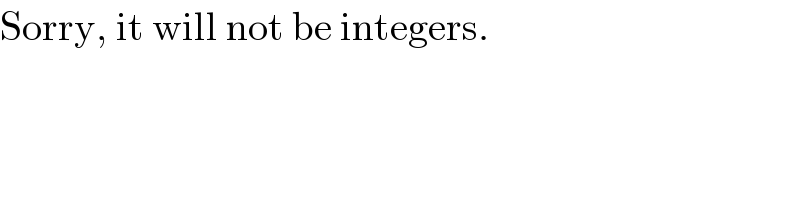
Sorry, it will not be integers.

$$\mathrm{Sorry},\:\mathrm{it}\:\mathrm{will}\:\mathrm{not}\:\mathrm{be}\:\mathrm{integers}. \\ $$

Commented by prakash jain last updated on 18/May/17

To Tinkutara Your argument that positive numbers raised to +ve power hence denominator is greater than numerator is not valid. In general a>b,x>0,y>0 does not imply a^x >b^y

$$\mathrm{To}\:\mathrm{Tinkutara} \\ $$$$\mathrm{Your}\:\mathrm{argument}\:\mathrm{that}\:\mathrm{positive} \\ $$$$\mathrm{numbers}\:\mathrm{raised}\:\mathrm{to}\:+\mathrm{ve}\:\mathrm{power} \\ $$$$\mathrm{hence}\:\mathrm{denominator}\:\mathrm{is}\:\mathrm{greater} \\ $$$$\mathrm{than}\:\mathrm{numerator}\:\mathrm{is}\:\mathrm{not}\:\mathrm{valid}. \\ $$$$\mathrm{In}\:\mathrm{general} \\ $$$${a}>{b},{x}>\mathrm{0},{y}>\mathrm{0} \\ $$$$\mathrm{does}\:\mathrm{not}\:\mathrm{imply} \\ $$$${a}^{{x}} >{b}^{{y}} \\ $$

Commented by Tinkutara last updated on 19/May/17

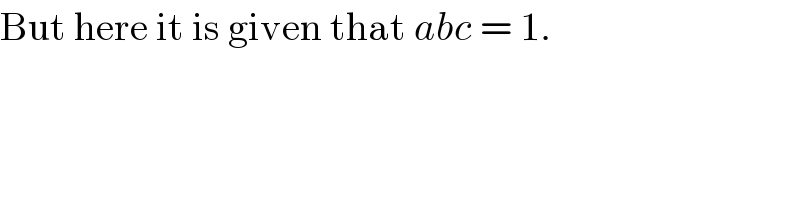
But here it is given that abc = 1.

$$\mathrm{But}\:\mathrm{here}\:\mathrm{it}\:\mathrm{is}\:\mathrm{given}\:\mathrm{that}\:{abc}\:=\:\mathrm{1}. \\ $$

Commented by prakash jain last updated on 19/May/17

I added a clarification that the readers know that an additional condition is required a<c is not sufficient. MrW1 added in another post that a≤1 and c≥1 which is an additional condition.

$$\mathrm{I}\:\mathrm{added}\:\mathrm{a}\:\mathrm{clarification} \\ $$$$\mathrm{that}\:\mathrm{the}\:\mathrm{readers}\:\mathrm{know}\:\mathrm{that}\:\mathrm{an} \\ $$$$\mathrm{additional}\:\mathrm{condition}\:\mathrm{is}\:\mathrm{required} \\ $$$${a}<{c}\:\mathrm{is}\:\mathrm{not}\:\mathrm{sufficient}. \\ $$$$\mathrm{MrW1}\:\mathrm{added}\:\mathrm{in}\:\mathrm{another}\:\mathrm{post} \\ $$$$\mathrm{that}\:{a}\leqslant\mathrm{1}\:\mathrm{and}\:{c}\geqslant\mathrm{1}\:\mathrm{which}\:\mathrm{is}\:\mathrm{an} \\ $$$$\mathrm{additional}\:\mathrm{condition}. \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com