Question and Answers Forum

All Questions      Topic List

Others Questions

Previous in All Question      Next in All Question      

Previous in Others      Next in Others      

Question Number 13302 by tawa tawa last updated on 17/May/17

(a) A body of mass m initially at rest at a point O on a smooth horizontal surface. A horizontal force F is applied to the body and caused it to move in a straight line accross the surface. The magnitude of F is given by F = (1/(s + α)), Where S is the distance of the body from O and α is the positive constant. If v is the speed of the body at any moment, Show that S = α (e^((1/2)mv^2 ) − 1). (b) If F = 15s + 4 and m = 1 kg and the body is initially at rest at point O. Determine, (i) v when s = 2m (ii) s when v = 8m/s

$$\left(\mathrm{a}\right) \\ $$$$\mathrm{A}\:\mathrm{body}\:\mathrm{of}\:\mathrm{mass}\:\mathrm{m}\:\mathrm{initially}\:\mathrm{at}\:\mathrm{rest}\:\mathrm{at}\:\mathrm{a}\:\mathrm{point}\:\mathrm{O}\:\mathrm{on}\:\mathrm{a}\:\mathrm{smooth}\:\mathrm{horizontal}\:\mathrm{surface}. \\ $$$$\mathrm{A}\:\mathrm{horizontal}\:\mathrm{force}\:\mathrm{F}\:\mathrm{is}\:\mathrm{applied}\:\mathrm{to}\:\mathrm{the}\:\mathrm{body}\:\mathrm{and}\:\mathrm{caused}\:\mathrm{it}\:\mathrm{to}\:\mathrm{move}\:\mathrm{in}\:\mathrm{a}\:\mathrm{straight} \\ $$$$\mathrm{line}\:\mathrm{accross}\:\mathrm{the}\:\mathrm{surface}.\:\mathrm{The}\:\mathrm{magnitude}\:\mathrm{of}\:\mathrm{F}\:\mathrm{is}\:\mathrm{given}\:\mathrm{by}\:\mathrm{F}\:=\:\frac{\mathrm{1}}{\mathrm{s}\:+\:\alpha},\:\mathrm{Where}\:\mathrm{S}\:\mathrm{is} \\ $$$$\mathrm{the}\:\mathrm{distance}\:\mathrm{of}\:\mathrm{the}\:\mathrm{body}\:\mathrm{from}\:\mathrm{O}\:\mathrm{and}\:\alpha\:\mathrm{is}\:\mathrm{the}\:\mathrm{positive}\:\mathrm{constant}.\:\mathrm{If}\:\mathrm{v}\:\mathrm{is}\:\mathrm{the}\:\mathrm{speed} \\ $$$$\mathrm{of}\:\mathrm{the}\:\mathrm{body}\:\mathrm{at}\:\mathrm{any}\:\mathrm{moment},\:\mathrm{Show}\:\mathrm{that}\:\mathrm{S}\:=\:\alpha\:\left(\mathrm{e}^{\frac{\mathrm{1}}{\mathrm{2}}\mathrm{mv}^{\mathrm{2}} } −\:\mathrm{1}\right).\: \\ $$$$\left(\mathrm{b}\right) \\ $$$$\mathrm{If}\:\:\mathrm{F}\:=\:\mathrm{15s}\:+\:\mathrm{4}\:\:\mathrm{and}\:\:\mathrm{m}\:=\:\mathrm{1}\:\mathrm{kg}\:\:\mathrm{and}\:\:\mathrm{the}\:\mathrm{body}\:\mathrm{is}\:\mathrm{initially}\:\mathrm{at}\:\mathrm{rest}\:\mathrm{at}\:\mathrm{point}\:\mathrm{O}. \\ $$$$\mathrm{Determine}, \\ $$$$\left(\mathrm{i}\right)\:\:\mathrm{v}\:\:\mathrm{when}\:\:\mathrm{s}\:=\:\mathrm{2m}\:\:\:\:\:\:\:\:\left(\mathrm{ii}\right)\:\mathrm{s}\:\:\mathrm{when}\:\:\mathrm{v}\:=\:\mathrm{8m}/\mathrm{s} \\ $$

Answered by mrW1 last updated on 17/May/17

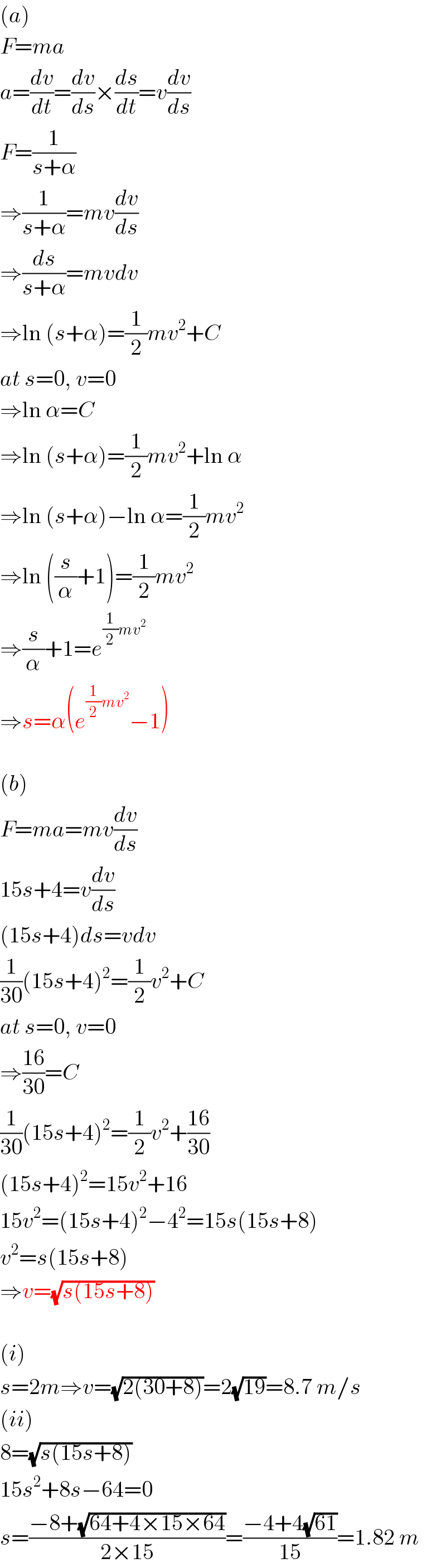
(a) F=ma a=(dv/dt)=(dv/ds)×(ds/dt)=v(dv/ds) F=(1/(s+α)) ⇒(1/(s+α))=mv(dv/ds) ⇒(ds/(s+α))=mvdv ⇒ln (s+α)=(1/2)mv^2 +C at s=0, v=0 ⇒ln α=C ⇒ln (s+α)=(1/2)mv^2 +ln α ⇒ln (s+α)−ln α=(1/2)mv^2 ⇒ln ((s/α)+1)=(1/2)mv^2 ⇒(s/α)+1=e^((1/2)mv^2 ) ⇒s=α(e^((1/2)mv^2 ) −1) (b) F=ma=mv(dv/ds) 15s+4=v(dv/ds) (15s+4)ds=vdv (1/(30))(15s+4)^2 =(1/2)v^2 +C at s=0, v=0 ⇒((16)/(30))=C (1/(30))(15s+4)^2 =(1/2)v^2 +((16)/(30)) (15s+4)^2 =15v^2 +16 15v^2 =(15s+4)^2 −4^2 =15s(15s+8) v^2 =s(15s+8) ⇒v=(√(s(15s+8))) (i) s=2m⇒v=(√(2(30+8)))=2(√(19))=8.7 m/s (ii) 8=(√(s(15s+8))) 15s^2 +8s−64=0 s=((−8+(√(64+4×15×64)))/(2×15))=((−4+4(√(61)))/(15))=1.82 m

$$\left({a}\right) \\ $$$${F}={ma} \\ $$$${a}=\frac{{dv}}{{dt}}=\frac{{dv}}{{ds}}×\frac{{ds}}{{dt}}={v}\frac{{dv}}{{ds}} \\ $$$${F}=\frac{\mathrm{1}}{{s}+\alpha} \\ $$$$\Rightarrow\frac{\mathrm{1}}{{s}+\alpha}={mv}\frac{{dv}}{{ds}} \\ $$$$\Rightarrow\frac{{ds}}{{s}+\alpha}={mvdv} \\ $$$$\Rightarrow\mathrm{ln}\:\left({s}+\alpha\right)=\frac{\mathrm{1}}{\mathrm{2}}{mv}^{\mathrm{2}} +{C} \\ $$$${at}\:{s}=\mathrm{0},\:{v}=\mathrm{0} \\ $$$$\Rightarrow\mathrm{ln}\:\alpha={C} \\ $$$$\Rightarrow\mathrm{ln}\:\left({s}+\alpha\right)=\frac{\mathrm{1}}{\mathrm{2}}{mv}^{\mathrm{2}} +\mathrm{ln}\:\alpha \\ $$$$\Rightarrow\mathrm{ln}\:\left({s}+\alpha\right)−\mathrm{ln}\:\alpha=\frac{\mathrm{1}}{\mathrm{2}}{mv}^{\mathrm{2}} \\ $$$$\Rightarrow\mathrm{ln}\:\left(\frac{{s}}{\alpha}+\mathrm{1}\right)=\frac{\mathrm{1}}{\mathrm{2}}{mv}^{\mathrm{2}} \\ $$$$\Rightarrow\frac{{s}}{\alpha}+\mathrm{1}={e}^{\frac{\mathrm{1}}{\mathrm{2}}{mv}^{\mathrm{2}} } \\ $$$$\Rightarrow{s}=\alpha\left({e}^{\frac{\mathrm{1}}{\mathrm{2}}{mv}^{\mathrm{2}} } −\mathrm{1}\right) \\ $$$$ \\ $$$$\left({b}\right) \\ $$$${F}={ma}={mv}\frac{{dv}}{{ds}} \\ $$$$\mathrm{15}{s}+\mathrm{4}={v}\frac{{dv}}{{ds}} \\ $$$$\left(\mathrm{15}{s}+\mathrm{4}\right){ds}={vdv} \\ $$$$\frac{\mathrm{1}}{\mathrm{30}}\left(\mathrm{15}{s}+\mathrm{4}\right)^{\mathrm{2}} =\frac{\mathrm{1}}{\mathrm{2}}{v}^{\mathrm{2}} +{C} \\ $$$${at}\:{s}=\mathrm{0},\:{v}=\mathrm{0} \\ $$$$\Rightarrow\frac{\mathrm{16}}{\mathrm{30}}={C} \\ $$$$\frac{\mathrm{1}}{\mathrm{30}}\left(\mathrm{15}{s}+\mathrm{4}\right)^{\mathrm{2}} =\frac{\mathrm{1}}{\mathrm{2}}{v}^{\mathrm{2}} +\frac{\mathrm{16}}{\mathrm{30}} \\ $$$$\left(\mathrm{15}{s}+\mathrm{4}\right)^{\mathrm{2}} =\mathrm{15}{v}^{\mathrm{2}} +\mathrm{16} \\ $$$$\mathrm{15}{v}^{\mathrm{2}} =\left(\mathrm{15}{s}+\mathrm{4}\right)^{\mathrm{2}} −\mathrm{4}^{\mathrm{2}} =\mathrm{15}{s}\left(\mathrm{15}{s}+\mathrm{8}\right) \\ $$$${v}^{\mathrm{2}} ={s}\left(\mathrm{15}{s}+\mathrm{8}\right) \\ $$$$\Rightarrow{v}=\sqrt{{s}\left(\mathrm{15}{s}+\mathrm{8}\right)} \\ $$$$ \\ $$$$\left({i}\right) \\ $$$${s}=\mathrm{2}{m}\Rightarrow{v}=\sqrt{\mathrm{2}\left(\mathrm{30}+\mathrm{8}\right)}=\mathrm{2}\sqrt{\mathrm{19}}=\mathrm{8}.\mathrm{7}\:{m}/{s} \\ $$$$\left({ii}\right) \\ $$$$\mathrm{8}=\sqrt{{s}\left(\mathrm{15}{s}+\mathrm{8}\right)} \\ $$$$\mathrm{15}{s}^{\mathrm{2}} +\mathrm{8}{s}−\mathrm{64}=\mathrm{0} \\ $$$${s}=\frac{−\mathrm{8}+\sqrt{\mathrm{64}+\mathrm{4}×\mathrm{15}×\mathrm{64}}}{\mathrm{2}×\mathrm{15}}=\frac{−\mathrm{4}+\mathrm{4}\sqrt{\mathrm{61}}}{\mathrm{15}}=\mathrm{1}.\mathrm{82}\:{m} \\ $$

Commented by tawa tawa last updated on 18/May/17

Wow, God bless you sir. I really appreciate.

$$\mathrm{Wow},\:\mathrm{God}\:\mathrm{bless}\:\mathrm{you}\:\mathrm{sir}.\:\mathrm{I}\:\mathrm{really}\:\mathrm{appreciate}. \\ $$

Answered by ajfour last updated on 18/May/17

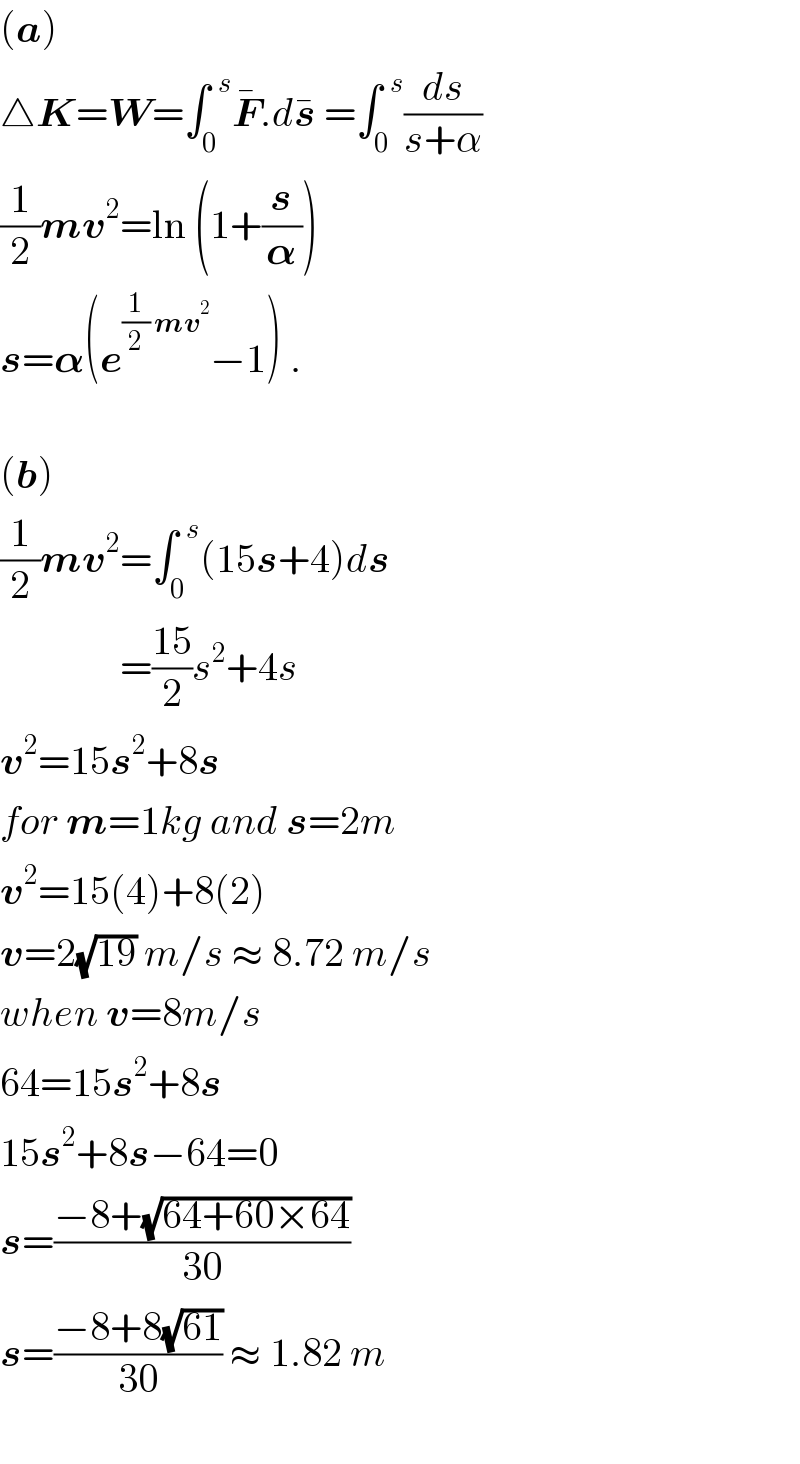
(a) △K=W=∫_0 ^( s) F^� .ds^� =∫_0 ^( s) (ds/(s+α)) (1/2)mv^2 =ln (1+(s/𝛂)) s=𝛂(e^((1/2) mv^2 ) −1) . (b) (1/2)mv^2 =∫_0 ^( s) (15s+4)ds =((15)/2)s^2 +4s v^2 =15s^2 +8s for m=1kg and s=2m v^2 =15(4)+8(2) v=2(√(19)) m/s ≈ 8.72 m/s when v=8m/s 64=15s^2 +8s 15s^2 +8s−64=0 s=((−8+(√(64+60×64)))/(30)) s=((−8+8(√(61)))/(30)) ≈ 1.82 m

$$\left(\boldsymbol{{a}}\right) \\ $$$$\bigtriangleup\boldsymbol{{K}}=\boldsymbol{{W}}=\int_{\mathrm{0}} ^{\:\:{s}} \bar {\boldsymbol{{F}}}.{d}\bar {\boldsymbol{{s}}}\:=\int_{\mathrm{0}} ^{\:\:{s}} \frac{{ds}}{{s}+\alpha} \\ $$$$\frac{\mathrm{1}}{\mathrm{2}}\boldsymbol{{mv}}^{\mathrm{2}} =\mathrm{ln}\:\left(\mathrm{1}+\frac{\boldsymbol{{s}}}{\boldsymbol{\alpha}}\right) \\ $$$$\boldsymbol{{s}}=\boldsymbol{\alpha}\left(\boldsymbol{{e}}^{\frac{\mathrm{1}}{\mathrm{2}}\:\boldsymbol{{mv}}^{\mathrm{2}} } −\mathrm{1}\right)\:. \\ $$$$ \\ $$$$\left(\boldsymbol{{b}}\right) \\ $$$$\frac{\mathrm{1}}{\mathrm{2}}\boldsymbol{{mv}}^{\mathrm{2}} =\int_{\mathrm{0}} ^{\:\:{s}} \left(\mathrm{15}\boldsymbol{{s}}+\mathrm{4}\right){d}\boldsymbol{{s}} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:=\frac{\mathrm{15}}{\mathrm{2}}{s}^{\mathrm{2}} +\mathrm{4}{s} \\ $$$$\boldsymbol{{v}}^{\mathrm{2}} =\mathrm{15}\boldsymbol{{s}}^{\mathrm{2}} +\mathrm{8}\boldsymbol{{s}} \\ $$$${for}\:\boldsymbol{{m}}=\mathrm{1}{kg}\:{and}\:\boldsymbol{{s}}=\mathrm{2}{m} \\ $$$$\boldsymbol{{v}}^{\mathrm{2}} =\mathrm{15}\left(\mathrm{4}\right)+\mathrm{8}\left(\mathrm{2}\right) \\ $$$$\boldsymbol{{v}}=\mathrm{2}\sqrt{\mathrm{19}}\:{m}/{s}\:\approx\:\mathrm{8}.\mathrm{72}\:{m}/{s} \\ $$$${when}\:\boldsymbol{{v}}=\mathrm{8}{m}/{s} \\ $$$$\mathrm{64}=\mathrm{15}\boldsymbol{{s}}^{\mathrm{2}} +\mathrm{8}\boldsymbol{{s}} \\ $$$$\mathrm{15}\boldsymbol{{s}}^{\mathrm{2}} +\mathrm{8}\boldsymbol{{s}}−\mathrm{64}=\mathrm{0} \\ $$$$\boldsymbol{{s}}=\frac{−\mathrm{8}+\sqrt{\mathrm{64}+\mathrm{60}×\mathrm{64}}}{\mathrm{30}} \\ $$$$\boldsymbol{{s}}=\frac{−\mathrm{8}+\mathrm{8}\sqrt{\mathrm{61}}}{\mathrm{30}}\:\approx\:\mathrm{1}.\mathrm{82}\:{m} \\ $$$$\: \\ $$

Commented by tawa tawa last updated on 18/May/17

God bless you sir. i really appreciate.

$$\mathrm{God}\:\mathrm{bless}\:\mathrm{you}\:\mathrm{sir}.\:\mathrm{i}\:\mathrm{really}\:\mathrm{appreciate}. \\ $$

Commented by mrW1 last updated on 18/May/17

wonderful!

$${wonderful}! \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com