Question and Answers Forum

All Questions      Topic List

Integration Questions

Previous in All Question      Next in All Question      

Previous in Integration      Next in Integration      

Question Number 133027 by Engr_Jidda last updated on 18/Feb/21

$${\stackrel{2}{\int }}_0{x}^5{(8-x^3)}^{\frac{1}{3}}dx$$

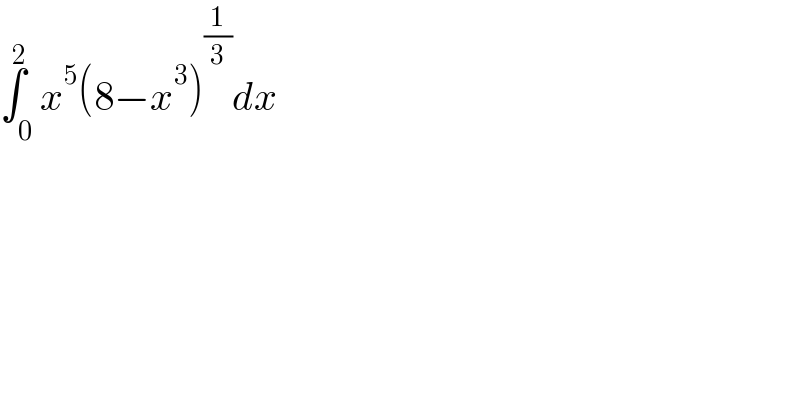
Answered by Olaf last updated on 18/Feb/21

$$\mathrm{\Omega }={\int }_0^2{x}^5{(8-x^3)}^{\frac{1}{3}}dx$$$$\mathrm{\Omega }={\int }_0^2(-\frac{1}{4}{x}^3)[-4x^2{(8-x^3)}^{\frac{1}{3}}]dx$$$$\mathrm{\Omega }={\left[(-\frac{1}{4}{x}^3){(8-x^3)}^{\frac{4}{3}}\right]}_0^2-{\int }_0^2(-\frac{3}{4}{x}^2){(8-x^3)}^{\frac{4}{3}}dx$$$$\mathrm{\Omega }=\frac{3}{4}{\int }_0^2{x}^2{(8-x^3)}^{\frac{4}{3}}dx$$$$\mathrm{\Omega }=\frac{3}{4}{\int }_0^2(-\frac{1}{7})[-7x^2{(8-x^3)}^{\frac{4}{3}}]dx$$$$\mathrm{\Omega }=-\frac{3}{4\times 7}{\left[{(8-x^3)}^{\frac{7}{3}}\right]}_0^2$$$$\mathrm{\Omega }=\frac{3\times 8^{\frac{7}{3}}}{4\times 7}=\frac{3\times 2^7}{7\times 2^2}=\frac{96}{7}$$

Commented by Engr_Jidda last updated on 22/Feb/21

$$thankyousir$$

Answered by liberty last updated on 18/Feb/21

$$\mathrm{I}={\underset{0}{\int }}^2{\mathrm{x}}^3.{\mathrm{x}}^2\sqrt[3]{8-{\mathrm{x}}^3}\mathrm{dx}$$$$\mathrm{change}\mathrm{of}\mathrm{variable}$$$$\mathrm{put}{\mathrm{u}}^3=8-{\mathrm{x}}^3\mathrm{where}\{\begin{array}{l}\mathrm{for}\mathrm{x}=2\to \mathrm{u}=0\\ \mathrm{for}\mathrm{x}=0\to \mathrm{u}=2\end{array}$$$${\mathrm{x}}^2\mathrm{dx}=-{\mathrm{u}}^2\mathrm{du}$$$$\mathrm{I}=\underset{2}{\stackrel{0}{\int }}(8-{\mathrm{u}}^3)\mathrm{u}(-{\mathrm{u}}^2\mathrm{du})$$$$\mathrm{I}=\underset{2}{\stackrel{0}{\int }}({\mathrm{u}}^6-{8\mathrm{u}}^3)\mathrm{du}$$$${\mathrm{I}{=\frac{{\mathrm{u}}^7}{7}-{2\mathrm{u}}^4]}_2^0={\mathrm{u}}^4(\frac{{\mathrm{u}}^3}{7}-2)]}_2^0$$$$\mathrm{I}=-16(\frac{8}{7}-2)=-16(-\frac{6}{7})$$$$\mathrm{I}=\frac{96}{7}\approx 13.714286$$

Commented by liberty last updated on 18/Feb/21

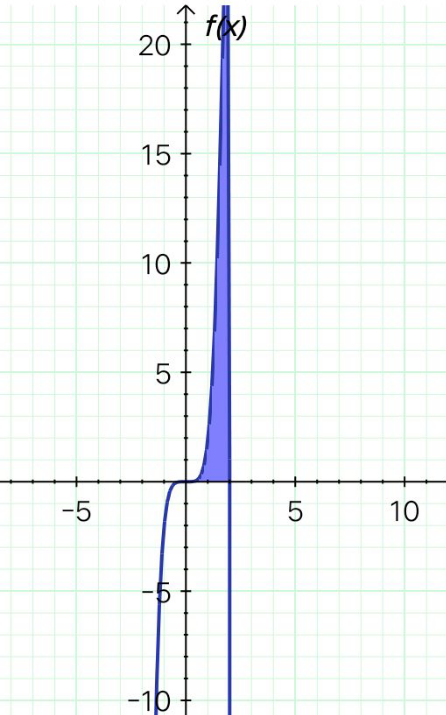
Commented by EDWIN88 last updated on 18/Feb/21

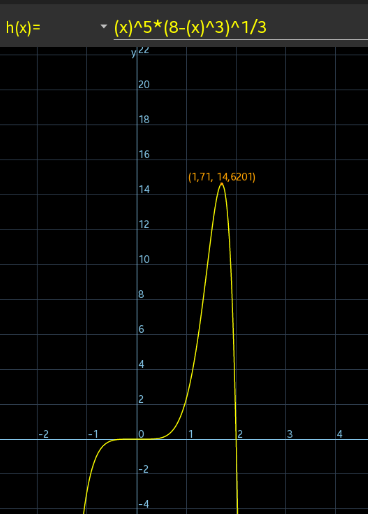
Commented by Engr_Jidda last updated on 22/Feb/21

$$thankyousir$$

Answered by Dwaipayan Shikari last updated on 18/Feb/21

$${\int }_0^2{x}^5{(8-x^3)}^{\frac{1}{3}}dx{x}^3=8u\Rightarrow 3x^2=8\frac{du}{dx}$$$$=\frac{16}{3}{\int }_0^{1}8u{(1-u)}^{\frac{1}{3}}du=\frac{128}{3}.\frac{\mathrm{\Gamma }\left(2\right)\mathrm{\Gamma }\left(\frac{4}{3}\right)}{\mathrm{\Gamma }\left(\frac{10}{3}\right)}=128.\frac{\mathrm{\Gamma }\left(\frac{4}{3}\right)}{7\mathrm{\Gamma }\left(\frac{7}{3}\right)}$$$$=\frac{128}{7}.\frac{3}{4}=\frac{96}{7}$$

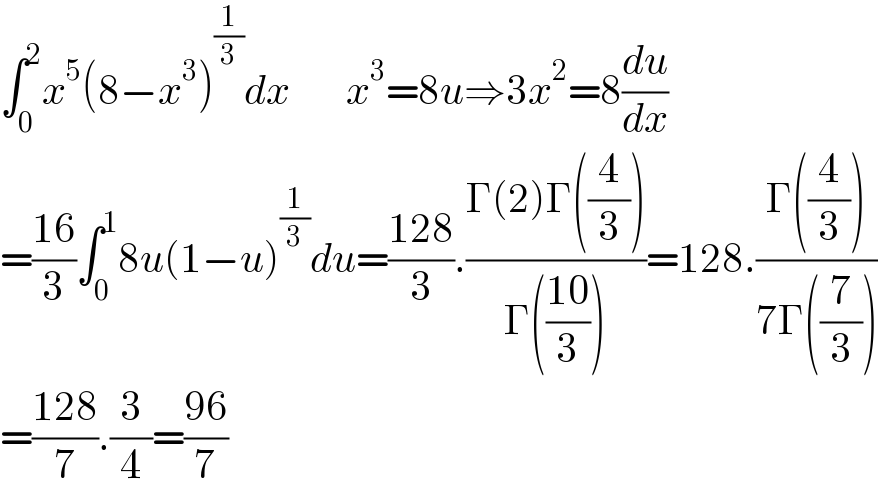
Commented by Engr_Jidda last updated on 22/Feb/21

$$thankyousir$$

Answered by mathmax by abdo last updated on 20/Feb/21

$$\mathrm{\Phi }={\int }_0^2{\mathrm{x}}^5{(8-{\mathrm{x}}^3)}^{\frac{1}{3}}\mathrm{dx}\Rightarrow \mathrm{\Phi }{=}_{\mathrm{x}=2\mathrm{t}}{\int }_0^1{2}^5{\mathrm{t}}^5{(8-{8\mathrm{t}}^3)}^{\frac{1}{3}}2\mathrm{dt}$$$$=2^6.2{\int }_0^1{\mathrm{t}}^5{(1-{\mathrm{t}}^3)}^{\frac{1}{3}}\mathrm{dt}{=}_{{\mathrm{t}}^3=\mathrm{u}}{2}^7{\int }_0^1{\mathrm{u}}^{\frac{5}{3}}{(1-\mathrm{u})}^{\frac{1}{3}}\frac{1}{3}{\mathrm{u}}^{\frac{1}{3}-1}\mathrm{du}$$$$=\frac{2^7}{3}{\int }_0^1{\mathrm{u}}^{2-1}{(1-\mathrm{u})}^{\frac{4}{3}-1}=\frac{2^7}{3}\mathrm{B}(2,\frac{4}{3})=\frac{2^7}{3}.\frac{\mathrm{\Gamma }\left(2\right).\mathrm{\Gamma }\left(\frac{4}{3}\right)}{\mathrm{\Gamma }(2+\frac{4}{3})}$$$$=\frac{2^7}{3}\frac{\mathrm{\Gamma }\left(\frac{4}{3}\right)}{\mathrm{\Gamma }\left(\frac{10}{3}\right)}$$

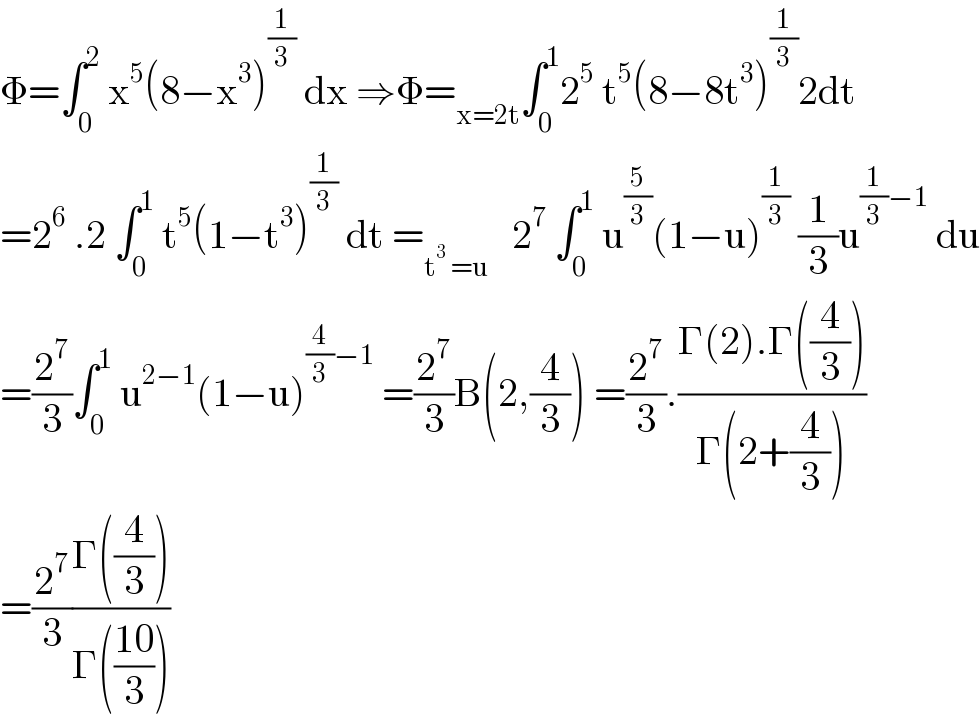
Commented by Engr_Jidda last updated on 22/Feb/21

$$thankyousir$$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com