
Question and Answers Forum
Question Number 133056 by mr W last updated on 19/Feb/21
Commented by mr W last updated on 18/Feb/21

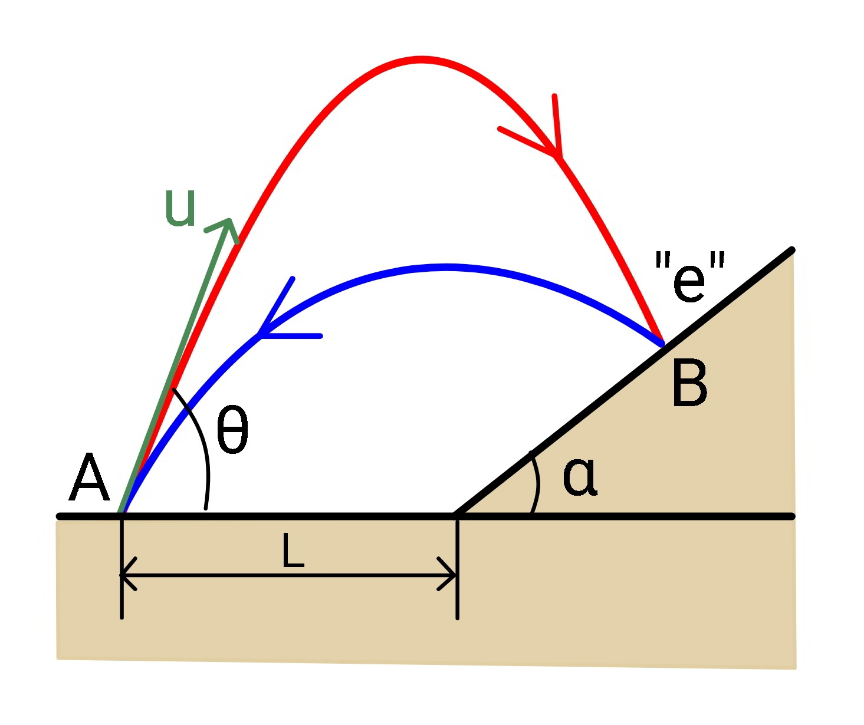
$${a}\:{ball}\:{is}\:{thrown}\:{from}\:{point}\:{A}\:{with} \\ $$$${speed}\:\boldsymbol{{u}}\:{at}\:{an}\:{angle}\:\boldsymbol{\theta}\:{to}\:{horizontal} \\ $$$${and}\:{strikes}\:{at}\:{a}\:{point}\:{on}\:{the}\: \\ $$$${inclined}\:{plane}\:{and}\:{returns}\:{back}\:{to} \\ $$$${point}\:{A}.\:{the}\:{restitution}\:{coefficient}\: \\ $$$${of}\:{the}\:{collision}\:{is}\:\boldsymbol{{e}}. \\ $$$${find}\:{the}\:{speed}\:\boldsymbol{{u}}\:{in}\:{terms}\:{of}\:\boldsymbol{\theta}\:{and} \\ $$$${determine}\:{the}\:{minimum}\:{speed}\:\boldsymbol{{u}}_{\boldsymbol{{min}}} \\ $$$${the}\:{ball}\:{must}\:{have}. \\ $$
Commented by liberty last updated on 18/Feb/21
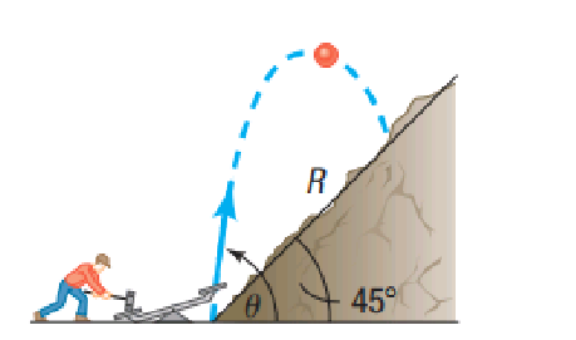
Commented by liberty last updated on 18/Feb/21
$$ \\ $$$$\mathrm{exactly}\:\mathrm{the}\:\mathrm{same}.\:\mathrm{hahaha} \\ $$
Commented by mr W last updated on 18/Feb/21

$${hahaha},\:{if}\:{you}\:{mean}\:{they}\:{are}\:{exactly} \\ $$$${the}\:{same},\:{then}\:{you}\:{seem}\:{not}\:{to}\:{have} \\ $$$${read}\:{both}\:{questions}\:\boldsymbol{{exactly}}.\: \\ $$
Commented by liberty last updated on 18/Feb/21

$$ \\ $$$$\mathrm{yes}\:\mathrm{maybe}\:\mathrm{the}\:\mathrm{question}\:\mathrm{is} \\ $$$$\mathrm{different}.\:\:\mathrm{the}\:\mathrm{exact}\:\mathrm{same}\:\mathrm{is}\:\mathrm{the}\: \\ $$$$\mathrm{picture} \\ $$
Commented by liberty last updated on 18/Feb/21

$$\mathrm{hahahaha} \\ $$
Answered by mr W last updated on 19/Feb/21
Commented by EDWIN88 last updated on 20/Feb/21

$$\mathrm{amazing} \\ $$
Commented by mr W last updated on 20/Feb/21
![B(L+s cos α, s sin α) with s=ξL, ξ≥0 from A to B: t=((L+s cos α)/(u cos θ))=((L(1+ξ cos α))/(u cos θ)) s sin α=((L(1+ξ cos α))/(u cos θ))[u sin θ−(g/2)×((L(1+ξ cos α))/(u cos θ))] ξ sin α=(1+ξ cos α)[tan θ−((gL(1+ξ cos α)(1+tan^2 θ))/(2u^2 ))] let λ=((gL)/(2u^2 )) ξ sin α=(1+ξ cos α)[tan θ−λ(1+ξ cos α)(1+tan^2 θ)] λ(1+ξ cos α)tan^2 θ−tan θ+((ξ sin α+λ(1+ξ cos α)^2 )/((1+ξ cos α)))=0 ⇒tan θ=((1±(√(1−4λ[ξ sin α+λ(1+ξ cos α)^2 ])))/(2λ(1+ξ cos α))) at point B: (see Q132102 for more detail) U=coming speed V=leaving speed (→) U_x =u cos θ U_y =−u sin θ+g×((L(1+ξ cos α))/(u cos θ)) (↓) U_y =u[−sin θ+((2λ(1+ξ cos α))/(cos θ))] let e′=1+e V_x =(e′ sin^2 α−1)U_x +e′ sin α cos α U_y (←) V_x =u[−e′ sin α sin (θ−α)−cos θ+((λe′(1+ξ cos α) sin 2α)/(cos θ))] V_y =e′ sin α cos α U_x +(e′ cos^2 α−1)U_y (↑) V_y =u[−e′ cos α sin (θ−α)+sin θ+((2λ(e′ cos^2 α−1)(1+ξ cos α))/(cos θ))] from B to A: t=((L(1+ξ cos α))/(u[−e′ sin α sin (θ−α)−cos θ+((λe′(1+ξ cos α) sin 2α)/(cos θ))])) ((tu)/L)=η=((1+ξ cos α)/(−e′ sin α sin (θ−α)−cos θ+((λe′(1+ξ cos α) sin 2α)/(cos θ)))) s sin α=t{−u[−e′ cos α sin (θ−α)+sin θ+((2λ(e′ cos^2 α−1)(1+ξ cos α))/(cos θ))]+(1/2)gt} ξ sin α=((tu)/L)[e′ cos α sin (θ−α)−sin θ−((2λ(e′ cos^2 α−1)(1+ξ cos α))/(cos θ))+((gL)/(2u^2 ))×((tu)/L)] ⇒ξ sin α=η[e′ cos α sin (θ−α)−sin θ−((2λ(e′ cos^2 α−1)(1+ξ cos α))/(cos θ))+λη] ...(I) for a given λ we can find ξ through (I).](Q133132.png)
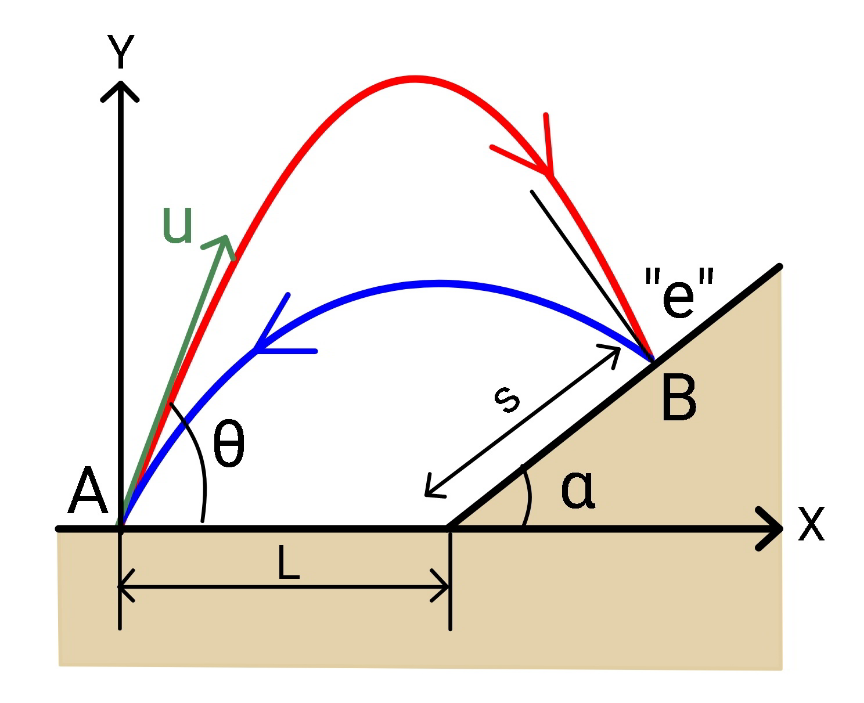
$${B}\left({L}+{s}\:\mathrm{cos}\:\alpha,\:{s}\:\mathrm{sin}\:\alpha\right) \\ $$$${with}\:{s}=\xi{L},\:\xi\geqslant\mathrm{0} \\ $$$$ \\ $$$$\boldsymbol{{from}}\:\boldsymbol{{A}}\:\boldsymbol{{to}}\:\boldsymbol{{B}}: \\ $$$${t}=\frac{{L}+{s}\:\mathrm{cos}\:\alpha}{{u}\:\mathrm{cos}\:\theta}=\frac{{L}\left(\mathrm{1}+\xi\:\mathrm{cos}\:\alpha\right)}{{u}\:\mathrm{cos}\:\theta} \\ $$$${s}\:\mathrm{sin}\:\alpha=\frac{{L}\left(\mathrm{1}+\xi\:\mathrm{cos}\:\alpha\right)}{{u}\:\mathrm{cos}\:\theta}\left[{u}\:\mathrm{sin}\:\theta−\frac{{g}}{\mathrm{2}}×\frac{{L}\left(\mathrm{1}+\xi\:\mathrm{cos}\:\alpha\right)}{{u}\:\mathrm{cos}\:\theta}\right] \\ $$$$\xi\:\mathrm{sin}\:\alpha=\left(\mathrm{1}+\xi\:\mathrm{cos}\:\alpha\right)\left[\mathrm{tan}\:\theta−\frac{{gL}\left(\mathrm{1}+\xi\:\mathrm{cos}\:\alpha\right)\left(\mathrm{1}+\mathrm{tan}^{\mathrm{2}} \:\theta\right)}{\mathrm{2}{u}^{\mathrm{2}} }\right] \\ $$$${let}\:\lambda=\frac{{gL}}{\mathrm{2}{u}^{\mathrm{2}} } \\ $$$$\xi\:\mathrm{sin}\:\alpha=\left(\mathrm{1}+\xi\:\mathrm{cos}\:\alpha\right)\left[\mathrm{tan}\:\theta−\lambda\left(\mathrm{1}+\xi\:\mathrm{cos}\:\alpha\right)\left(\mathrm{1}+\mathrm{tan}^{\mathrm{2}} \:\theta\right)\right] \\ $$$$\lambda\left(\mathrm{1}+\xi\:\mathrm{cos}\:\alpha\right)\mathrm{tan}^{\mathrm{2}} \:\theta−\mathrm{tan}\:\theta+\frac{\xi\:\mathrm{sin}\:\alpha+\lambda\left(\mathrm{1}+\xi\:\mathrm{cos}\:\alpha\right)^{\mathrm{2}} }{\left(\mathrm{1}+\xi\:\mathrm{cos}\:\alpha\right)}=\mathrm{0} \\ $$$$\Rightarrow\mathrm{tan}\:\theta=\frac{\mathrm{1}\pm\sqrt{\mathrm{1}−\mathrm{4}\lambda\left[\xi\:\mathrm{sin}\:\alpha+\lambda\left(\mathrm{1}+\xi\:\mathrm{cos}\:\alpha\right)^{\mathrm{2}} \right]}}{\mathrm{2}\lambda\left(\mathrm{1}+\xi\:\mathrm{cos}\:\alpha\right)} \\ $$$$ \\ $$$$\boldsymbol{{at}}\:\boldsymbol{{point}}\:\boldsymbol{{B}}: \\ $$$$\left({see}\:{Q}\mathrm{132102}\:{for}\:{more}\:{detail}\right) \\ $$$${U}={coming}\:{speed} \\ $$$${V}={leaving}\:{speed} \\ $$$$ \\ $$$$\left(\rightarrow\right)\:{U}_{{x}} ={u}\:\mathrm{cos}\:\theta \\ $$$${U}_{{y}} =−{u}\:\mathrm{sin}\:\theta+{g}×\frac{{L}\left(\mathrm{1}+\xi\:\mathrm{cos}\:\alpha\right)}{{u}\:\mathrm{cos}\:\theta} \\ $$$$\left(\downarrow\right)\:{U}_{{y}} ={u}\left[−\mathrm{sin}\:\theta+\frac{\mathrm{2}\lambda\left(\mathrm{1}+\xi\:\mathrm{cos}\:\alpha\right)}{\mathrm{cos}\:\theta}\right] \\ $$$${let}\:{e}'=\mathrm{1}+{e} \\ $$$${V}_{{x}} =\left({e}'\:\mathrm{sin}^{\mathrm{2}} \:\alpha−\mathrm{1}\right){U}_{{x}} +{e}'\:\mathrm{sin}\:\alpha\:\mathrm{cos}\:\alpha\:{U}_{{y}} \\ $$$$\left(\leftarrow\right)\:{V}_{{x}} ={u}\left[−{e}'\:\mathrm{sin}\:\alpha\:\mathrm{sin}\:\left(\theta−\alpha\right)−\mathrm{cos}\:\theta+\frac{\lambda{e}'\left(\mathrm{1}+\xi\:\mathrm{cos}\:\alpha\right)\:\mathrm{sin}\:\mathrm{2}\alpha}{\mathrm{cos}\:\theta}\right] \\ $$$${V}_{{y}} ={e}'\:\mathrm{sin}\:\alpha\:\mathrm{cos}\:\alpha\:{U}_{{x}} +\left({e}'\:\mathrm{cos}^{\mathrm{2}} \:\alpha−\mathrm{1}\right){U}_{{y}} \\ $$$$\left(\uparrow\right)\:{V}_{{y}} ={u}\left[−{e}'\:\mathrm{cos}\:\alpha\:\mathrm{sin}\:\left(\theta−\alpha\right)+\mathrm{sin}\:\theta+\frac{\mathrm{2}\lambda\left({e}'\:\mathrm{cos}^{\mathrm{2}} \:\alpha−\mathrm{1}\right)\left(\mathrm{1}+\xi\:\mathrm{cos}\:\alpha\right)}{\mathrm{cos}\:\theta}\right] \\ $$$$ \\ $$$$\boldsymbol{{from}}\:\boldsymbol{{B}}\:\boldsymbol{{to}}\:\boldsymbol{{A}}: \\ $$$${t}=\frac{{L}\left(\mathrm{1}+\xi\:\mathrm{cos}\:\alpha\right)}{{u}\left[−{e}'\:\mathrm{sin}\:\alpha\:\mathrm{sin}\:\left(\theta−\alpha\right)−\mathrm{cos}\:\theta+\frac{\lambda{e}'\left(\mathrm{1}+\xi\:\mathrm{cos}\:\alpha\right)\:\mathrm{sin}\:\mathrm{2}\alpha}{\mathrm{cos}\:\theta}\right]} \\ $$$$\frac{{tu}}{{L}}=\eta=\frac{\mathrm{1}+\xi\:\mathrm{cos}\:\alpha}{−{e}'\:\mathrm{sin}\:\alpha\:\mathrm{sin}\:\left(\theta−\alpha\right)−\mathrm{cos}\:\theta+\frac{\lambda{e}'\left(\mathrm{1}+\xi\:\mathrm{cos}\:\alpha\right)\:\mathrm{sin}\:\mathrm{2}\alpha}{\mathrm{cos}\:\theta}} \\ $$$${s}\:\mathrm{sin}\:\alpha={t}\left\{−{u}\left[−{e}'\:\mathrm{cos}\:\alpha\:\mathrm{sin}\:\left(\theta−\alpha\right)+\mathrm{sin}\:\theta+\frac{\mathrm{2}\lambda\left({e}'\:\mathrm{cos}^{\mathrm{2}} \:\alpha−\mathrm{1}\right)\left(\mathrm{1}+\xi\:\mathrm{cos}\:\alpha\right)}{\mathrm{cos}\:\theta}\right]+\frac{\mathrm{1}}{\mathrm{2}}{gt}\right\} \\ $$$$\xi\:\mathrm{sin}\:\alpha=\frac{{tu}}{{L}}\left[{e}'\:\mathrm{cos}\:\alpha\:\mathrm{sin}\:\left(\theta−\alpha\right)−\mathrm{sin}\:\theta−\frac{\mathrm{2}\lambda\left({e}'\:\mathrm{cos}^{\mathrm{2}} \:\alpha−\mathrm{1}\right)\left(\mathrm{1}+\xi\:\mathrm{cos}\:\alpha\right)}{\mathrm{cos}\:\theta}+\frac{{gL}}{\mathrm{2}{u}^{\mathrm{2}} }×\frac{{tu}}{{L}}\right] \\ $$$$\Rightarrow\xi\:\mathrm{sin}\:\alpha=\eta\left[{e}'\:\mathrm{cos}\:\alpha\:\mathrm{sin}\:\left(\theta−\alpha\right)−\mathrm{sin}\:\theta−\frac{\mathrm{2}\lambda\left({e}'\:\mathrm{cos}^{\mathrm{2}} \:\alpha−\mathrm{1}\right)\left(\mathrm{1}+\xi\:\mathrm{cos}\:\alpha\right)}{\mathrm{cos}\:\theta}+\lambda\eta\right]\:\:\:...\left({I}\right) \\ $$$$ \\ $$$${for}\:{a}\:{given}\:\lambda\:{we}\:{can}\:{find}\:\xi\:{through}\:\left({I}\right). \\ $$
Commented by mr W last updated on 20/Feb/21
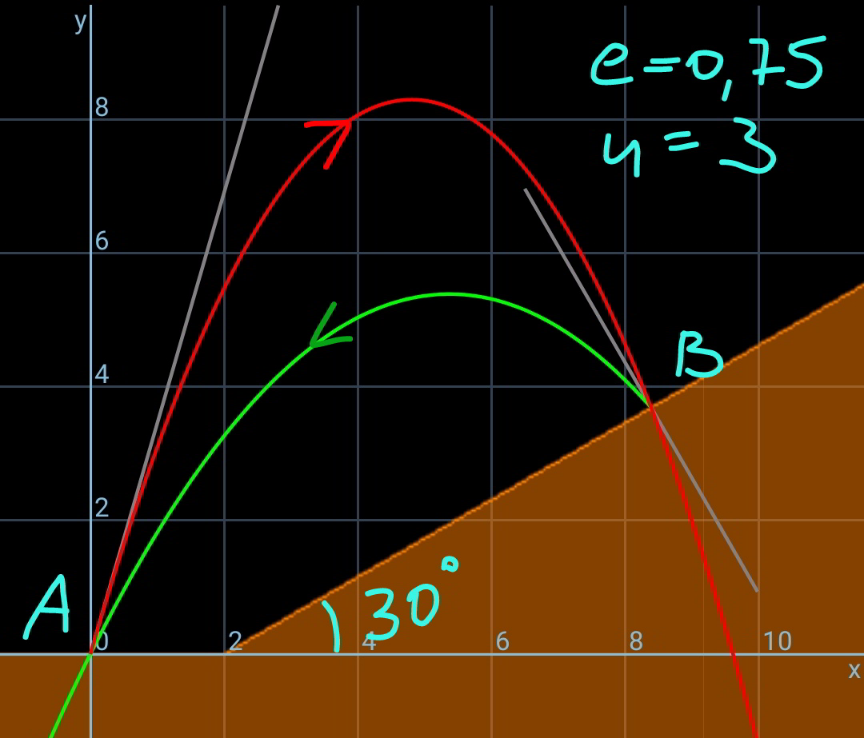
Commented by mr W last updated on 20/Feb/21
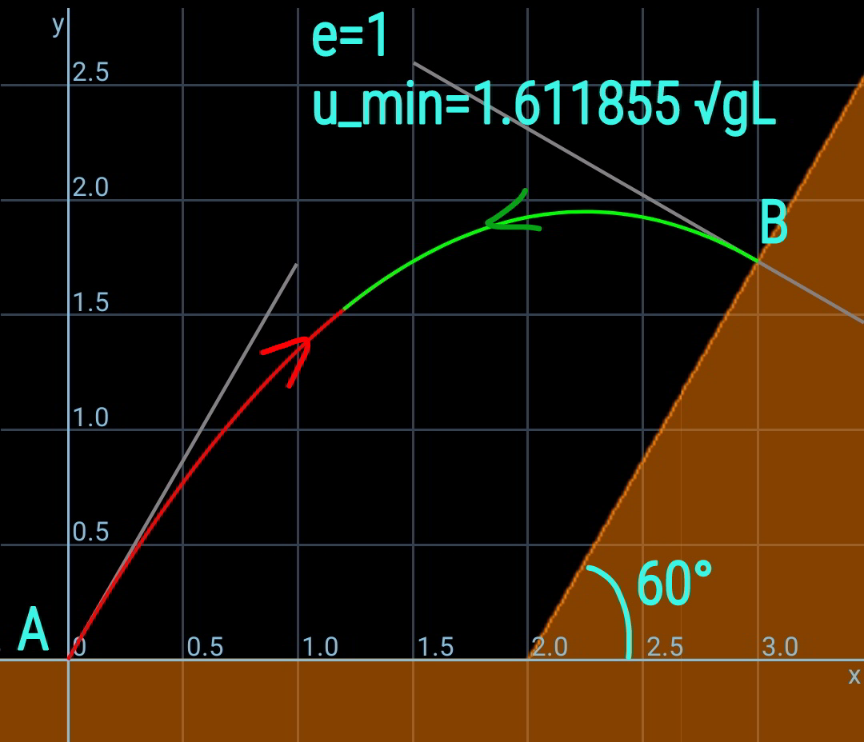
Commented by mr W last updated on 19/Feb/21
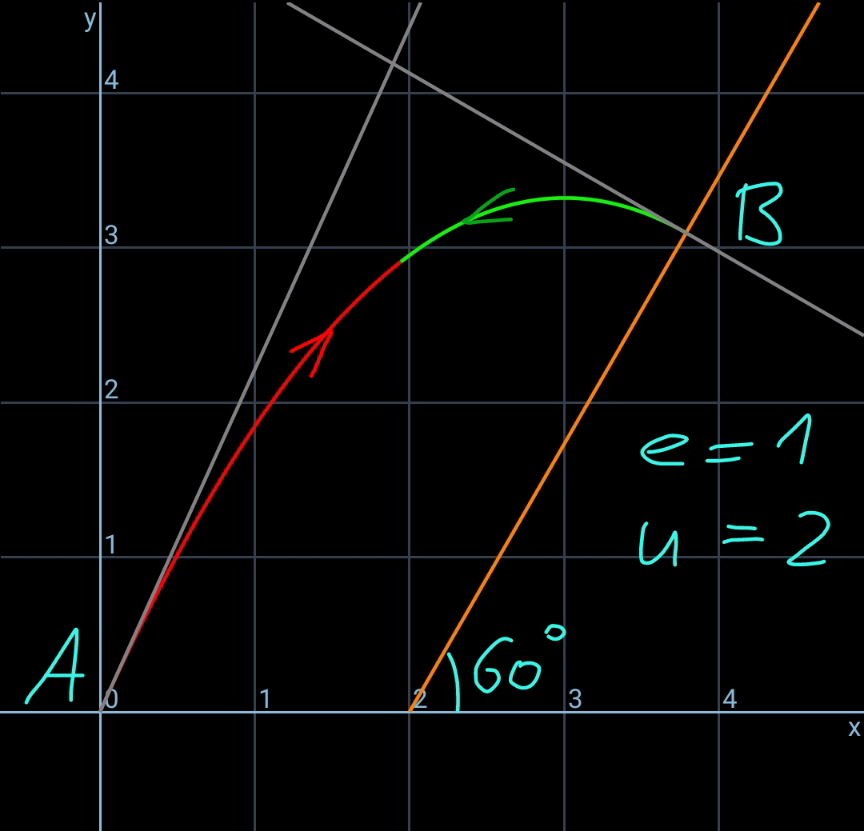
Commented by mr W last updated on 19/Feb/21
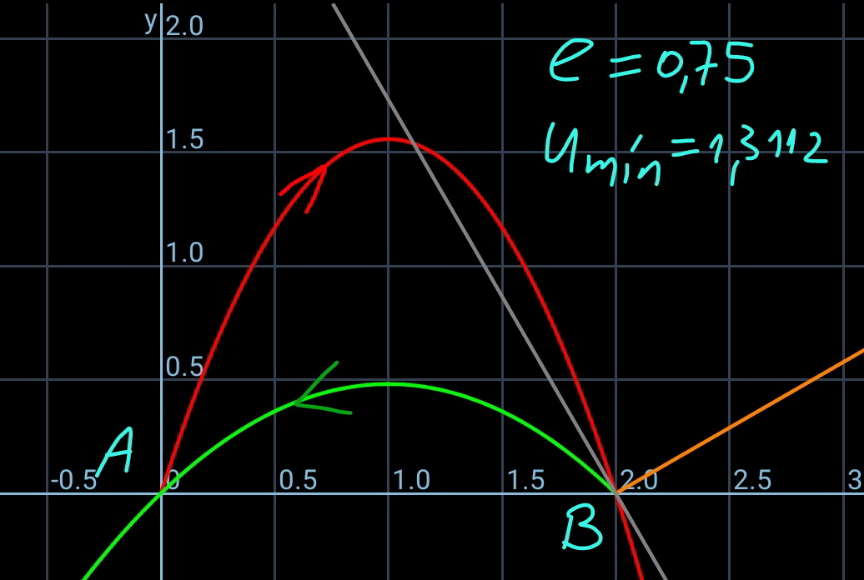
Commented by mr W last updated on 19/Feb/21
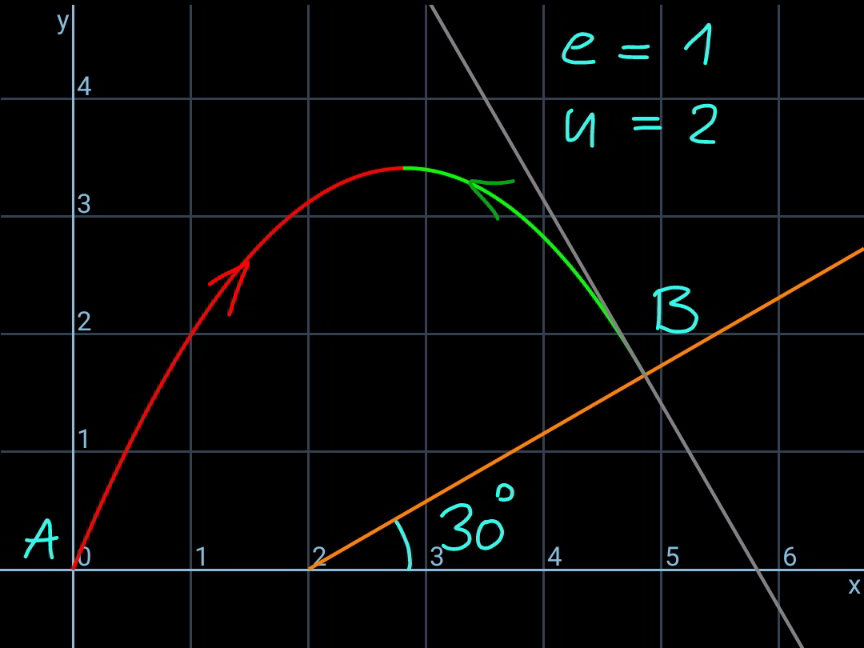
Commented by mr W last updated on 19/Feb/21
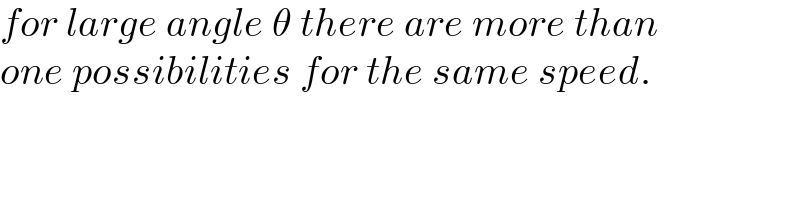
$${for}\:{large}\:{angle}\:\theta\:{there}\:{are}\:{more}\:{than} \\ $$$${one}\:{possibilities}\:{for}\:{the}\:{same}\:{speed}. \\ $$
Commented by mr W last updated on 20/Feb/21
Commented by mr W last updated on 20/Feb/21
Commented by mr W last updated on 20/Feb/21
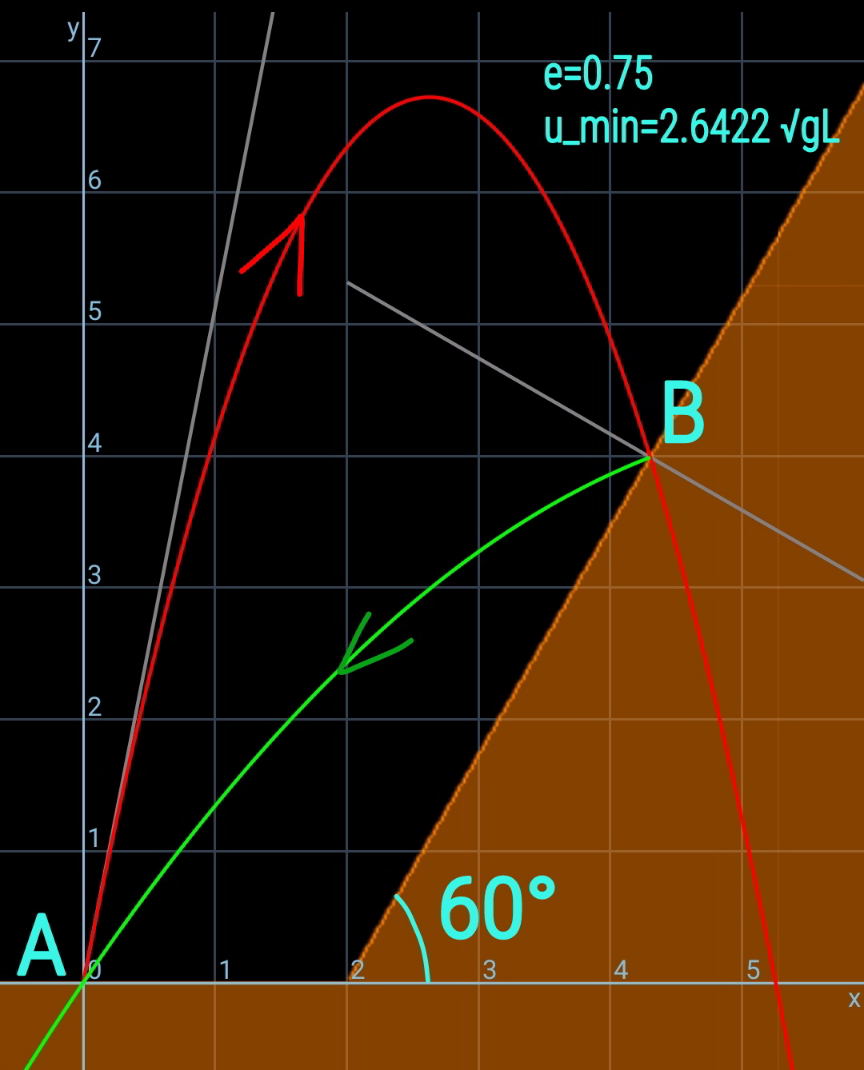
Commented by mr W last updated on 19/Feb/21
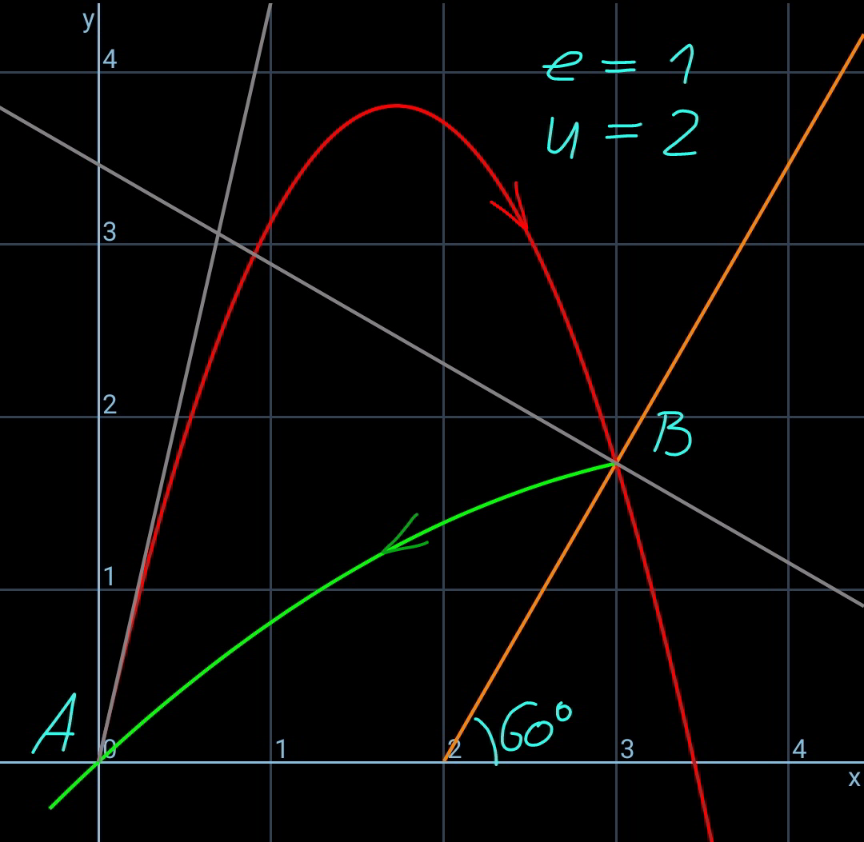
Commented by mr W last updated on 20/Feb/21
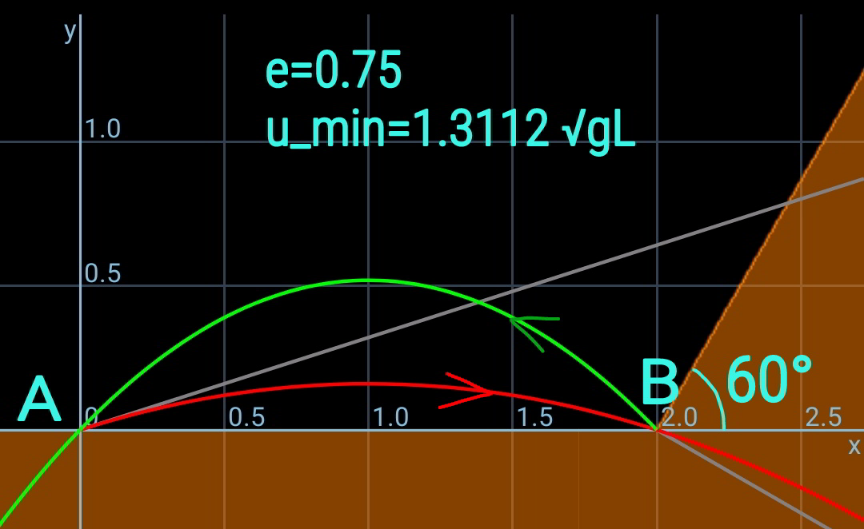
Commented by mr W last updated on 20/Feb/21
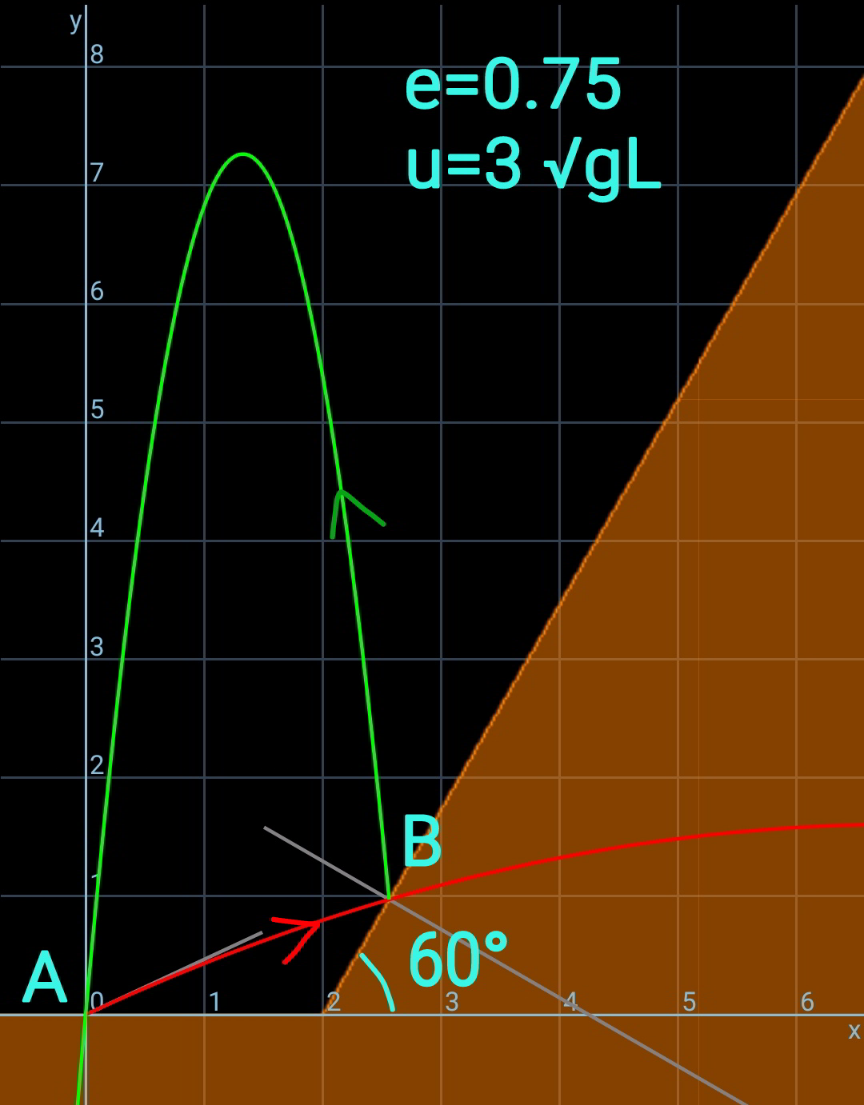
Commented by otchereabdullai@gmail.com last updated on 23/Feb/21

$$\mathrm{world}\:\mathrm{best}\:! \\ $$
