
Question and Answers Forum
Question Number 133191 by pticantor last updated on 19/Feb/21
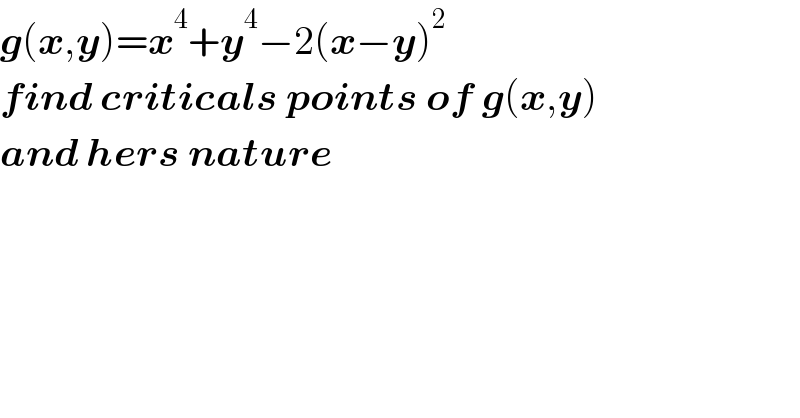
Answered by Olaf last updated on 20/Feb/21
![g(x,y) = x^4 +y^4 −2(x−y)^2 ▽g = [((∂g/∂x)),((∂g/∂y)) ] = [((4x^3 −2(x−y))),((4y^3 +2(x−y))) ] ▽g = [(0),(0) ]⇔ (x−y) = 2x^3 = −2y^3 ⇔ (x,y) = (0,0) : this is the only critical point. Hessian matrix : [((∂^2 g/∂x^2 ),(∂^2 g/(∂x∂y))),((∂^2 g/(∂y∂x)),(∂^2 g/∂y^2 )) ] = [((12x^2 −2x),2),(2,(12y^2 −2y)) ] Hessian matrix in (0,0) : Hess(g)∣_((0,0)) = [(0,2),(2,0) ] det(Hess(g)∣_((0,0)) ) = determinant ((0,2),(2,0))= −4 det(Hess(g)∣_((0,0)) ) < 0 ⇒ (0,0) is a saddle point](Q133207.png)
| ||
Question and Answers Forum | ||
Question Number 133191 by pticantor last updated on 19/Feb/21 | ||
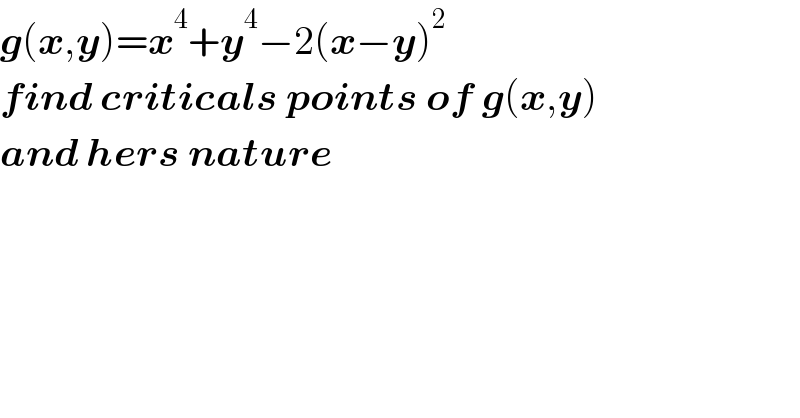 | ||
Answered by Olaf last updated on 20/Feb/21 | ||
![g(x,y) = x^4 +y^4 −2(x−y)^2 ▽g = [((∂g/∂x)),((∂g/∂y)) ] = [((4x^3 −2(x−y))),((4y^3 +2(x−y))) ] ▽g = [(0),(0) ]⇔ (x−y) = 2x^3 = −2y^3 ⇔ (x,y) = (0,0) : this is the only critical point. Hessian matrix : [((∂^2 g/∂x^2 ),(∂^2 g/(∂x∂y))),((∂^2 g/(∂y∂x)),(∂^2 g/∂y^2 )) ] = [((12x^2 −2x),2),(2,(12y^2 −2y)) ] Hessian matrix in (0,0) : Hess(g)∣_((0,0)) = [(0,2),(2,0) ] det(Hess(g)∣_((0,0)) ) = determinant ((0,2),(2,0))= −4 det(Hess(g)∣_((0,0)) ) < 0 ⇒ (0,0) is a saddle point](Q133207.png) | ||
| ||