
Question and Answers Forum
Question Number 133452 by bagjagunawan last updated on 22/Feb/21

Answered by mnjuly1970 last updated on 22/Feb/21
![𝛗=^(x=2y−1) ∫_((1/2) ) ^( 1) ((ln(2−2y)ln(ln(2y)))/(2y))(2)dy =∫_(1/2) ^( 1) (ln(2)+ln(1−y))(ln(2)+ln(y))(dy/y) =∫_(1/2) ^( 1) ((ln^2 (2)+ln(y).ln(2)+ln(2).ln(1−y)+ln(1−y).ln(y))/y) dy =[ln(y)ln(2)]_(1/2) ^1 +(1/2)[ln(2).ln^2 y]_(1/2) ^1 +ln(2)[li_((2)) ((1/2))−li_2 (1)]+∫_(1/2) ^( 1) ((ln(y)ln(1−y))/y)dy =ln^2 (2)−(1/2)ln^3 (2)+ln(2)[(π^2 /(12))−(1/2)ln^2 (2)−(π^2 /6)]−Φ....(∗) Φ=[−li_2 (y).ln(y)]_(1/2) ^1 +∫_((1/2) ) ^( 1) ((li_2 (y))/y)dy =−li_2 ((1/2))+li_3 (1)−li_3 ((1/2)) =((−π^2 )/(12))+(1/2)ln^2 (2)+ζ(3)−[(7/8)ζ(3)+(1/6)ln^3 (2)−(π^2 /(12))ln(2)] =(1/8)ζ(3)+(1/2)ln^2 (2)+(1/6)ln^3 (2)−(π^2 /(12)) +(π^2 /(12))ln(2) (∗∗) replacing (∗) → (∗∗)](Q133456.png)
Commented by bagjagunawan last updated on 22/Feb/21
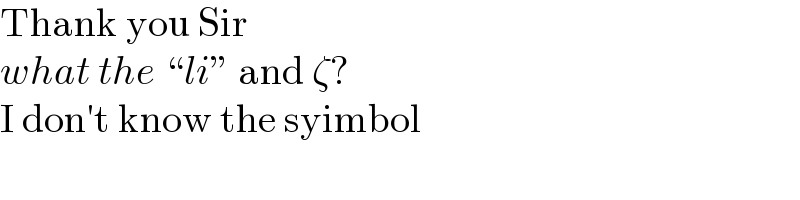
Commented by mnjuly1970 last updated on 22/Feb/21

| ||
Question and Answers Forum | ||
Question Number 133452 by bagjagunawan last updated on 22/Feb/21 | ||
 | ||
Answered by mnjuly1970 last updated on 22/Feb/21 | ||
![𝛗=^(x=2y−1) ∫_((1/2) ) ^( 1) ((ln(2−2y)ln(ln(2y)))/(2y))(2)dy =∫_(1/2) ^( 1) (ln(2)+ln(1−y))(ln(2)+ln(y))(dy/y) =∫_(1/2) ^( 1) ((ln^2 (2)+ln(y).ln(2)+ln(2).ln(1−y)+ln(1−y).ln(y))/y) dy =[ln(y)ln(2)]_(1/2) ^1 +(1/2)[ln(2).ln^2 y]_(1/2) ^1 +ln(2)[li_((2)) ((1/2))−li_2 (1)]+∫_(1/2) ^( 1) ((ln(y)ln(1−y))/y)dy =ln^2 (2)−(1/2)ln^3 (2)+ln(2)[(π^2 /(12))−(1/2)ln^2 (2)−(π^2 /6)]−Φ....(∗) Φ=[−li_2 (y).ln(y)]_(1/2) ^1 +∫_((1/2) ) ^( 1) ((li_2 (y))/y)dy =−li_2 ((1/2))+li_3 (1)−li_3 ((1/2)) =((−π^2 )/(12))+(1/2)ln^2 (2)+ζ(3)−[(7/8)ζ(3)+(1/6)ln^3 (2)−(π^2 /(12))ln(2)] =(1/8)ζ(3)+(1/2)ln^2 (2)+(1/6)ln^3 (2)−(π^2 /(12)) +(π^2 /(12))ln(2) (∗∗) replacing (∗) → (∗∗)](Q133456.png) | ||
| ||
Commented by bagjagunawan last updated on 22/Feb/21 | ||
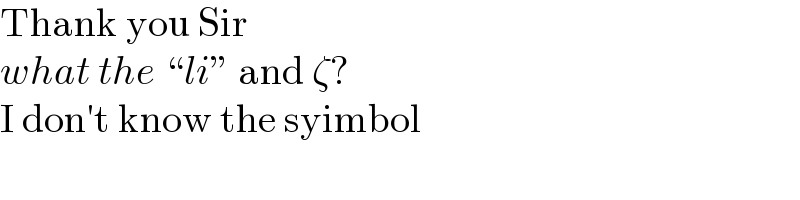 | ||
Commented by mnjuly1970 last updated on 22/Feb/21 | ||
 | ||