Question Number 13364 by tawa tawa last updated on 19/May/17
$$\int_{\:\:\:\mathrm{0}} ^{\:\:\frac{\mathrm{3}\sqrt{\mathrm{3}}}{\mathrm{2}}} \:\:\:\frac{\mathrm{x}^{\mathrm{3}} }{\sqrt{\mathrm{4x}^{\mathrm{2}} \:−\:\mathrm{9}}}\:\:\mathrm{dx} \\ $$
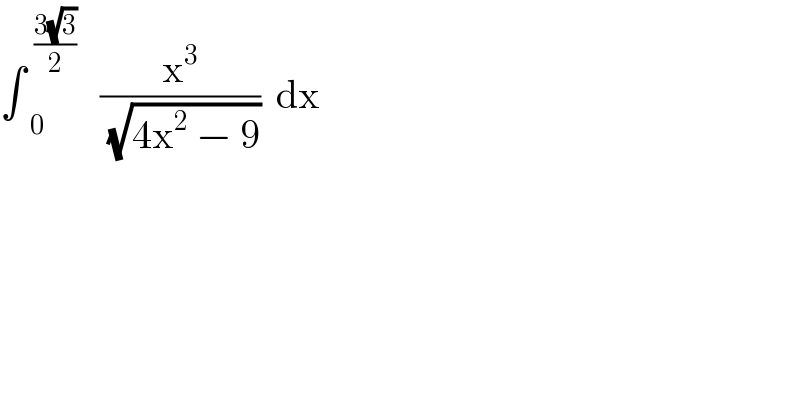
Commented by b.e.h.i.8.3.4.1.7@gmail.com last updated on 19/May/17
![you should change the limits of integral. function have not real valves in interval:[0,((3(√3))/2)].](Q13393.png)
$${you}\:{should}\:{change}\:{the}\:{limits}\:{of}\:{integral}. \\ $$$${function}\:{have}\:{not}\:{real}\:{valves}\:{in}\:{interval}:\left[\mathrm{0},\frac{\mathrm{3}\sqrt{\mathrm{3}}}{\mathrm{2}}\right]. \\ $$
Answered by ajfour last updated on 19/May/17
$${considering}\:\:\:{I}=\int\frac{{x}^{\mathrm{3}} }{\sqrt{\mathrm{4}{x}^{\mathrm{2}} −\mathrm{9}}}\:{dx} \\ $$$${let}\:\boldsymbol{{t}}=\mathrm{4}{x}^{\mathrm{2}} −\mathrm{9} \\ $$$${dt}=\mathrm{8}{xdx} \\ $$$${tdt}=\mathrm{32}{x}^{\mathrm{3}} {dx}−\mathrm{9}×\mathrm{8}{xdx} \\ $$$$\:\:\:\:\:\mathrm{32}{x}^{\mathrm{3}} {dx}\:=\left({t}+\mathrm{9}\right){dt} \\ $$$${so},\:\: \\ $$$${I}=\frac{\mathrm{1}}{\mathrm{32}}\int\:\frac{\left({t}+\mathrm{9}\right){dt}}{\sqrt{{t}}} \\ $$$$\:=\frac{\mathrm{1}}{\mathrm{32}}\left(\frac{\mathrm{3}}{\mathrm{2}}{t}^{\mathrm{3}/\mathrm{2}} +\mathrm{18}\sqrt{{t}}\right)+{C} \\ $$$$\:=\frac{\mathrm{3}}{\mathrm{64}}\left(\mathrm{4}{x}^{\mathrm{2}} −\mathrm{9}\right)^{\mathrm{3}/\mathrm{2}} +\frac{\mathrm{9}}{\mathrm{16}}\left(\mathrm{4}{x}^{\mathrm{2}} −\mathrm{9}\right)+{C} \\ $$$${if}\:{the}\:{limits}\:{were}\:{appropriate} \\ $$$${i}\:{would}\:{have}\:{tried}\:{to}\:{get}\:{an}\:{answer}. \\ $$
Commented by tawa tawa last updated on 19/May/17
$$\mathrm{God}\:\mathrm{bless}\:\mathrm{you}\:\mathrm{sir} \\ $$
Answered by b.e.h.i.8.3.4.1.7@gmail.com last updated on 19/May/17
![((2x)/3)=i.tgt⇒dx=(3/2)i(1+tg^2 t)dt⇒ cost=(1/(√(1−((4x^2 )/9))))=(3/(√(9−4x^2 )))=((−3i)/(√(4x^2 −9))) 4x^2 −9=−4.(9/4)tg^2 t−9=−9(tg^2 t+1)= =((−9)/(cos^2 t)) (i^2 =−1) I=∫((((27)/8)i^3 .tg^3 t.(3/2)i.(1+tg^2 t)dt)/(3i/cost))= =−((27)/(16))i∫((cost.tg^3 t)/(cos^2 t))dt=−((27i)/(16))∫((sin^3 t)/(cos^4 t))dt= =−((27i)/(16))∫((sint(1−cos^2 t)dt)/(cos^4 t))= =((−27i)/(16))∫[((sint)/(cos^4 t))−((sint)/(cos^2 t))]dt= =((−27i)/(16))(−(1/(5cos^5 t))+(1/(cos^3 t)))+C.= =((−27i)/(16))(−(1/5)(((4x^2 −9)^2 (√(4x^2 −9)))/(−3^5 i))+(((4x^2 −9)(√(4x^2 −9)))/(−27i)))+C= =((−(4x^2 −9)(√(4x^2 −9)))/(16×45))(4x^2 −54)+C=F(x) F(((3(√3))/2))=((−18(√(18)))/(16×45))(27−54)=+((81)/(40))(√2) F(0)=((27i)/(16×45))(−54)=−((81)/(40))i ⇒I=((81)/(40))((√2)−i) .■](Q13386.png)
$$\frac{\mathrm{2}{x}}{\mathrm{3}}={i}.{tgt}\Rightarrow{dx}=\frac{\mathrm{3}}{\mathrm{2}}{i}\left(\mathrm{1}+{tg}^{\mathrm{2}} {t}\right){dt}\Rightarrow \\ $$$${cost}=\frac{\mathrm{1}}{\sqrt{\mathrm{1}−\frac{\mathrm{4}{x}^{\mathrm{2}} }{\mathrm{9}}}}=\frac{\mathrm{3}}{\sqrt{\mathrm{9}−\mathrm{4}{x}^{\mathrm{2}} }}=\frac{−\mathrm{3}{i}}{\sqrt{\mathrm{4}{x}^{\mathrm{2}} −\mathrm{9}}} \\ $$$$\mathrm{4}{x}^{\mathrm{2}} −\mathrm{9}=−\mathrm{4}.\frac{\mathrm{9}}{\mathrm{4}}{tg}^{\mathrm{2}} {t}−\mathrm{9}=−\mathrm{9}\left({tg}^{\mathrm{2}} {t}+\mathrm{1}\right)= \\ $$$$=\frac{−\mathrm{9}}{{cos}^{\mathrm{2}} {t}}\:\:\:\:\:\:\left(\boldsymbol{{i}}^{\mathrm{2}} =−\mathrm{1}\right) \\ $$$${I}=\int\frac{\frac{\mathrm{27}}{\mathrm{8}}\boldsymbol{{i}}^{\mathrm{3}} .{tg}^{\mathrm{3}} {t}.\frac{\mathrm{3}}{\mathrm{2}}\boldsymbol{{i}}.\left(\mathrm{1}+{tg}^{\mathrm{2}} {t}\right){dt}}{\mathrm{3}\boldsymbol{{i}}/\boldsymbol{{cost}}}= \\ $$$$=−\frac{\mathrm{27}}{\mathrm{16}}\boldsymbol{{i}}\int\frac{\boldsymbol{{cost}}.\boldsymbol{{tg}}^{\mathrm{3}} \boldsymbol{{t}}}{\boldsymbol{{cos}}^{\mathrm{2}} \boldsymbol{{t}}}\boldsymbol{{dt}}=−\frac{\mathrm{27}\boldsymbol{{i}}}{\mathrm{16}}\int\frac{{sin}^{\mathrm{3}} {t}}{{cos}^{\mathrm{4}} {t}}{dt}= \\ $$$$=−\frac{\mathrm{27}\boldsymbol{{i}}}{\mathrm{16}}\int\frac{{sint}\left(\mathrm{1}−{cos}^{\mathrm{2}} {t}\right){dt}}{{cos}^{\mathrm{4}} {t}}= \\ $$$$=\frac{−\mathrm{27}\boldsymbol{{i}}}{\mathrm{16}}\int\left[\frac{{sint}}{{cos}^{\mathrm{4}} {t}}−\frac{{sint}}{{cos}^{\mathrm{2}} {t}}\right]{dt}= \\ $$$$=\frac{−\mathrm{27}\boldsymbol{{i}}}{\mathrm{16}}\left(−\frac{\mathrm{1}}{\mathrm{5}\boldsymbol{{cos}}^{\mathrm{5}} \boldsymbol{{t}}}+\frac{\mathrm{1}}{\boldsymbol{{cos}}^{\mathrm{3}} \boldsymbol{{t}}}\right)+\boldsymbol{{C}}.= \\ $$$$=\frac{−\mathrm{27}\boldsymbol{{i}}}{\mathrm{16}}\left(−\frac{\mathrm{1}}{\mathrm{5}}\frac{\left(\mathrm{4}\boldsymbol{{x}}^{\mathrm{2}} −\mathrm{9}\right)^{\mathrm{2}} \sqrt{\mathrm{4}\boldsymbol{{x}}^{\mathrm{2}} −\mathrm{9}}}{−\mathrm{3}^{\mathrm{5}} \boldsymbol{{i}}}+\frac{\left(\mathrm{4}\boldsymbol{{x}}^{\mathrm{2}} −\mathrm{9}\right)\sqrt{\mathrm{4}\boldsymbol{{x}}^{\mathrm{2}} −\mathrm{9}}}{−\mathrm{27}\boldsymbol{{i}}}\right)+\boldsymbol{{C}}= \\ $$$$=\frac{−\left(\mathrm{4}{x}^{\mathrm{2}} −\mathrm{9}\right)\sqrt{\mathrm{4}{x}^{\mathrm{2}} −\mathrm{9}}}{\mathrm{16}×\mathrm{45}}\left(\mathrm{4}{x}^{\mathrm{2}} −\mathrm{54}\right)+\boldsymbol{{C}}=\boldsymbol{{F}}\left({x}\right) \\ $$$${F}\left(\frac{\mathrm{3}\sqrt{\mathrm{3}}}{\mathrm{2}}\right)=\frac{−\mathrm{18}\sqrt{\mathrm{18}}}{\mathrm{16}×\mathrm{45}}\left(\mathrm{27}−\mathrm{54}\right)=+\frac{\mathrm{81}}{\mathrm{40}}\sqrt{\mathrm{2}} \\ $$$${F}\left(\mathrm{0}\right)=\frac{\mathrm{27}\boldsymbol{{i}}}{\mathrm{16}×\mathrm{45}}\left(−\mathrm{54}\right)=−\frac{\mathrm{81}}{\mathrm{40}}\boldsymbol{{i}} \\ $$$$\Rightarrow\boldsymbol{{I}}=\frac{\mathrm{81}}{\mathrm{40}}\left(\sqrt{\mathrm{2}}−\boldsymbol{{i}}\right)\:\:\:\:.\blacksquare \\ $$