((sin1)/e)−((sin(2))/(2e^2 ))+((sin(3))/(3e^3 ))−((sin(4))/(4e^4 ))+...=tan^(−1) (((sin(1))/(cos(1)+e)))


Question and Answers Forum

All Questions Topic List
Others Questions
Previous in All Question Next in All Question
Previous in Others Next in Others
Question Number 133692 by Dwaipayan Shikari last updated on 23/Feb/21

$\frac{s i n 1}{e} - \frac{s i n (2)}{2 e^{2}} + \frac{s i n (3)}{3 e^{3}} - \frac{s i n (4)}{4 e^{4}} + . . . = {t a n}^{- 1} (\frac{s i n (1)}{c o s (1) + e})$
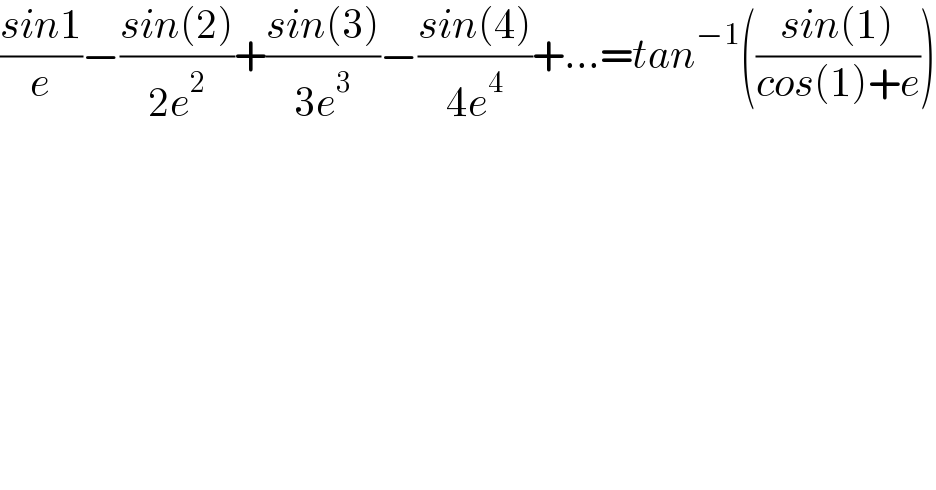
Commented by Dwaipayan Shikari last updated on 23/Feb/21

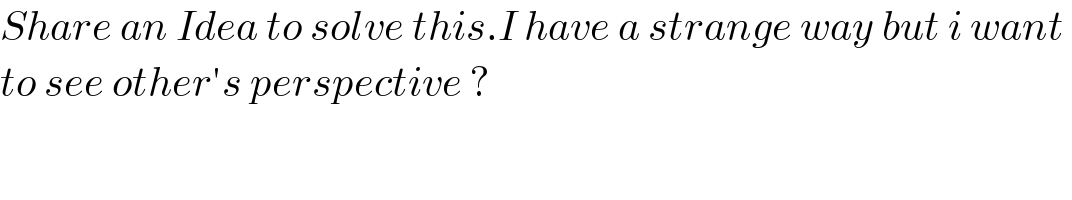
$S h a r e a n I d e a t o s o l v e t h i s . I h a v e a s t r a n g e w a y b u t i w a n t$ $t o s e e {o t h e r}^{'} s p e r s p e c t i v e ?$
	Answered by mindispower last updated on 23/Feb/21

	$= \frac{s i n (k)}{{n e}^{k}} = I m \sum_{m ⩾ 1} {(- 1)}^{m} \frac{e^{i m}}{{m e}^{m}}$ $= I m - l n (1 + e^{(i - 1)})$ $= - a r g (1 + e^{i} . e^{- 1}) = - {t g}^{-} (\frac{e^{- 1} s i n (1)}{1 + e^{- 1} c o s (1)})$ $= - {t g}^{-} (\frac{s i n (1)}{e + c o s (1)}) = \frac{π}{2} - {t g}^{-} (\frac{e + c o s (1)}{s i n (1)})$
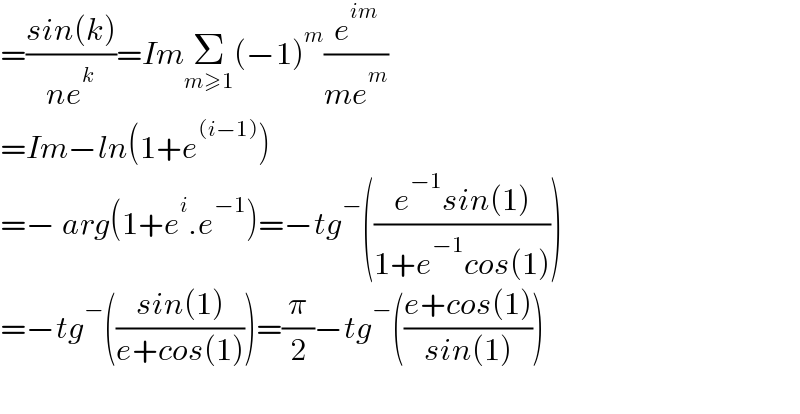
	Commented by Dwaipayan Shikari last updated on 23/Feb/21

	$S i r f i r s t l i n e \underset{m ⩾ 1}{\sum^{\infty}} \frac{{(- 1)}^{m + 1}}{m e} e^{i m}$
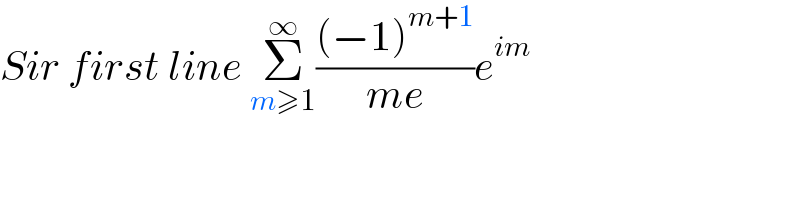
	Commented by mindispower last updated on 23/Feb/21

	$t h a n x y e s s i r s o r r y t o o b u s y t h i s d a y s$ $b a c k s o o n$
	Answered by Dwaipayan Shikari last updated on 23/Feb/21

	$l o g (1 + {a e}^{i θ}) = l o g (\sqrt{2 + 2 a c o s θ}) + {i t a n}^{- 1} \frac{a s i n θ}{a c o s θ + 1}$ ${a e}^{i θ} - \frac{a^{2} e^{2 i θ}}{2} + \frac{a^{3} e^{3 i θ}}{3} - . . . = l o g (\sqrt{2 + 2 a c o s θ}) + {i t a n}^{- 1} \frac{a s i n θ}{a c o s θ + 1}$ $a c o s θ - \frac{a^{2}}{2} c o s 2 θ + \frac{a^{3}}{3} c o s 3 θ - . . . = l o g (\sqrt{2 + 2 a c o s θ})$ $a s i n θ - \frac{a^{2}}{2} s i n 2 θ + \frac{a^{3}}{3} s i n 3 θ - . . . = {t a n}^{- 1} \frac{a s i n θ}{a c o s θ + 1}$ $a = \frac{1}{e}$
Terms of Service
Privacy Policy
Contact: info@tinkutara.com

Question and Answers Forum