Question and Answers Forum

All Questions      Topic List

None Questions

Previous in All Question      Next in All Question      

Previous in None      Next in None      

Question Number 133856 by mathocean1 last updated on 24/Feb/21

$$$$$$\{\begin{array}{l}{U}_0=1\\ U_1=2\\ U_{n+2}=\frac{3}{2}{U}_{n+1}-\frac{1}{2}{U}_n\end{array}$$$$Determinatethesmallestinteger$$$$n_{0}suchthat\mathrm{\forall }n⩾n_{0}wehave\mid U_n-3\mid ⩽{10}^{-4}$$

Answered by mr W last updated on 25/Feb/21

$$x^2-\frac{3}{2}x+\frac{1}{2}=0$$$$(x-1)(x-\frac{1}{2})=0$$$$x=1,\frac{1}{2}$$$$\Rightarrow U_n=A+\frac{B}{2^n}$$$$U_0=A+B=1$$$$U_1=A+\frac{B}{2}=2$$$$\Rightarrow B=-2,A=3$$$$\Rightarrow U_n=3-\frac{1}{2^{n-1}}$$$$\underset{n\to \mathrm{\infty }}{\lim }{U}_n=3$$$$\mid U_n-3\mid =\frac{1}{2^{n-1}}⩽{10}^{-4}$$$$2^{n-1}⩾{10}^4$$$$n⩾1+{\log }_2{10}^4=1+\frac{4}{\log 2}\approx 14.29$$$$\Rightarrow n_0=15$$

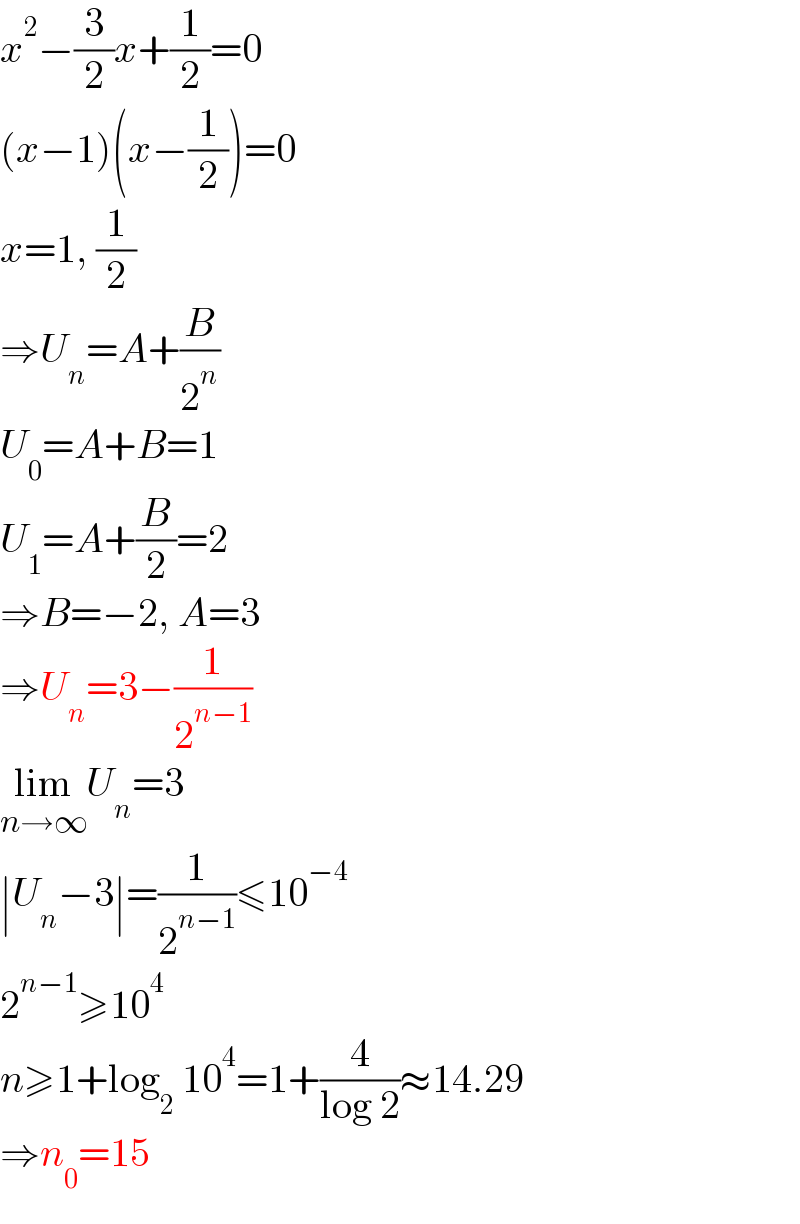
Commented by mathocean1 last updated on 27/Feb/21

$$wow{it}^{\prime }sgreatsir...$$$$Canyouexplainmehowyoufindthe$$$$firstandfourthlinesplease...$$

Commented by mr W last updated on 27/Feb/21

$$wecanuse‘‘characteristicroot{method}^{″}$$$$tosolvethiskindofproblemswith$$$$‘‘recurrence{relation}^{″}.youmayget$$$$someexplanationhere:$$$$(justreadthetextafterexample2.4.5.$$

Commented by mr W last updated on 27/Feb/21

Commented by mr W last updated on 27/Feb/21

https://math.libretexts.org/Courses/Saint_Mary's_College_Notre_Dame_IN/SMC%3A_MATH_339_-_Discrete_Mathematics_(Rohatgi)/Text/2%3A_Sequences/2.4%3A_Solving_Recurrence_Relations

Commented by mathocean1 last updated on 27/Feb/21

$$Super!$$$$$$$$Thankyouverymuchsir...$$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com