
Question and Answers Forum
Question Number 13394 by Tinkutara last updated on 19/May/17
![Show that any circle with centre ((√2), (√3)) cannot pass through more than one lattice point. [Lattice points are points in cartesian plane, whose abscissa and ordinate both are integers.]](Q13394.png)
Answered by mrW1 last updated on 20/May/17
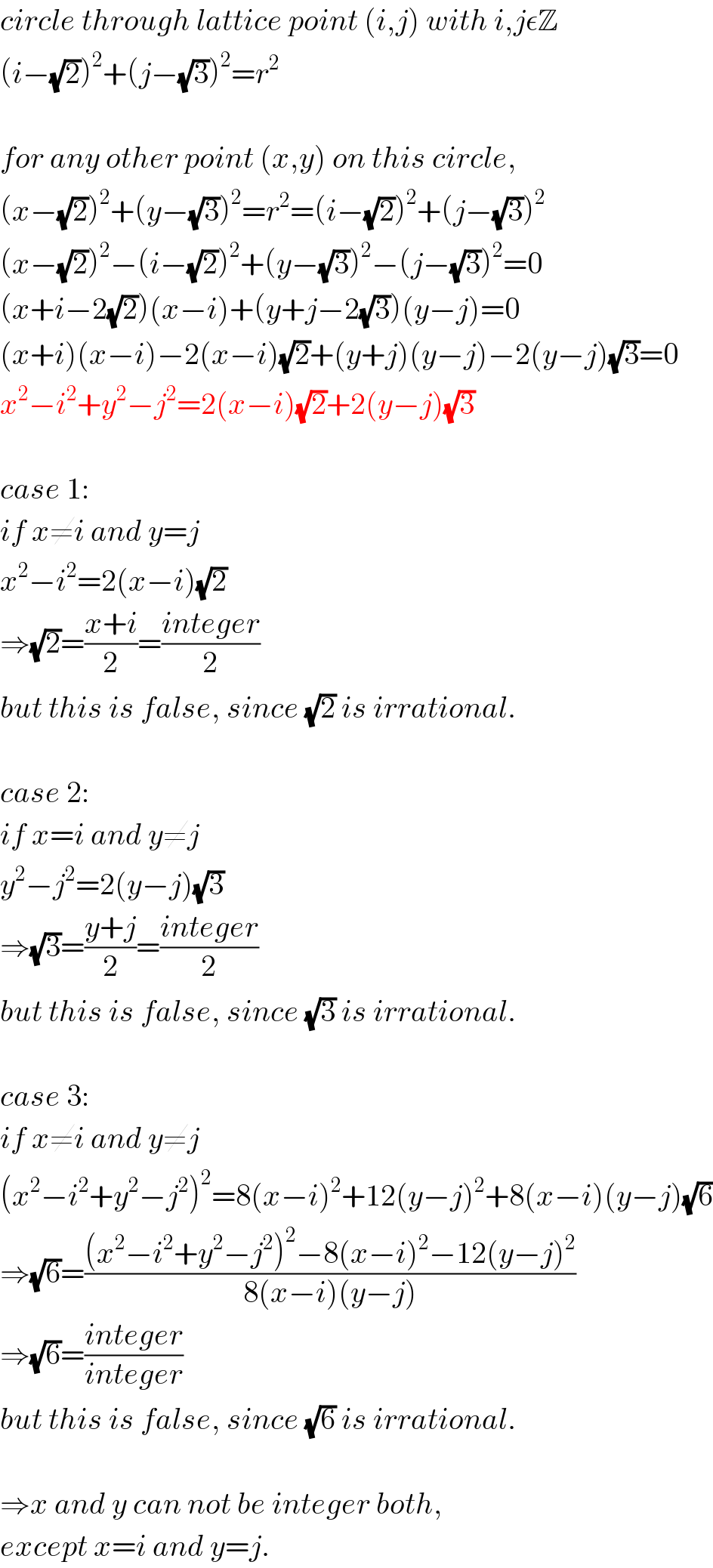
| ||
Question and Answers Forum | ||
Question Number 13394 by Tinkutara last updated on 19/May/17 | ||
![Show that any circle with centre ((√2), (√3)) cannot pass through more than one lattice point. [Lattice points are points in cartesian plane, whose abscissa and ordinate both are integers.]](Q13394.png) | ||
Answered by mrW1 last updated on 20/May/17 | ||
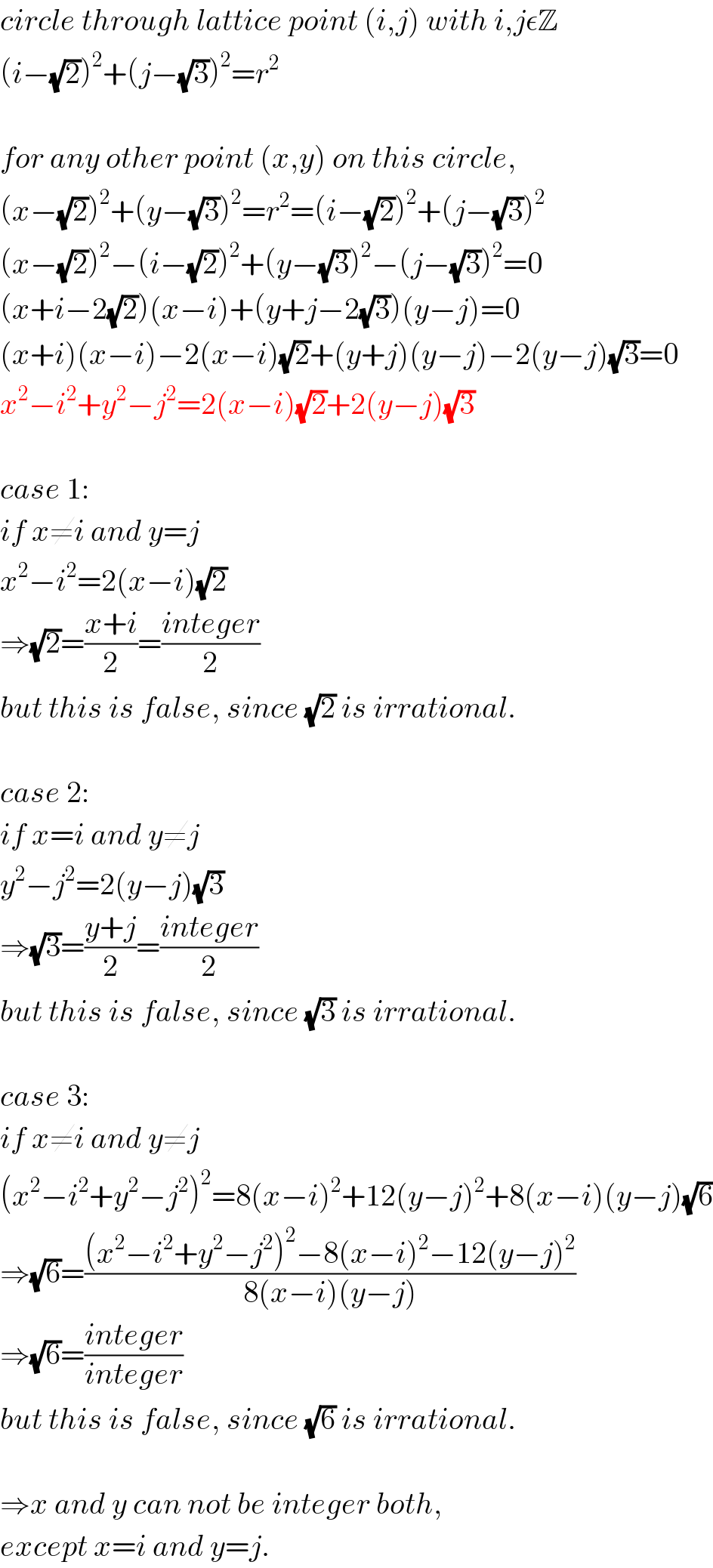 | ||
| ||