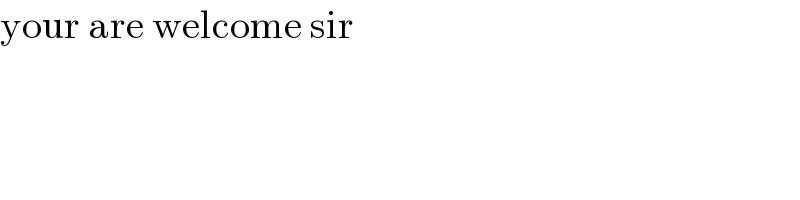.....mathematical analysis..... prove that:: 1: 𝛗=∫_0 ^( 1) ln(Γ(x))cos^2 (πx)dx=((ln(2π))/4)+(π/8) ..✓ 2: lim_(n→∞) ((Γ(n+1)Γ(n+2))/(Γ^2 (n+(3/2)))) =1...✓


Question and Answers Forum

All Questions Topic List
Limits Questions
Previous in All Question Next in All Question
Previous in Limits Next in Limits
Question Number 134079 by mnjuly1970 last updated on 27/Feb/21

$. . . . . m a t h e m a t i c a l a n a l y s i s . . . . .$ $p r o v e t h a t ::$ $1 : ϕ = \int_{0}^{1} l n (Γ (x)) {c o s}^{2} (π x) d x = \frac{l n (2 π)}{4} + \frac{π}{8} . . ✓$ $2 : {l i m}_{n \to \infty} \frac{Γ (n + 1) Γ (n + 2)}{Γ^{2} (n + \frac{3}{2})} = 1 . . . ✓$
	Answered by mathmax by abdo last updated on 27/Feb/21

	$Φ = \int_{0}^{1} \ln (Γ (x) \cos^{2} (π x) dx changement x = 1 - t give$ $Φ = \int_{0}^{1} \ln (Γ (1 - x)) \cos^{2} (π x) dt we know Γ (x) . Γ (1 - x) = \frac{π}{\sin (π x)}$ $\Rightarrow \ln (Γ (x)) + \ln (Γ (1 - x)) = \ln (π) - \ln (\sin (π x)) \Rightarrow$ $\int_{0}^{1} \ln (Γ (x)) \cos^{2} (π x) dx + \int_{0}^{1} \ln (Γ (1 - x)) \cos^{2} (π x) dx$ $= \ln (π) \int_{0}^{1} \cos^{2} (π x) dx - \int_{0}^{1} \ln (\sin (π x) \cos^{2} (π x) dx \Rightarrow$ $2 Φ = \frac{\ln (π)}{2} \int_{0}^{1} (1 + \cos (2 π x)) dx - \frac{1}{2} \int_{0}^{1} (1 + \cos (2 π x)) \ln (\sin π x) dx$ $we have \int_{0}^{1} (1 + \cos (2 π x) dx = 1 + {[\frac{1}{2 π} \sin (2 π x)]}_{0}^{1} = 1$ $\int_{0}^{1} (1 + \cos (2 π x)) \ln (\sin (π x)) dx = \int_{0}^{1} \ln (\sin (π x)) dx$ $+ \int_{0}^{1} \cos (2 π x) \ln (\sin (π x) dx and \int_{0}^{1} \ln (\sin (π x)) dx =_{π x = t} \int_{0}^{π} \ln (sint) \frac{dt}{π}$ $= \frac{1}{π} (\int_{0}^{\frac{π}{2}} \ln (sint) dt + \int_{\frac{π}{2}}^{π} \ln (sint) dt (\to t = \frac{π}{2} + u)$ $= \frac{1}{π} (- \frac{π}{2} \ln (2) - \frac{π}{2} \ln (2)) = - \ln (2)$ $\int_{0}^{1} \cos (2 π x) \ln (\sin (π x) dx = [\frac{1}{2 π} \sin (2 π x) \ln {(\sin (π x)]}_{0}^{1}$ $- \int_{0}^{1} \frac{1}{2 π} \sin (2 π x) \frac{π \cos (π x)}{\sin (π x)} dx$ $= - \frac{1}{2} \int_{0}^{1} 2 \sin (π x) \cos (π x) \frac{\cos (π x)}{\sin (π x)} dx$ $= - \int_{0}^{1} \cos^{2} (π x) dx = - \frac{1}{2} \int_{0}^{1} (1 + \cos (2 π x)) dx = - \frac{1}{2} \Rightarrow$ $2 Φ = \frac{\ln (π)}{2} - \frac{1}{2} (- \ln 2 - \frac{1}{2}) = \frac{\ln (π)}{2} + \frac{\ln (2)}{2} + \frac{1}{4} \Rightarrow$ $Φ = \frac{\ln (π)}{4} + \frac{\ln (2)}{4} + \frac{1}{8} \Rightarrow Φ = \frac{\ln (2 π)}{4} + \frac{1}{8}$
	Commented by mnjuly1970 last updated on 27/Feb/21

	$t h a n k y o u s i r$
	Answered by mathmax by abdo last updated on 28/Feb/21

	$Γ (n + 1) = n! \sim n^{n} e^{- n} \sqrt{2 π n}$ $Γ (n + 2) = (n + 1)! \sim {(n + 1)}^{n + 1} e^{- (n + 1)} \sqrt{2 π (n + 1)}$ $Γ (n + \frac{3}{2}) = (n + \frac{1}{2})! \sim {(n + \frac{1}{2})}^{n + \frac{1}{2}} e^{- (n + \frac{1}{2})} \sqrt{2 π (n + \frac{1}{2})} \Rightarrow$ $Γ^{2} (n + \frac{3}{2}) = {(n + \frac{1}{2})}^{2 n + 1} e^{- (2 n + 1)} (2 π (n + \frac{1}{2})) \Rightarrow$ $V_{n} \sim \frac{n^{n} e^{- n} \sqrt{2 π n} . {(n + 1)}^{n + 1} e^{- (n + 1)} \sqrt{2 π (n + 1})}{{(n + \frac{1}{2})}^{2 n + 1} e^{- (2 n + 1)} π (2 n + 1)}$ $= \frac{n^{2 n + 1} e^{- (2 n + 1)} {(1 + \frac{1}{n})}^{n + 1} 2 π \sqrt{n^{2} + n}}{{(n + \frac{1}{2})}^{2 n + 1} e^{- (2 n + 1)} π (2 n + 1)}$ $= {(\frac{n}{n + \frac{1}{2}})}^{2 n + 1} {(1 + \frac{1}{n})}^{n + 1} \Rightarrow$ $V_{n} \sim e^{(2 n + 1) \ln (\frac{n}{n + \frac{1}{2}})} . e^{(n + 1) \ln (1 + \frac{1}{n})} we have$ $\ln (\frac{n}{n + \frac{1}{2}}) = \ln (1 - \frac{1}{2 (n + \frac{1}{2})}) = \ln (1 - \frac{1}{2 n + 1}) \sim - \frac{1}{2 n + 1}$ $\Rightarrow (2 n + 1) \ln (. . .) \sim e^{- 1} also (n + 1) \ln (1 + \frac{1}{n}) \sim \frac{n + 1}{n} \sim 1 \Rightarrow$ $e^{(n + 1) \ln (. . .)} \sim e \Rightarrow \lim_{n \to + \infty} V_{n} = e^{- 1} . e = 1$
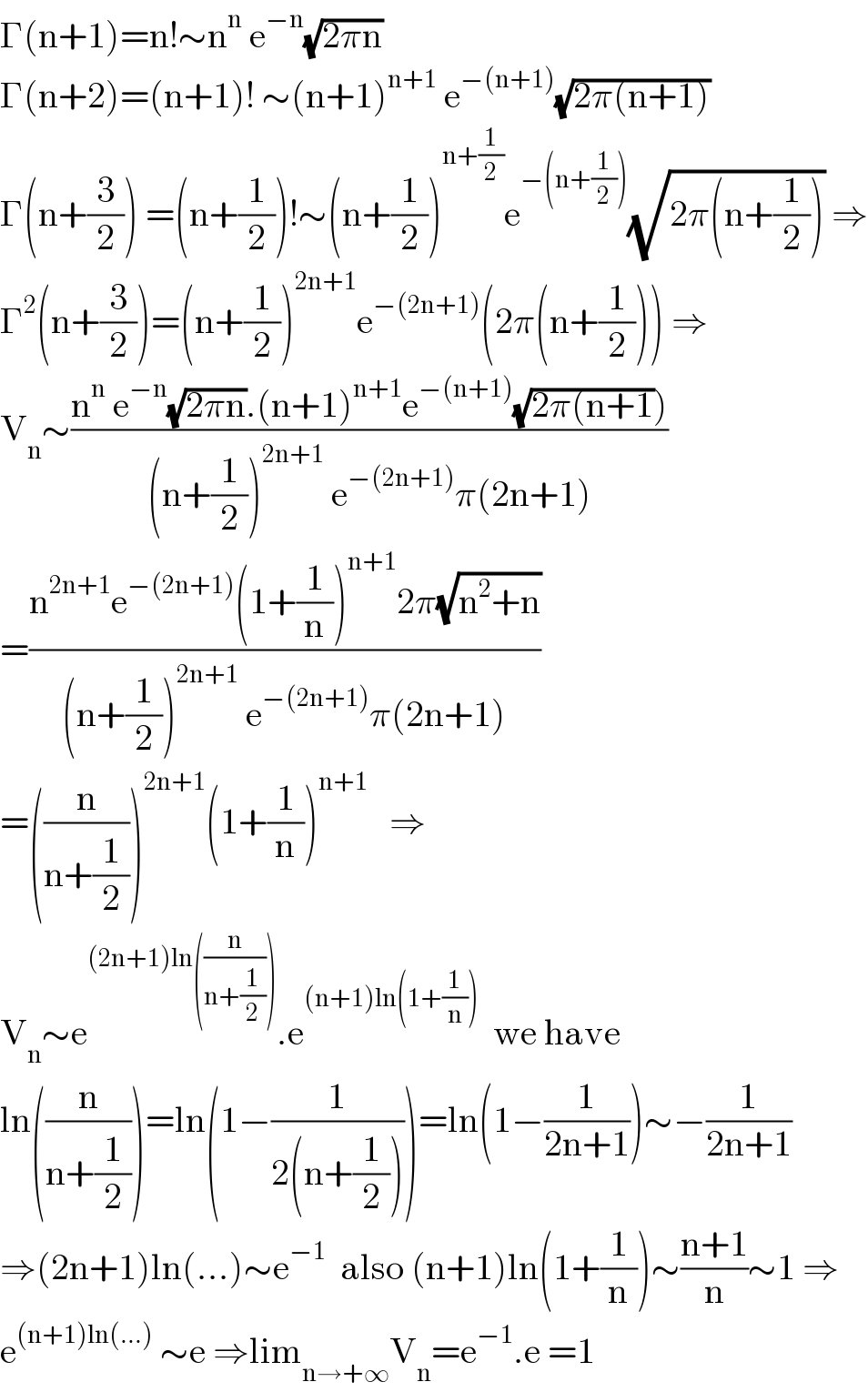
	Commented by mnjuly1970 last updated on 28/Feb/21

	$t h a n k s a l o t s i r m a t h m x a x$ $e x c e l l e n t . . . t a y e b a l l a h . . .$
	Commented by mathmax by abdo last updated on 06/Mar/21

	$your are welcome sir$
Terms of Service
Privacy Policy
Contact: info@tinkutara.com

Question and Answers Forum