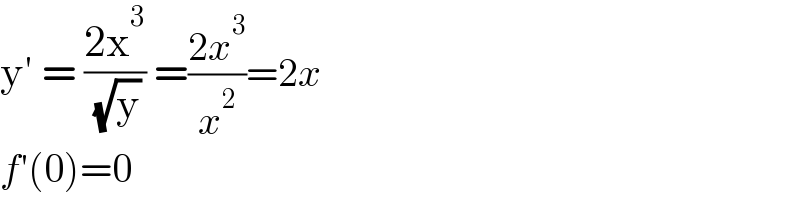Question and Answers Forum

All Questions      Topic List

Differentiation Questions

Previous in All Question      Next in All Question      

Previous in Differentiation      Next in Differentiation      

Question Number 134127 by bobhans last updated on 28/Feb/21

$$\mathrm{Given}\mid \mathrm{f}\left(\mathrm{x}\right)\mid ={\mathrm{x}}^2\mathrm{for}-1<\mathrm{x}<1$$ $$\mathrm{find}\mathrm{f}{}^{\prime }\left(0\right).$$

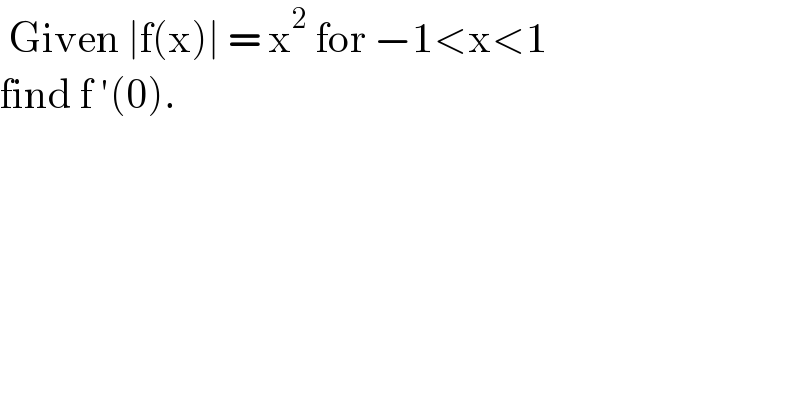
Commented byEDWIN88 last updated on 28/Feb/21

$$\mathrm{does}\mathrm{not}\mathrm{exist}$$

Commented byEDWIN88 last updated on 28/Feb/21

Commented byMJS_new last updated on 28/Feb/21

$$\mathrm{proper}\mathrm{maths}:$$ $${\mathrm{let}}^{\prime }\mathrm{s}\mathrm{try}\mathrm{with}$$ $$f\left(x\right)=2x\mathrm{\forall }x\in \mathbb{R}$$ $$\mathrm{this}\mathrm{simply}\mathrm{means},{\mathrm{we}}^{\prime }\mathrm{re}\mathrm{assigning}x\to 2x$$ $$\mathrm{or}y=2x$$ $$\mid f\left(x\right)\mid =2x\mathrm{is}\mathrm{not}\mathrm{a}\mathrm{function}\mathrm{anymore}$$ $$\mid y\mid =2x\iff y=\pm 2x\wedge x⩾0$$ $$\mathrm{we}\mathrm{can}\mathrm{split}\mathrm{the}\mathrm{branches}:$$ $$y_1=-2x\wedge x⩾0$$ $$y_2=2x\wedge x⩾0$$ $$\frac{{dy}_1}{dx}\mathrm{and}\frac{{dy}_2}{dx}\mathrm{both}\mathrm{exist}\mathrm{but}\frac{dy}{dx}{\mathrm{doesn}}^{\prime }\mathrm{t}\mathrm{exist}$$ $$$$ $$\mathrm{now}$$ $$\mid f\left(x\right)\mid =x^2\mathrm{\forall }x\in \mathbb{R}$$ $$y=\pm x^2\wedge x^2⩾0\mathrm{but}{x}^2⩾0\mathrm{\forall }x\in \mathbb{R}$$ $$\mathrm{again}\mathrm{we}\mathrm{have}2\mathrm{branches}:$$ $$y_1=-x^2\mathrm{\forall }x\in \mathbb{R}$$ $$y_2=x^2\mathrm{\forall }x\in \mathbb{R}$$ $$\mathrm{again}\frac{{dy}_1}{dx}\mathrm{and}\frac{{dy}_2}{dx}\mathrm{exist}\mathrm{but}\frac{dy}{dx}{\mathrm{doesn}}^{\prime }\mathrm{t}\mathrm{exist}$$ $$\mathrm{anyway}\mathrm{for}x=0\mathrm{we}\mathrm{have}\frac{{dy}_1}{dx}=\frac{{dy}_2}{dx}=0$$ $$\mathrm{but}\mathrm{this}\mathrm{still}{\mathrm{doesn}}^{\prime }\mathrm{t}\mathrm{mean}\mathrm{that}\frac{dy}{dx}=0\mathrm{for}x=0$$

Answered by EDWIN88 last updated on 28/Feb/21

$$\mid \mathrm{y}\mid ={\mathrm{x}}^2\Rightarrow \sqrt{{\mathrm{y}}^2}={\mathrm{x}}^2;{\mathrm{y}}^2={\mathrm{x}}^4$$ $$2\mathrm{y}{\mathrm{y}}^{\prime }={4\mathrm{x}}^3,{\mathrm{y}}^{\prime }=\frac{{2\mathrm{x}}^3}{\sqrt{\mathrm{y}}}=\frac{0}{0}\left(\mathrm{does}\mathrm{not}\mathrm{exist}\right)$$

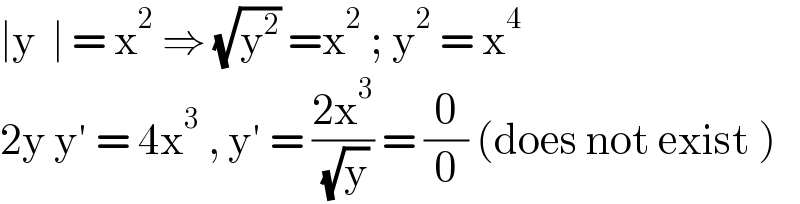
Commented bymr W last updated on 28/Feb/21

$${\mathrm{y}}^{\prime }=\frac{{2\mathrm{x}}^3}{\sqrt{\mathrm{y}}}=\frac{2x^3}{x^2}=2x$$ $$f^{\prime }\left(0\right)=0$$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com