Question and Answers Forum

All Questions      Topic List

Integration Questions

Previous in All Question      Next in All Question      

Previous in Integration      Next in Integration      

Question Number 134239 by ruwedkabeh last updated on 01/Mar/21

$$caniaskforsomehelp?$$ $$howtoprovethis?$$ $$\frac{1}{2}<\underset{0}{\stackrel{\frac{1}{2}}{\int }}\frac{dx}{\sqrt{1-x^3}}<\frac{\pi }{6}$$

Commented byDwaipayan Shikari last updated on 01/Mar/21

$$\frac{1}{\sqrt{1-x^3}}=\underset{n=0}{\sum ^{\mathrm{\infty }}}\frac{{\left(\frac{1}{2}\right)}_n}{n!}{x}^{3n}{\left(a\right)}_n=a(a+1)(a+2)...(a+n-1)$$ $${\int }_0^{\frac{1}{2}}\frac{1}{\sqrt{1-x^3}}dx=\underset{n=0}{\sum ^{\mathrm{\infty }}}\frac{{\left(\frac{1}{2}\right)}_n}{n!(3n+1)}{\left(\frac{1}{2}\right)}^{3n+1}$$ $$=\frac{1}{6}\underset{n=0}{\sum ^{\mathrm{\infty }}}\frac{{\left(\frac{1}{2}\right)}_n}{n!(n+\frac{1}{3})}{\left(\frac{1}{8}\right)}^n=\frac{1}{6}\underset{n=0}{\sum ^{\mathrm{\infty }}}\frac{{\left(\frac{1}{2}\right)}_n{\left(\frac{1}{3}\right)}_n}{n!{\left(\frac{4}{3}\right)}_n}{\left(\frac{1}{8}\right)}^n$$ $$=\frac{1}{6}{}_2{F}_1(\frac{1}{2},\frac{1}{3};\frac{4}{3};\frac{1}{8})$$ $$So\frac{1}{2}<\frac{1}{6}{}_2{F}_1(\frac{1}{2},\frac{1}{3};\frac{4}{3};\frac{1}{8})<\frac{\pi }{6}$$ $$3{<}_2{F}_1(\frac{1}{2},\frac{1}{3};\frac{4}{3};\frac{1}{8})<\pi$$

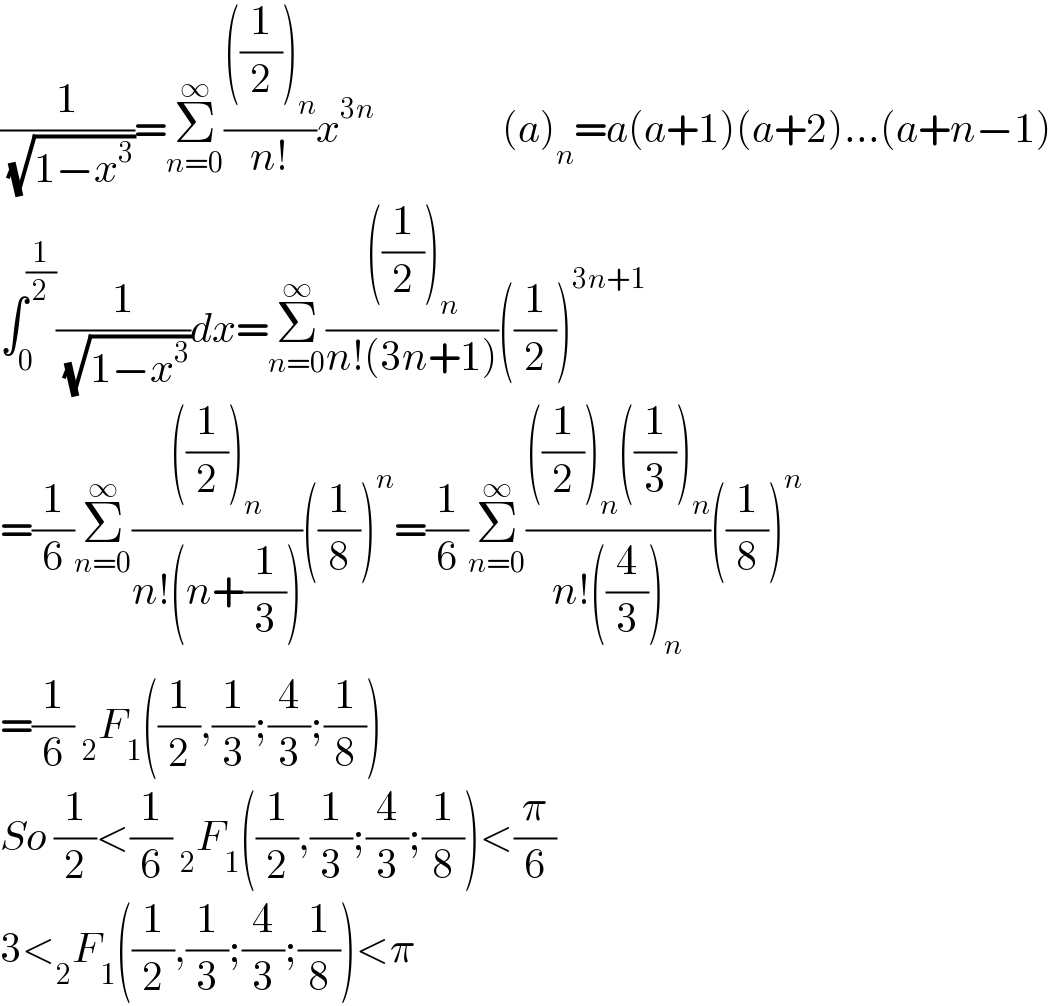
Commented byruwedkabeh last updated on 01/Mar/21

$$thankyousomuch$$

Answered by mr W last updated on 01/Mar/21

$$for0⩽x⩽\frac{1}{2}:$$ $$0<x^3<x^2$$ $$1-x^2<1-x^3<1$$ $$\sqrt{1-x^2}<\sqrt{1-x^3}<1$$ $$1<\frac{1}{\sqrt{1-x^3}}<\frac{1}{\sqrt{1-x^2}}$$ $${\int }_0^{\frac{1}{2}}1dx<{\int }_0^{\frac{1}{2}}\frac{1}{\sqrt{1-x^3}}dx<{\int }_0^{\frac{1}{2}}\frac{1}{\sqrt{1-x^2}}dx$$ $$1\times \frac{1}{2}<{\int }_0^{\frac{1}{2}}\frac{1}{\sqrt{1-x^3}}dx<{\left[{\sin }^{-1}x\right]}_0^{\frac{1}{2}}$$ $$\frac{1}{2}<{\int }_0^{\frac{1}{2}}\frac{dx}{\sqrt{1-x^3}}<\frac{\pi }{6}$$

Commented byruwedkabeh last updated on 01/Mar/21

$$thankyousomuch$$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com