Question and Answers Forum

All Questions      Topic List

None Questions

Previous in All Question      Next in All Question      

Previous in None      Next in None      

Question Number 134378 by mohammad17 last updated on 02/Mar/21

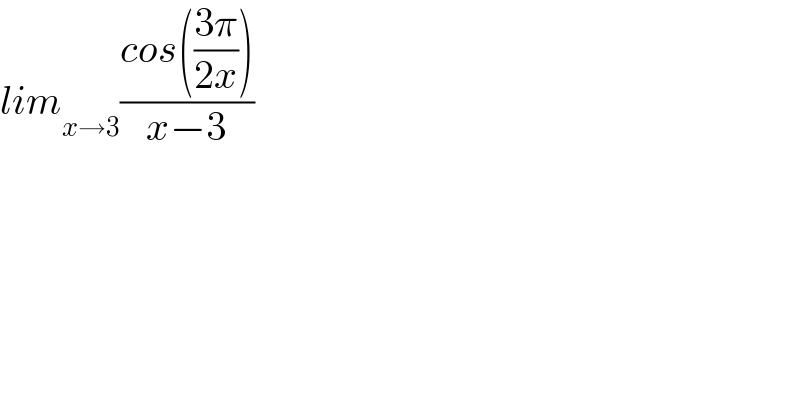
lim_(x→3) ((cos(((3π)/(2x))))/(x−3))

$${lim}_{{x}\rightarrow\mathrm{3}} \frac{{cos}\left(\frac{\mathrm{3}\pi}{\mathrm{2}{x}}\right)}{{x}−\mathrm{3}} \\ $$

Answered by bramlexs22 last updated on 02/Mar/21

lim_(x−3→0) ((cos (((3π)/(2x))))/(x−3)) let x−3=w ⇒ (1/x)=(1/(w+3)) lim_(w→0) ((cos (((3π)/(2(w+3)))))/w) = lim_(w→0) ((((3π)/(2(w+3)^2 )).sin (((3π)/(2(w+3)))))/1) = (π/6)

$$\underset{{x}−\mathrm{3}\rightarrow\mathrm{0}} {\mathrm{lim}}\:\frac{\mathrm{cos}\:\left(\frac{\mathrm{3}\pi}{\mathrm{2x}}\right)}{\mathrm{x}−\mathrm{3}} \\ $$$$\mathrm{let}\:\mathrm{x}−\mathrm{3}=\mathrm{w}\:\Rightarrow\:\frac{\mathrm{1}}{\mathrm{x}}=\frac{\mathrm{1}}{\mathrm{w}+\mathrm{3}} \\ $$$$\underset{\mathrm{w}\rightarrow\mathrm{0}} {\mathrm{lim}}\:\frac{\mathrm{cos}\:\left(\frac{\mathrm{3}\pi}{\mathrm{2}\left(\mathrm{w}+\mathrm{3}\right)}\right)}{\mathrm{w}}\:= \\ $$$$\underset{\mathrm{w}\rightarrow\mathrm{0}} {\mathrm{lim}}\:\frac{\frac{\mathrm{3}\pi}{\mathrm{2}\left(\mathrm{w}+\mathrm{3}\right)^{\mathrm{2}} }.\mathrm{sin}\:\left(\frac{\mathrm{3}\pi}{\mathrm{2}\left(\mathrm{w}+\mathrm{3}\right)}\right)}{\mathrm{1}}\:=\:\frac{\pi}{\mathrm{6}} \\ $$

Commented by mr W last updated on 03/Mar/21

((3π)/2)×(1/3^2 )

$$\frac{\mathrm{3}\pi}{\mathrm{2}}×\frac{\mathrm{1}}{\mathrm{3}^{\mathrm{2}} } \\ $$

Commented by bramlexs22 last updated on 02/Mar/21

(d/dw) [cos (((3π)/(2(w+3))))]= (d/dw) [cos ((3π)/2)(w+3)^(−1) ]= −((3π)/2).(w+3)^(−2) [−sin (((3π)/(2(w+3))))] lim_(w→0) ((3π)/(2(w+3)^2 )).sin (((3π)/(2(w+3))))= ((3π)/(18))×1=(π/6)

$$\frac{\mathrm{d}}{\mathrm{dw}}\:\left[\mathrm{cos}\:\left(\frac{\mathrm{3}\pi}{\mathrm{2}\left(\mathrm{w}+\mathrm{3}\right)}\right)\right]= \\ $$$$\frac{\mathrm{d}}{\mathrm{dw}}\:\left[\mathrm{cos}\:\frac{\mathrm{3}\pi}{\mathrm{2}}\left(\mathrm{w}+\mathrm{3}\right)^{−\mathrm{1}} \:\right]= \\ $$$$−\frac{\mathrm{3}\pi}{\mathrm{2}}.\left(\mathrm{w}+\mathrm{3}\right)^{−\mathrm{2}} \:\left[−\mathrm{sin}\:\left(\frac{\mathrm{3}\pi}{\mathrm{2}\left(\mathrm{w}+\mathrm{3}\right)}\right)\right] \\ $$$$\underset{\mathrm{w}\rightarrow\mathrm{0}} {\mathrm{lim}}\:\:\frac{\mathrm{3}\pi}{\mathrm{2}\left(\mathrm{w}+\mathrm{3}\right)^{\mathrm{2}} }.\mathrm{sin}\:\left(\frac{\mathrm{3}\pi}{\mathrm{2}\left(\mathrm{w}+\mathrm{3}\right)}\right)= \\ $$$$\frac{\mathrm{3}\pi}{\mathrm{18}}×\mathrm{1}=\frac{\pi}{\mathrm{6}} \\ $$

Answered by mathmax by abdo last updated on 02/Mar/21

f(x)=((cos(((3π)/(2x))))/(x−3)) changement ((3π)/(2x))=(π/2)+t x→3 ⇒t→0 and ((3π)/(2x))=((2t+π)/2) ⇒((3π)/x)=2t+π ⇒(x/(3π))=(1/(2t+π)) ⇒ x=((3π)/(2t+π)) ⇒x−3=((3π)/(2t+π))−3 =((3π−6t−3π)/(2t+π)) =((−6t)/(2t+π)) ⇒ f(x)=g(t)=((cos((π/2)+t))/((−6t)/(2t+π))) =(((2t+π)sint)/(6t)) ⇒g(t)∼((2t+π)/6) →(π/6) ⇒ lim_(x→3) f(x)=(π/6)

$$\mathrm{f}\left(\mathrm{x}\right)=\frac{\mathrm{cos}\left(\frac{\mathrm{3}\pi}{\mathrm{2x}}\right)}{\mathrm{x}−\mathrm{3}}\:\:\mathrm{changement}\:\frac{\mathrm{3}\pi}{\mathrm{2x}}=\frac{\pi}{\mathrm{2}}+\mathrm{t} \\ $$$$\mathrm{x}\rightarrow\mathrm{3}\:\Rightarrow\mathrm{t}\rightarrow\mathrm{0}\:\mathrm{and}\:\frac{\mathrm{3}\pi}{\mathrm{2x}}=\frac{\mathrm{2t}+\pi}{\mathrm{2}}\:\Rightarrow\frac{\mathrm{3}\pi}{\mathrm{x}}=\mathrm{2t}+\pi\:\Rightarrow\frac{\mathrm{x}}{\mathrm{3}\pi}=\frac{\mathrm{1}}{\mathrm{2t}+\pi}\:\Rightarrow \\ $$$$\mathrm{x}=\frac{\mathrm{3}\pi}{\mathrm{2t}+\pi}\:\Rightarrow\mathrm{x}−\mathrm{3}=\frac{\mathrm{3}\pi}{\mathrm{2t}+\pi}−\mathrm{3}\:=\frac{\mathrm{3}\pi−\mathrm{6t}−\mathrm{3}\pi}{\mathrm{2t}+\pi}\:=\frac{−\mathrm{6t}}{\mathrm{2t}+\pi}\:\Rightarrow \\ $$$$\mathrm{f}\left(\mathrm{x}\right)=\mathrm{g}\left(\mathrm{t}\right)=\frac{\mathrm{cos}\left(\frac{\pi}{\mathrm{2}}+\mathrm{t}\right)}{\frac{−\mathrm{6t}}{\mathrm{2t}+\pi}}\:=\frac{\left(\mathrm{2t}+\pi\right)\mathrm{sint}}{\mathrm{6t}}\:\Rightarrow\mathrm{g}\left(\mathrm{t}\right)\sim\frac{\mathrm{2t}+\pi}{\mathrm{6}}\:\rightarrow\frac{\pi}{\mathrm{6}}\:\Rightarrow \\ $$$$\mathrm{lim}_{\mathrm{x}\rightarrow\mathrm{3}} \mathrm{f}\left(\mathrm{x}\right)=\frac{\pi}{\mathrm{6}} \\ $$$$ \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com