
Question and Answers Forum
Question Number 134391 by bramlexs22 last updated on 03/Mar/21
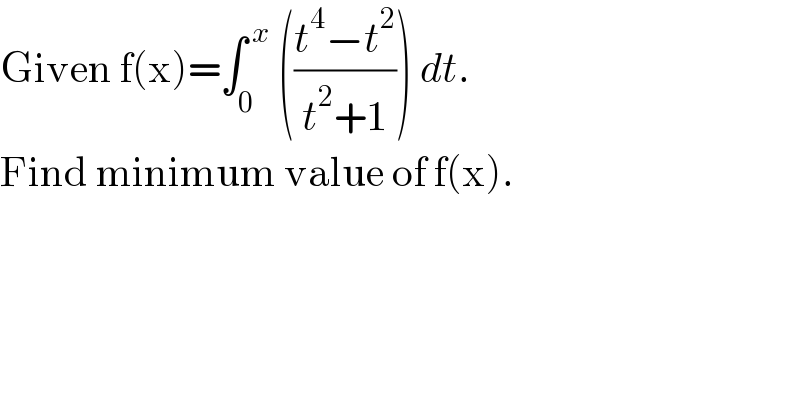
Answered by liberty last updated on 03/Mar/21
![Given f(x) = ∫_0 ^( x) [ ((t^4 −t^2 )/(t^2 +1))] dt. Find minimum value of f(x). (•) ((df(x))/dx) = ((x^4 −x^2 )/(x^2 +1)) = 0 x^2 (x−1) = 0 → { ((x=0)),((x=1)) :} (••) ((d^2 f(x))/dx^2 )∣_(x=1) = (((4x^3 −2x)(x^2 +1)−2x(x^4 −x^2 ))/((x^2 +1)^2 ))>0 for x=1 so minimum value is f(1) (•••) f(1)=∫_0 ^( 1) ((t^4 −t^2 )/(t^2 +1)) dt f(1)=∫_0 ^( 1) (t^2 −2+ (2/(t^2 +1)))dt f(1)= [(t^3 /3)−2t+2arctan t ]_0 ^1 f(1)= (1/3)−2+2((π/4))= (π/2)−(5/6)](Q134392.png)
| ||
Question and Answers Forum | ||
Question Number 134391 by bramlexs22 last updated on 03/Mar/21 | ||
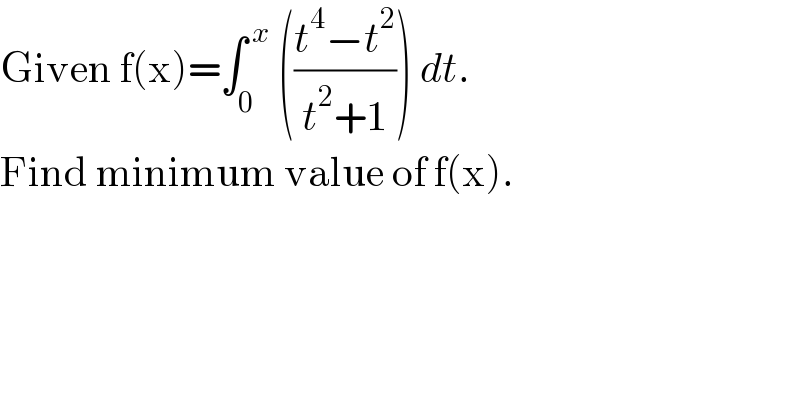 | ||
Answered by liberty last updated on 03/Mar/21 | ||
![Given f(x) = ∫_0 ^( x) [ ((t^4 −t^2 )/(t^2 +1))] dt. Find minimum value of f(x). (•) ((df(x))/dx) = ((x^4 −x^2 )/(x^2 +1)) = 0 x^2 (x−1) = 0 → { ((x=0)),((x=1)) :} (••) ((d^2 f(x))/dx^2 )∣_(x=1) = (((4x^3 −2x)(x^2 +1)−2x(x^4 −x^2 ))/((x^2 +1)^2 ))>0 for x=1 so minimum value is f(1) (•••) f(1)=∫_0 ^( 1) ((t^4 −t^2 )/(t^2 +1)) dt f(1)=∫_0 ^( 1) (t^2 −2+ (2/(t^2 +1)))dt f(1)= [(t^3 /3)−2t+2arctan t ]_0 ^1 f(1)= (1/3)−2+2((π/4))= (π/2)−(5/6)](Q134392.png) | ||
| ||