Question and Answers Forum

All Questions      Topic List

None Questions

Previous in All Question      Next in All Question      

Previous in None      Next in None      

Question Number 134615 by mathocean1 last updated on 05/Mar/21

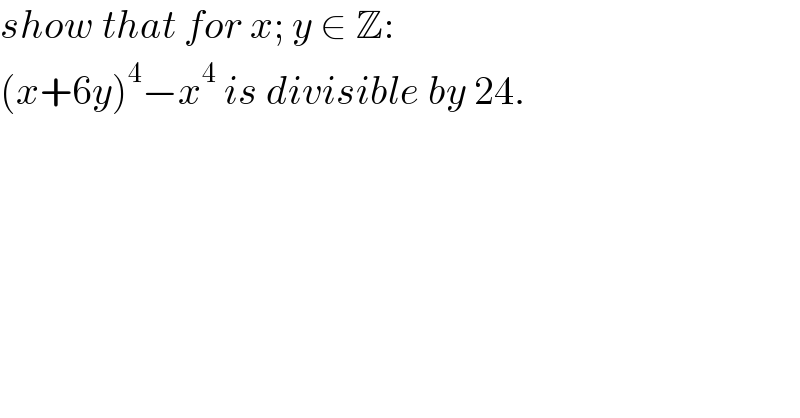
show that for x; y ∈ Z: (x+6y)^4 −x^4 is divisible by 24.

$${show}\:{that}\:{for}\:{x};\:{y}\:\in\:\mathbb{Z}: \\ $$$$\left({x}+\mathrm{6}{y}\right)^{\mathrm{4}} −{x}^{\mathrm{4}} \:{is}\:{divisible}\:{by}\:\mathrm{24}. \\ $$

Answered by Olaf last updated on 05/Mar/21

Let X = (x+6y)^4 −x^4 X = (x+6y−x)[(x+6y)^3 +x(x+6y)^2 +x^2 (x+6y)+x^3 ] X = 6y[(x+6y)^3 +x(x+6y)^2 +x^2 (x+6y)+x^3 ] ⇒ X is divisible by 6, X = 6Y Y = (x+6y)^3 +x(x+6y)^2 +x^2 (x+6y)+x^3 Y = (x^3 +18x^2 y+108xy^2 +196y^3 ) +(x^3 +12x^2 y+36xy^2 )+(x^3 +6x^2 y)+x^3 Y = 4(x^3 +9x^2 y+36xy^2 +49y^3 ) ⇒ Y is divisible by 4, Y = 4p Finally, X = 6Y = 24p ⇒ X is divisible by 24

$$\mathrm{Let}\:\mathrm{X}\:=\:\left({x}+\mathrm{6}{y}\right)^{\mathrm{4}} −{x}^{\mathrm{4}} \\ $$$$\mathrm{X}\:=\:\left({x}+\mathrm{6}{y}−{x}\right)\left[\left({x}+\mathrm{6}{y}\right)^{\mathrm{3}} +{x}\left({x}+\mathrm{6}{y}\right)^{\mathrm{2}} +{x}^{\mathrm{2}} \left({x}+\mathrm{6}{y}\right)+{x}^{\mathrm{3}} \right] \\ $$$$\mathrm{X}\:=\:\mathrm{6}{y}\left[\left({x}+\mathrm{6}{y}\right)^{\mathrm{3}} +{x}\left({x}+\mathrm{6}{y}\right)^{\mathrm{2}} +{x}^{\mathrm{2}} \left({x}+\mathrm{6}{y}\right)+{x}^{\mathrm{3}} \right] \\ $$$$\Rightarrow\:\mathrm{X}\:\mathrm{is}\:\mathrm{divisible}\:\mathrm{by}\:\mathrm{6},\:\mathrm{X}\:=\:\mathrm{6Y} \\ $$$$ \\ $$$$\mathrm{Y}\:=\:\left({x}+\mathrm{6}{y}\right)^{\mathrm{3}} +{x}\left({x}+\mathrm{6}{y}\right)^{\mathrm{2}} +{x}^{\mathrm{2}} \left({x}+\mathrm{6}{y}\right)+{x}^{\mathrm{3}} \\ $$$$\mathrm{Y}\:=\:\left({x}^{\mathrm{3}} +\mathrm{18}{x}^{\mathrm{2}} {y}+\mathrm{108}{xy}^{\mathrm{2}} +\mathrm{196}{y}^{\mathrm{3}} \right) \\ $$$$+\left({x}^{\mathrm{3}} +\mathrm{12}{x}^{\mathrm{2}} {y}+\mathrm{36}{xy}^{\mathrm{2}} \right)+\left({x}^{\mathrm{3}} +\mathrm{6}{x}^{\mathrm{2}} {y}\right)+{x}^{\mathrm{3}} \\ $$$$\mathrm{Y}\:=\:\mathrm{4}\left({x}^{\mathrm{3}} +\mathrm{9}{x}^{\mathrm{2}} {y}+\mathrm{36}{xy}^{\mathrm{2}} +\mathrm{49}{y}^{\mathrm{3}} \right) \\ $$$$\Rightarrow\:\mathrm{Y}\:\mathrm{is}\:\mathrm{divisible}\:\mathrm{by}\:\mathrm{4},\:\mathrm{Y}\:=\:\mathrm{4}{p} \\ $$$$ \\ $$$$\mathrm{Finally},\:\mathrm{X}\:=\:\mathrm{6Y}\:=\:\mathrm{24}{p} \\ $$$$\Rightarrow\:\mathrm{X}\:\mathrm{is}\:\mathrm{divisible}\:\mathrm{by}\:\mathrm{24} \\ $$

Answered by Rasheed.Sindhi last updated on 06/Mar/21

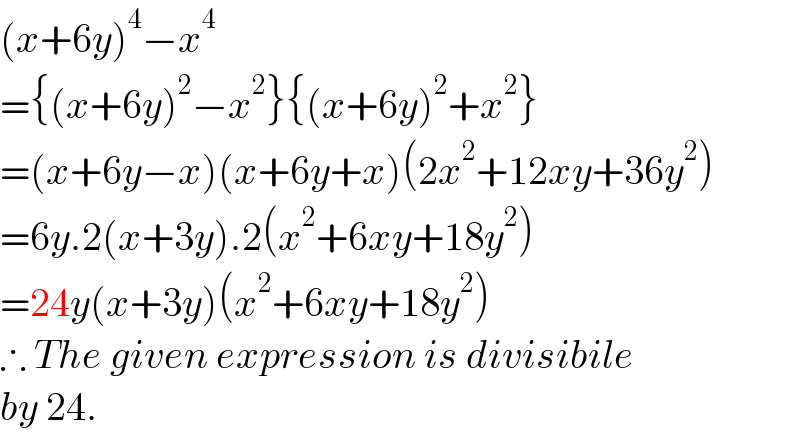
(x+6y)^4 −x^4 ={(x+6y)^2 −x^2 }{(x+6y)^2 +x^2 } =(x+6y−x)(x+6y+x)(2x^2 +12xy+36y^2 ) =6y.2(x+3y).2(x^2 +6xy+18y^2 ) =24y(x+3y)(x^2 +6xy+18y^2 ) ∴ The given expression is divisibile by 24.

$$\left({x}+\mathrm{6}{y}\right)^{\mathrm{4}} −{x}^{\mathrm{4}} \\ $$$$=\left\{\left({x}+\mathrm{6}{y}\right)^{\mathrm{2}} −{x}^{\mathrm{2}} \right\}\left\{\left({x}+\mathrm{6}{y}\right)^{\mathrm{2}} +{x}^{\mathrm{2}} \right\} \\ $$$$=\left({x}+\mathrm{6}{y}−{x}\right)\left({x}+\mathrm{6}{y}+{x}\right)\left(\mathrm{2}{x}^{\mathrm{2}} +\mathrm{12}{xy}+\mathrm{36}{y}^{\mathrm{2}} \right) \\ $$$$=\mathrm{6}{y}.\mathrm{2}\left({x}+\mathrm{3}{y}\right).\mathrm{2}\left({x}^{\mathrm{2}} +\mathrm{6}{xy}+\mathrm{18}{y}^{\mathrm{2}} \right) \\ $$$$=\mathrm{24}{y}\left({x}+\mathrm{3}{y}\right)\left({x}^{\mathrm{2}} +\mathrm{6}{xy}+\mathrm{18}{y}^{\mathrm{2}} \right) \\ $$$$\therefore\:{The}\:{given}\:{expression}\:{is}\:{divisibile} \\ $$$${by}\:\mathrm{24}. \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com