Question and Answers Forum

All Questions      Topic List

Integration Questions

Previous in All Question      Next in All Question      

Previous in Integration      Next in Integration      

Question Number 134636 by bobhans last updated on 06/Mar/21

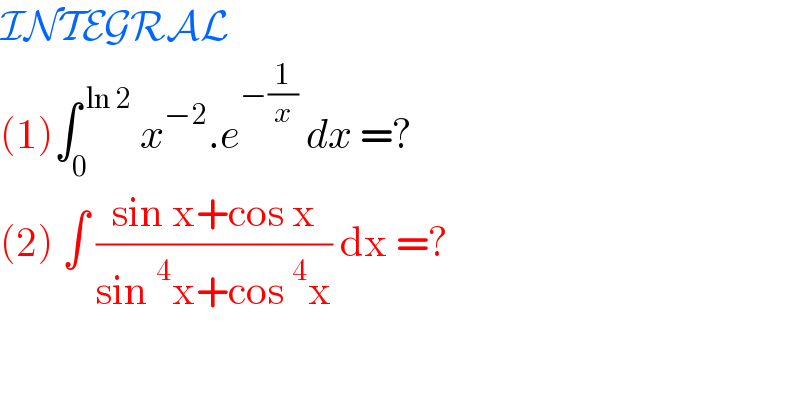
INTEGRAL (1)∫_0 ^( ln 2) x^(−2) .e^(−(1/x)) dx =? (2) ∫ ((sin x+cos x)/(sin^4 x+cos^4 x)) dx =?

$$\mathcal{INTEGRAL} \\ $$$$\left(\mathrm{1}\right)\int_{\mathrm{0}} ^{\:\mathrm{ln}\:\mathrm{2}} \:{x}^{−\mathrm{2}} .{e}^{−\frac{\mathrm{1}}{{x}}} \:{dx}\:=? \\ $$$$\left(\mathrm{2}\right)\:\int\:\frac{\mathrm{sin}\:\mathrm{x}+\mathrm{cos}\:\mathrm{x}}{\mathrm{sin}\:^{\mathrm{4}} \mathrm{x}+\mathrm{cos}\:^{\mathrm{4}} \mathrm{x}}\:\mathrm{dx}\:=? \\ $$

Answered by benjo_mathlover last updated on 06/Mar/21

(1) ∫_0 ^(ln 2) (e^(−(1/x)) /x^2 ) dx = ∫_0 ^(ln 2) e^(−(1/x)) d(−(1/x)) = lim_(p→0) [ e^(−(1/x)) ]_p ^(ln 2) = e^(−(1/(ln 2))) −e^(−∞) = e^(−(1/(ln 2))) = (1/( (( e))^(1/(ln 2 )) ))

$$\left(\mathrm{1}\right)\:\int_{\mathrm{0}} ^{\mathrm{ln}\:\mathrm{2}} \:\frac{\mathrm{e}^{−\frac{\mathrm{1}}{\mathrm{x}}} }{\mathrm{x}^{\mathrm{2}} }\:\mathrm{dx}\:=\:\int_{\mathrm{0}} ^{\mathrm{ln}\:\mathrm{2}} \:\mathrm{e}^{−\frac{\mathrm{1}}{\mathrm{x}}} \:\mathrm{d}\left(−\frac{\mathrm{1}}{\mathrm{x}}\right) \\ $$$$=\:\underset{\mathrm{p}\rightarrow\mathrm{0}} {\mathrm{lim}}\:\left[\:\mathrm{e}^{−\frac{\mathrm{1}}{\mathrm{x}}} \:\right]_{\mathrm{p}} ^{\mathrm{ln}\:\mathrm{2}} =\:\mathrm{e}^{−\frac{\mathrm{1}}{\mathrm{ln}\:\mathrm{2}}} −\mathrm{e}^{−\infty} \\ $$$$=\:\mathrm{e}^{−\frac{\mathrm{1}}{\mathrm{ln}\:\mathrm{2}}} \:=\:\frac{\mathrm{1}}{\:\sqrt[{\mathrm{ln}\:\mathrm{2}\:}]{\:\mathrm{e}}}\: \\ $$

Answered by rs4089 last updated on 06/Mar/21

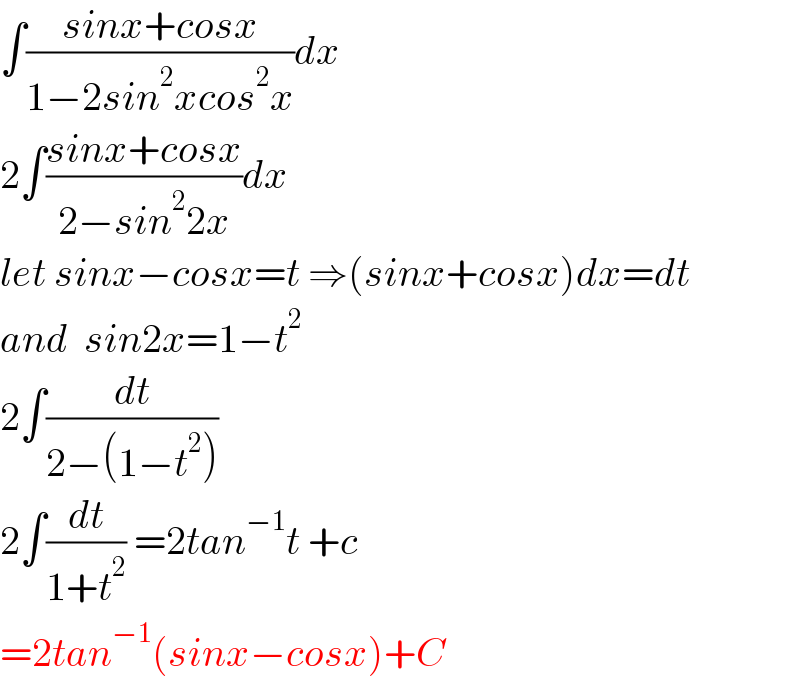
∫((sinx+cosx)/(1−2sin^2 xcos^2 x))dx 2∫((sinx+cosx)/(2−sin^2 2x))dx let sinx−cosx=t ⇒(sinx+cosx)dx=dt and sin2x=1−t^2 2∫(dt/(2−(1−t^2 ))) 2∫(dt/(1+t^2 )) =2tan^(−1) t +c =2tan^(−1) (sinx−cosx)+C

$$\int\frac{{sinx}+{cosx}}{\mathrm{1}−\mathrm{2}{sin}^{\mathrm{2}} {xcos}^{\mathrm{2}} {x}}{dx} \\ $$$$\mathrm{2}\int\frac{{sinx}+{cosx}}{\mathrm{2}−{sin}^{\mathrm{2}} \mathrm{2}{x}}{dx} \\ $$$${let}\:{sinx}−{cosx}={t}\:\Rightarrow\left({sinx}+{cosx}\right){dx}={dt} \\ $$$${and}\:\:{sin}\mathrm{2}{x}=\mathrm{1}−{t}^{\mathrm{2}} \\ $$$$\mathrm{2}\int\frac{{dt}}{\mathrm{2}−\left(\mathrm{1}−{t}^{\mathrm{2}} \right)} \\ $$$$\mathrm{2}\int\frac{{dt}}{\mathrm{1}+{t}^{\mathrm{2}} }\:=\mathrm{2}{tan}^{−\mathrm{1}} {t}\:+{c} \\ $$$$=\mathrm{2}{tan}^{−\mathrm{1}} \left({sinx}−{cosx}\right)+{C} \\ $$

Answered by john_santu last updated on 06/Mar/21

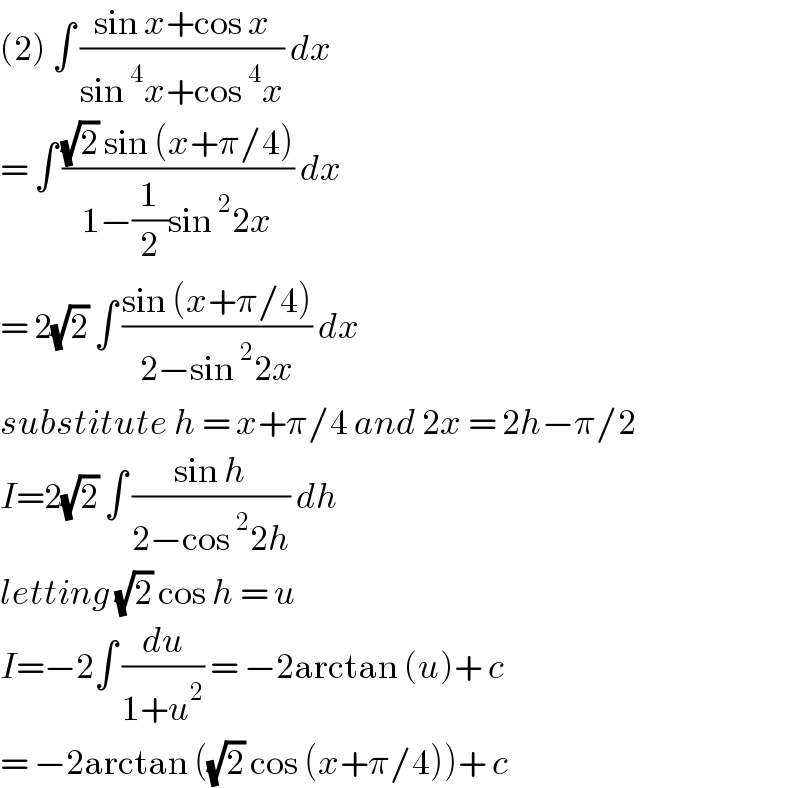
(2) ∫ ((sin x+cos x)/(sin^4 x+cos^4 x)) dx = ∫ (((√2) sin (x+π/4))/(1−(1/2)sin^2 2x)) dx = 2(√2) ∫ ((sin (x+π/4))/(2−sin^2 2x)) dx substitute h = x+π/4 and 2x = 2h−π/2 I=2(√2) ∫ ((sin h)/(2−cos^2 2h)) dh letting (√2) cos h = u I=−2∫ (du/(1+u^2 )) = −2arctan (u)+ c = −2arctan ((√2) cos (x+π/4))+ c

$$\left(\mathrm{2}\right)\:\int\:\frac{\mathrm{sin}\:{x}+\mathrm{cos}\:{x}}{\mathrm{sin}\:^{\mathrm{4}} {x}+\mathrm{cos}\:^{\mathrm{4}} {x}}\:{dx}\: \\ $$$$=\:\int\:\frac{\sqrt{\mathrm{2}}\:\mathrm{sin}\:\left({x}+\pi/\mathrm{4}\right)}{\mathrm{1}−\frac{\mathrm{1}}{\mathrm{2}}\mathrm{sin}\:^{\mathrm{2}} \mathrm{2}{x}}\:{dx} \\ $$$$=\:\mathrm{2}\sqrt{\mathrm{2}}\:\int\:\frac{\mathrm{sin}\:\left({x}+\pi/\mathrm{4}\right)}{\mathrm{2}−\mathrm{sin}\:^{\mathrm{2}} \mathrm{2}{x}}\:{dx} \\ $$$${substitute}\:{h}\:=\:{x}+\pi/\mathrm{4}\:{and}\:\mathrm{2}{x}\:=\:\mathrm{2}{h}−\pi/\mathrm{2} \\ $$$${I}=\mathrm{2}\sqrt{\mathrm{2}}\:\int\:\frac{\mathrm{sin}\:{h}}{\mathrm{2}−\mathrm{cos}\:^{\mathrm{2}} \mathrm{2}{h}}\:{dh} \\ $$$${letting}\:\sqrt{\mathrm{2}}\:\mathrm{cos}\:{h}\:=\:{u}\: \\ $$$${I}=−\mathrm{2}\int\:\frac{{du}}{\mathrm{1}+{u}^{\mathrm{2}} }\:=\:−\mathrm{2arctan}\:\left({u}\right)+\:{c} \\ $$$$=\:−\mathrm{2arctan}\:\left(\sqrt{\mathrm{2}}\:\mathrm{cos}\:\left({x}+\pi/\mathrm{4}\right)\right)+\:{c}\: \\ $$

Answered by mathmax by abdo last updated on 27/Mar/21

1) we have (d/dx)(e^(−(1/x)) ) =(1/x^2 )e^(−(1/x)) ⇒ ∫_0 ^(ln2) x^(−2) e^(−(1/x)) ex =[e^(−(1/x)) ]_0 ^(ln2) =e^(−(1/(ln2))) −0 =e^(−(1/(ln2)))

$$\left.\mathrm{1}\right)\:\mathrm{we}\:\mathrm{have}\:\frac{\mathrm{d}}{\mathrm{dx}}\left(\mathrm{e}^{−\frac{\mathrm{1}}{\mathrm{x}}} \right)\:=\frac{\mathrm{1}}{\mathrm{x}^{\mathrm{2}} }\mathrm{e}^{−\frac{\mathrm{1}}{\mathrm{x}}} \:\Rightarrow \\ $$$$\int_{\mathrm{0}} ^{\mathrm{ln2}} \:\mathrm{x}^{−\mathrm{2}} \:\mathrm{e}^{−\frac{\mathrm{1}}{\mathrm{x}}} \:\mathrm{ex}\:=\left[\mathrm{e}^{−\frac{\mathrm{1}}{\mathrm{x}}} \right]_{\mathrm{0}} ^{\mathrm{ln2}} \:=\mathrm{e}^{−\frac{\mathrm{1}}{\mathrm{ln2}}} −\mathrm{0}\:=\mathrm{e}^{−\frac{\mathrm{1}}{\mathrm{ln2}}} \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com