Question and Answers Forum

All Questions      Topic List

Integration Questions

Previous in All Question      Next in All Question      

Previous in Integration      Next in Integration      

Question Number 134660 by benjo_mathlover last updated on 06/Mar/21

$$\mathcal{M}=\int \frac{dx}{2\cos x+3\sin x}$$

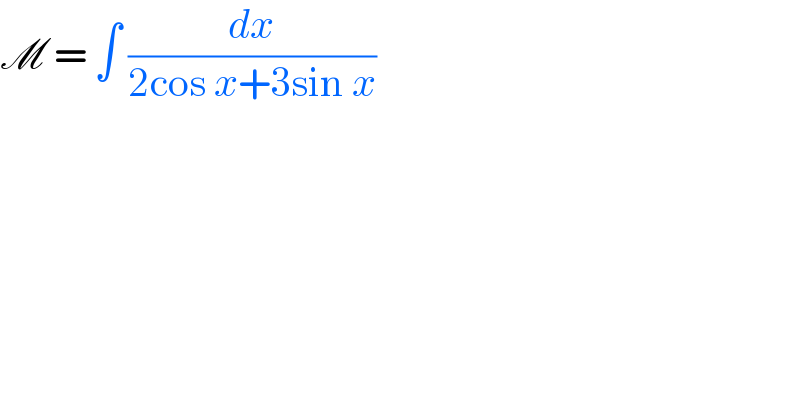
Answered by EDWIN88 last updated on 06/Mar/21

$$\mathrm{Let}\{\begin{array}{l}2=\mathrm{r}\sin \alpha \\ 3=\mathrm{r}\cos \alpha \end{array}\Rightarrow {\mathrm{r}}^2=13;\mathrm{r}=\sqrt{13}$$$$\mathrm{and}\tan \alpha =\frac{2}{3},\therefore \alpha ={\tan }^{-1}\left(\frac{2}{3}\right)$$$$\mathcal{M}=\frac{1}{\mathrm{r}}\int \frac{\mathrm{dx}}{\sin (\alpha +\mathrm{x})}=\frac{1}{\mathrm{r}}\int \mathrm{cosec}(\mathrm{x}+\alpha )\mathrm{dx}$$$$\mathcal{M}=\frac{1}{\mathrm{r}}\ln \left[\tan \frac{(\mathrm{x}+\alpha )}{2}\right]+\mathrm{c}$$$$\mathcal{M}=\frac{1}{\sqrt{13}}\ln \left[\tan (\frac{\mathrm{x}}{2}+\frac{1}{2}{\tan }^{-1}\left(\frac{2}{3}\right))\right]+\mathrm{c}$$

Answered by mathmax by abdo last updated on 07/Mar/21

$$\mathrm{M}=\int \frac{\mathrm{dx}}{2\mathrm{cosx}+3\mathrm{sinx}}\mathrm{we}\mathrm{do}\mathrm{the}\mathrm{changement}\tan \left(\frac{\mathrm{x}}{2}\right)=\mathrm{t}\Rightarrow$$$$\mathrm{M}=\int \frac{2\mathrm{dt}}{(1+{\mathrm{t}}^2)(2\frac{1-{\mathrm{t}}^2}{1+{\mathrm{t}}^2}+\frac{6\mathrm{t}}{1+{\mathrm{t}}^2})}=\int \frac{2\mathrm{dt}}{2(1-{\mathrm{t}}^2)+6\mathrm{t}}=\int \frac{\mathrm{dt}}{1-{\mathrm{t}}^2+3\mathrm{t}}$$$$=-\int \frac{\mathrm{dt}}{{\mathrm{t}}^2-3\mathrm{t}-1}$$$$\mathrm{\Delta }=9+4=13\Rightarrow {\mathrm{t}}_1=\frac{3+\sqrt{13}}{2}\mathrm{and}{\mathrm{t}}_2=\frac{3-\sqrt{13}}{2}\Rightarrow$$$$\mathrm{M}=-\int \frac{\mathrm{dt}}{(\mathrm{t}-{\mathrm{t}}_1)(\mathrm{t}-{\mathrm{t}}_2)}=-\frac{1}{{\mathrm{t}}_1-{\mathrm{t}}_2}\int (\frac{1}{\mathrm{t}-{\mathrm{t}}_1}-\frac{1}{\mathrm{t}-{\mathrm{t}}_2})\mathrm{dt}$$$$=-\frac{1}{\sqrt{13}}\ln \mid \frac{\mathrm{t}-{\mathrm{t}}_1}{\mathrm{t}-{\mathrm{t}}_2}\mid +\mathrm{C}=-\frac{1}{\sqrt{13}}\ln \mid \frac{\mathrm{t}-\frac{3+\sqrt{13}}{2}}{\mathrm{t}-\frac{3-\sqrt{13}}{2}}\mid +\mathrm{C}$$$$=-\frac{1}{\sqrt{13}}\ln \mid \frac{2\mathrm{t}-3-\sqrt{13}}{2\mathrm{t}-3+\sqrt{13}}\mid +\mathrm{C}$$

Commented by mathmax by abdo last updated on 07/Mar/21

$$\mathrm{t}=\tan \left(\frac{\mathrm{x}}{2}\right)\Rightarrow \mathrm{M}=-\frac{1}{\sqrt{13}}\ln \mid \frac{2\tan \left(\frac{\mathrm{x}}{2}\right)-3-\sqrt{13}}{2\tan \left(\frac{\mathrm{x}}{2}\right)-3+\sqrt{13}}\mid +\mathrm{C}$$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com