
Question and Answers Forum
Question Number 134670 by benjo_mathlover last updated on 06/Mar/21
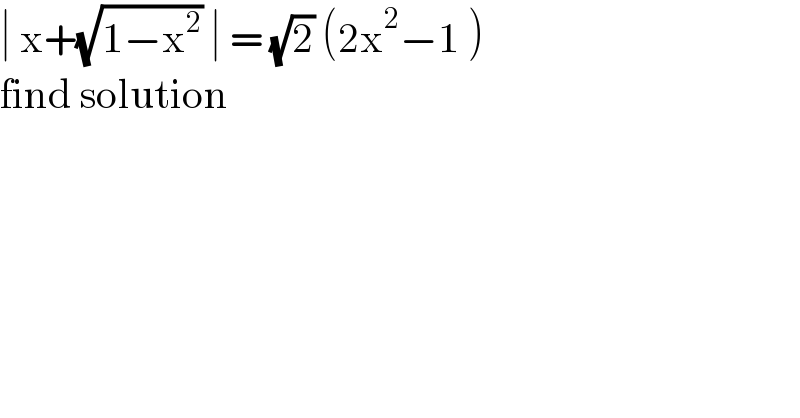
Answered by EDWIN88 last updated on 06/Mar/21
![(1) 1−x^2 ≥ 0 ⇒ −1≤x≤1 (2) let x = cos t ; t∈ [ 0,π ] ∣cos t +(√(1−cos^2 t)) ∣ =(√2) (2cos^2 t−1) ∣cos t +∣sin t∣∣ = (√2) cos 2t ∣ cos t+sin t ∣ = (√2) cos 2t (cos t+sin t)^2 = 2cos^2 2t ; { ((cos 2t ≥ 0)),((0≤t≤π)) :} (i) 1+sin 2t = 2−2sin^2 2t 2sin^2 2t +sin 2t−1 = 0→ { ((sin 2t=−1)),((sin 2t=(1/2))) :} { ((t=−(π/4)+kπ)),((t=(π/(12))+kπ ; t=((5π)/(12))+kπ)) :}→ t=(π/(12)) ; t=((3π)/4) { ((x = cos (π/(12))= (√((2+(√3))/4)) = ((√(2+(√3)))/2))),((x=cos ((3π)/4)=−((√2)/2))) :} therefore the solution is determinant (((x=((√(2+(√3)))/2))),((x =−((√2)/2))))](Q134674.png)
Commented by john_santu last updated on 06/Mar/21
![i think it should be t ∈ [ 0,2π ] then t = ((7π)/4) ∧ t = ((13π)/(12)) is the solution](Q134699.png)
Answered by benjo_mathlover last updated on 06/Mar/21
![∣x+(√(1−x^2 )) ∣ = (√2) (2x^2 −1) ⇒x+(√(1−x^2 )) = ±(√2) (2x^2 −1) ⇒(√(1−x^2 )) = −x±(√2)(2x^2 −1) squaring ⇒1−x^2 = x^2 ±2(√2) x(2x^2 −1)+2(2x^2 −1)^2 ⇒0 = 2x^2 −1±2(√2)x(2x^2 −1)+2(2x^2 −1)^2 ⇒0=(2x^2 −1)[1±2x(√2) +2(2x^2 −1)] (i) 2x^2 =1 ; x_(1,2) =± ((√2)/2) → { ((≈0.707)),((≈−0.707)) :} (ii) 4x^2 ±2(√2) x−1= 0 → { ((x_(3,4) = ((−2(√2) ± 2(√6))/8)=((−(√2) ±(√6))/4) { ((≈0.25)),((≈−0.965)) :})),((x_(5,6) = (((√2) ±(√6))/4) → { ((≈0.965)),((≈−0.25 )) :})) :} (iii)for (√(1−x^2 )) defined on −1≤x≤1 (iv) 2x^2 −1≥0 ; x≤−((√2)/2) ∪ x≥((√2)/2) solution is {±((√2)/2); ((−(√2) ±(√6))/4) ; (((√2) ±(√6))/4) }](Q134677.png)
| ||
Question and Answers Forum | ||
Question Number 134670 by benjo_mathlover last updated on 06/Mar/21 | ||
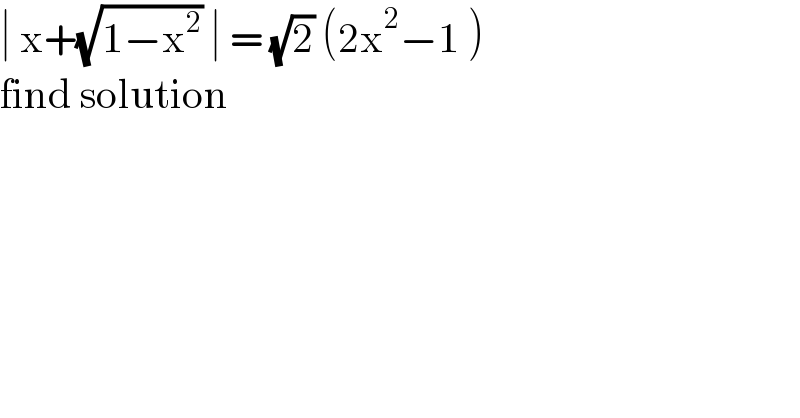 | ||
Answered by EDWIN88 last updated on 06/Mar/21 | ||
![(1) 1−x^2 ≥ 0 ⇒ −1≤x≤1 (2) let x = cos t ; t∈ [ 0,π ] ∣cos t +(√(1−cos^2 t)) ∣ =(√2) (2cos^2 t−1) ∣cos t +∣sin t∣∣ = (√2) cos 2t ∣ cos t+sin t ∣ = (√2) cos 2t (cos t+sin t)^2 = 2cos^2 2t ; { ((cos 2t ≥ 0)),((0≤t≤π)) :} (i) 1+sin 2t = 2−2sin^2 2t 2sin^2 2t +sin 2t−1 = 0→ { ((sin 2t=−1)),((sin 2t=(1/2))) :} { ((t=−(π/4)+kπ)),((t=(π/(12))+kπ ; t=((5π)/(12))+kπ)) :}→ t=(π/(12)) ; t=((3π)/4) { ((x = cos (π/(12))= (√((2+(√3))/4)) = ((√(2+(√3)))/2))),((x=cos ((3π)/4)=−((√2)/2))) :} therefore the solution is determinant (((x=((√(2+(√3)))/2))),((x =−((√2)/2))))](Q134674.png) | ||
| ||
Commented by john_santu last updated on 06/Mar/21 | ||
![i think it should be t ∈ [ 0,2π ] then t = ((7π)/4) ∧ t = ((13π)/(12)) is the solution](Q134699.png) | ||
Answered by benjo_mathlover last updated on 06/Mar/21 | ||
![∣x+(√(1−x^2 )) ∣ = (√2) (2x^2 −1) ⇒x+(√(1−x^2 )) = ±(√2) (2x^2 −1) ⇒(√(1−x^2 )) = −x±(√2)(2x^2 −1) squaring ⇒1−x^2 = x^2 ±2(√2) x(2x^2 −1)+2(2x^2 −1)^2 ⇒0 = 2x^2 −1±2(√2)x(2x^2 −1)+2(2x^2 −1)^2 ⇒0=(2x^2 −1)[1±2x(√2) +2(2x^2 −1)] (i) 2x^2 =1 ; x_(1,2) =± ((√2)/2) → { ((≈0.707)),((≈−0.707)) :} (ii) 4x^2 ±2(√2) x−1= 0 → { ((x_(3,4) = ((−2(√2) ± 2(√6))/8)=((−(√2) ±(√6))/4) { ((≈0.25)),((≈−0.965)) :})),((x_(5,6) = (((√2) ±(√6))/4) → { ((≈0.965)),((≈−0.25 )) :})) :} (iii)for (√(1−x^2 )) defined on −1≤x≤1 (iv) 2x^2 −1≥0 ; x≤−((√2)/2) ∪ x≥((√2)/2) solution is {±((√2)/2); ((−(√2) ±(√6))/4) ; (((√2) ±(√6))/4) }](Q134677.png) | ||
| ||