
Question and Answers Forum
Question Number 134708 by bramlexs22 last updated on 06/Mar/21
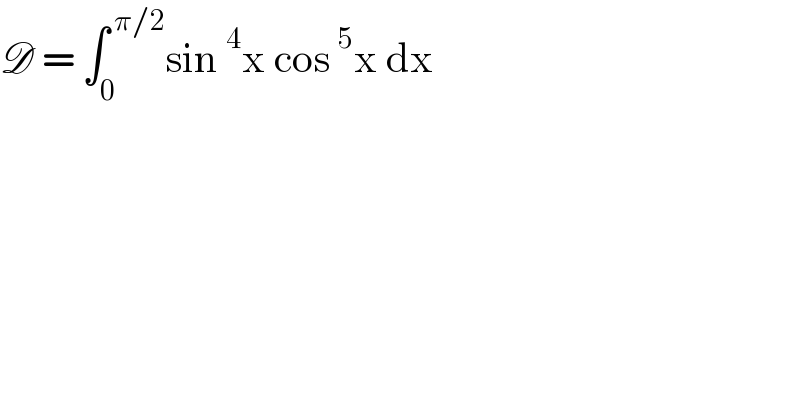
Answered by john_santu last updated on 06/Mar/21
![D = ∫_0 ^( π/2) sin^4 x(1−sin^2 x)^2 cos x dx let u= sin x , determinant (((u=1(upper limit))),((u=0 (lower limit)))) D = ∫_0 ^( 1) u^4 (u^4 −2u^2 +1) du D = ∫_0 ^( 1) (u^8 −2u^6 +u^4 )du D = [(u^9 /9)−((2u^7 )/7) +(u^5 /5) ]_0 ^1 D = (1/9)−(2/7)+(1/5) = ((35−90+63)/(315)) D = (8/(315)) •](Q134709.png)
Answered by Dwaipayan Shikari last updated on 06/Mar/21
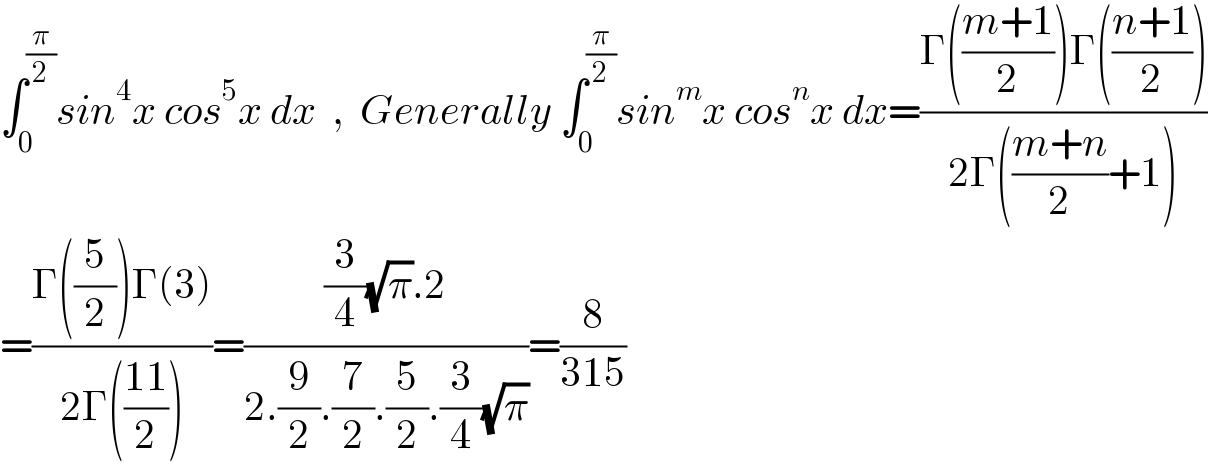
| ||
Question and Answers Forum | ||
Question Number 134708 by bramlexs22 last updated on 06/Mar/21 | ||
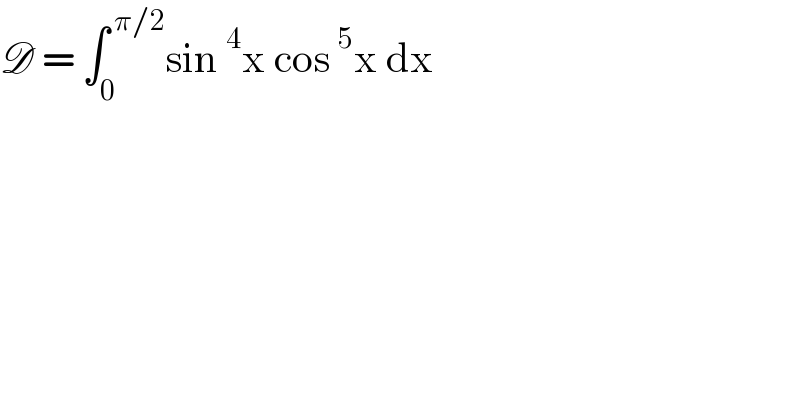 | ||
Answered by john_santu last updated on 06/Mar/21 | ||
![D = ∫_0 ^( π/2) sin^4 x(1−sin^2 x)^2 cos x dx let u= sin x , determinant (((u=1(upper limit))),((u=0 (lower limit)))) D = ∫_0 ^( 1) u^4 (u^4 −2u^2 +1) du D = ∫_0 ^( 1) (u^8 −2u^6 +u^4 )du D = [(u^9 /9)−((2u^7 )/7) +(u^5 /5) ]_0 ^1 D = (1/9)−(2/7)+(1/5) = ((35−90+63)/(315)) D = (8/(315)) •](Q134709.png) | ||
| ||
Answered by Dwaipayan Shikari last updated on 06/Mar/21 | ||
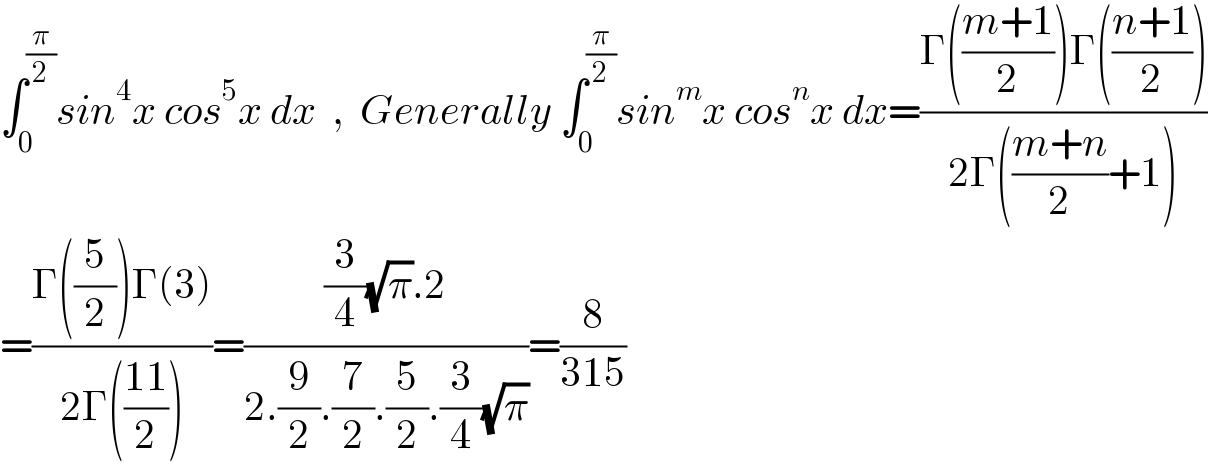 | ||
| ||