Question and Answers Forum

All Question   Topic List

Question Number 134772 by bramlexs22 last updated on 07/Mar/21

$$ \\ $$ What is the equation of a circle that goes through points (0,1), (1,4), and (5,2)?\\n

Commented bybramlexs22 last updated on 07/Mar/21

thank you all sir and master

$$\mathrm{thank}\:\mathrm{you}\:\mathrm{all}\:\mathrm{sir}\:\mathrm{and}\:\mathrm{master} \\ $$

Answered by EDWIN88 last updated on 07/Mar/21

The perpendicular bisector of any chord of a circle is a diameter and thus goes through the center of said circle Midpoint of { ((P_1 (0,1))),((P_2 (1,4))) :} is S((1/2),(5/2)) and the slope is m = ((4−1)/(1−0)) = 3, the perpendicular slope is m_p =−(1/3). the line equation ⇒y=−(1/3)(x−(1/2))+(5/2) ⇒y=−(1/3)x+(8/3) Midpoint of { ((P_2 (1,4))),((P_3 (5,2))) :}is Q(3,3) and the slope is m_2 =((4−2)/(1−5))=−(1/2),the perpendicular slope is m_p_2 = 2 , the line equation ⇒y=2(x−3)+3 ; y = 2x−3 set the two equation to find x and y, after solving we get { ((x= ((17)/7))),((y=((13)/7))) :} , so the center point is (((17)/7),((13)/7)) with radius =(√((0−((17)/7))^2 +(1−((13)/7))^2 )) r =(√((289+36)/(49))) = (√((325)/(49))) Therefore the circle′s equation is (x−((17)/7))^2 +(y−((13)/7))^2 = ((325)/(49))

$$\mathrm{\color{mathbrown}{T}\color{mathbrown}{h}\color{mathbrown}{e}}\color{mathbrown}{\:}\mathrm{\color{mathbrown}{p}\color{mathbrown}{e}\color{mathbrown}{r}\color{mathbrown}{p}\color{mathbrown}{e}\color{mathbrown}{n}\color{mathbrown}{d}\color{mathbrown}{i}\color{mathbrown}{c}\color{mathbrown}{u}\color{mathbrown}{l}\color{mathbrown}{a}\color{mathbrown}{r}}\color{mathbrown}{\:}\mathrm{\color{mathbrown}{b}\color{mathbrown}{i}\color{mathbrown}{s}\color{mathbrown}{e}\color{mathbrown}{c}\color{mathbrown}{t}\color{mathbrown}{o}\color{mathbrown}{r}}\color{mathbrown}{\:}\mathrm{\color{mathbrown}{o}\color{mathbrown}{f}}\color{mathbrown}{\:}\mathrm{\color{mathbrown}{a}\color{mathbrown}{n}\color{mathbrown}{y}}\color{mathbrown}{\:}\mathrm{\color{mathbrown}{c}\color{mathbrown}{h}\color{mathbrown}{o}\color{mathbrown}{r}\color{mathbrown}{d}}\color{mathbrown}{\:} \\ $$ $$\mathrm{\color{mathbrown}{o}\color{mathbrown}{f}}\color{mathbrown}{\:}\mathrm{\color{mathbrown}{a}}\color{mathbrown}{\:}\mathrm{\color{mathbrown}{c}\color{mathbrown}{i}\color{mathbrown}{r}\color{mathbrown}{c}\color{mathbrown}{l}\color{mathbrown}{e}}\color{mathbrown}{\:}\mathrm{\color{mathbrown}{i}\color{mathbrown}{s}}\color{mathbrown}{\:}\mathrm{\color{mathbrown}{a}}\color{mathbrown}{\:}\mathrm{\color{mathbrown}{d}\color{mathbrown}{i}\color{mathbrown}{a}\color{mathbrown}{m}\color{mathbrown}{e}\color{mathbrown}{t}\color{mathbrown}{e}\color{mathbrown}{r}}\color{mathbrown}{\:}\mathrm{\color{mathbrown}{a}\color{mathbrown}{n}\color{mathbrown}{d}}\color{mathbrown}{\:}\mathrm{\color{mathbrown}{t}\color{mathbrown}{h}\color{mathbrown}{u}\color{mathbrown}{s}}\color{mathbrown}{\:}\mathrm{\color{mathbrown}{g}\color{mathbrown}{o}\color{mathbrown}{e}\color{mathbrown}{s}}\color{mathbrown}{\:}\mathrm{\color{mathbrown}{t}\color{mathbrown}{h}\color{mathbrown}{r}\color{mathbrown}{o}\color{mathbrown}{u}\color{mathbrown}{g}\color{mathbrown}{h}} \\ $$ $$\mathrm{\color{mathbrown}{t}\color{mathbrown}{h}\color{mathbrown}{e}}\color{mathbrown}{\:}\mathrm{\color{mathbrown}{c}\color{mathbrown}{e}\color{mathbrown}{n}\color{mathbrown}{t}\color{mathbrown}{e}\color{mathbrown}{r}}\color{mathbrown}{\:}\mathrm{\color{mathbrown}{o}\color{mathbrown}{f}}\color{mathbrown}{\:}\mathrm{\color{mathbrown}{s}\color{mathbrown}{a}\color{mathbrown}{i}\color{mathbrown}{d}}\color{mathbrown}{\:}\mathrm{\color{mathbrown}{c}\color{mathbrown}{i}\color{mathbrown}{r}\color{mathbrown}{c}\color{mathbrown}{l}\color{mathbrown}{e}}\color{mathbrown}{\:} \\ $$ $$\mathrm{Midpoint}\:\mathrm{of}\:\begin{cases}{\mathrm{P}_{\mathrm{1}} \left(\mathrm{0},\mathrm{1}\right)}\\{\mathrm{P}_{\mathrm{2}} \left(\mathrm{1},\mathrm{4}\right)}\end{cases}\:\mathrm{is}\:\mathrm{S}\left(\frac{\mathrm{1}}{\mathrm{2}},\frac{\mathrm{5}}{\mathrm{2}}\right) \\ $$ $$\mathrm{and}\:\mathrm{the}\:\mathrm{slope}\:\mathrm{is}\:\mathrm{m}\:=\:\frac{\mathrm{4}−\mathrm{1}}{\mathrm{1}−\mathrm{0}}\:=\:\mathrm{3},\:\mathrm{the}\:\mathrm{perpendicular} \\ $$ $$\mathrm{slope}\:\mathrm{is}\:{m}_{{p}} \:=−\frac{\mathrm{1}}{\mathrm{3}}.\:\mathrm{\color{mathred}{t}\color{mathred}{h}\color{mathred}{e}}\color{mathred}{\:}\mathrm{\color{mathred}{l}\color{mathred}{i}\color{mathred}{n}\color{mathred}{e}}\color{mathred}{\:}\mathrm{\color{mathred}{e}\color{mathred}{q}\color{mathred}{u}\color{mathred}{a}\color{mathred}{t}\color{mathred}{i}\color{mathred}{o}\color{mathred}{n}}\color{mathred}{\:} \\ $$ $$\color{mathred}{\Rightarrow}\mathrm{\color{mathred}{y}}\color{mathred}{=}\color{mathred}{−}\frac{\mathrm{\color{mathred}{1}}}{\mathrm{\color{mathred}{3}}}\color{mathred}{\left(}\mathrm{\color{mathred}{x}}\color{mathred}{−}\frac{\mathrm{\color{mathred}{1}}}{\mathrm{\color{mathred}{2}}}\color{mathred}{\right)}\color{mathred}{+}\frac{\mathrm{\color{mathred}{5}}}{\mathrm{\color{mathred}{2}}} \\ $$ $$\color{mathred}{\Rightarrow}\mathrm{\color{mathred}{y}}\color{mathred}{=}\color{mathred}{−}\frac{\mathrm{\color{mathred}{1}}}{\mathrm{\color{mathred}{3}}}\mathrm{\color{mathred}{x}}\color{mathred}{+}\frac{\mathrm{\color{mathred}{8}}}{\mathrm{\color{mathred}{3}}} \\ $$ $$\mathrm{\color{mathblue}{M}\color{mathblue}{i}\color{mathblue}{d}\color{mathblue}{p}\color{mathblue}{o}\color{mathblue}{i}\color{mathblue}{n}\color{mathblue}{t}}\color{mathblue}{\:}\mathrm{\color{mathblue}{o}\color{mathblue}{f}}\color{mathblue}{\:}\begin{cases}{\mathrm{\color{mathblue}{P}}_{\mathrm{\color{mathblue}{2}}} \color{mathblue}{\left(}\mathrm{\color{mathblue}{1}}\color{mathblue}{,}\mathrm{\color{mathblue}{4}}\color{mathblue}{\right)}}\\{\mathrm{\color{mathblue}{P}}_{\mathrm{\color{mathblue}{3}}} \color{mathblue}{\left(}\mathrm{\color{mathblue}{5}}\color{mathblue}{,}\mathrm{\color{mathblue}{2}}\color{mathblue}{\right)}}\end{cases}\mathrm{\color{mathblue}{i}\color{mathblue}{s}}\color{mathblue}{\:}\mathrm{\color{mathblue}{Q}}\color{mathblue}{\left(}\mathrm{\color{mathblue}{3}}\color{mathblue}{,}\mathrm{\color{mathblue}{3}}\color{mathblue}{\right)} \\ $$ $$\mathrm{\color{mathblue}{a}\color{mathblue}{n}\color{mathblue}{d}}\color{mathblue}{\:}\mathrm{\color{mathblue}{t}\color{mathblue}{h}\color{mathblue}{e}}\color{mathblue}{\:}\mathrm{\color{mathblue}{s}\color{mathblue}{l}\color{mathblue}{o}\color{mathblue}{p}\color{mathblue}{e}}\color{mathblue}{\:}\mathrm{\color{mathblue}{i}\color{mathblue}{s}}\color{mathblue}{\:}\mathrm{\color{mathblue}{m}}_{\mathrm{\color{mathblue}{2}}} \color{mathblue}{=}\frac{\mathrm{\color{mathblue}{4}}\color{mathblue}{−}\mathrm{\color{mathblue}{2}}}{\mathrm{\color{mathblue}{1}}\color{mathblue}{−}\mathrm{\color{mathblue}{5}}}\color{mathblue}{=}\color{mathblue}{−}\frac{\mathrm{\color{mathblue}{1}}}{\mathrm{\color{mathblue}{2}}}\color{mathblue}{,}\mathrm{\color{mathblue}{t}\color{mathblue}{h}\color{mathblue}{e}}\color{mathblue}{\:}\mathrm{\color{mathblue}{p}\color{mathblue}{e}\color{mathblue}{r}\color{mathblue}{p}\color{mathblue}{e}\color{mathblue}{n}\color{mathblue}{d}\color{mathblue}{i}\color{mathblue}{c}\color{mathblue}{u}\color{mathblue}{l}\color{mathblue}{a}\color{mathblue}{r}} \\ $$ $$\mathrm{\color{mathblue}{s}\color{mathblue}{l}\color{mathblue}{o}\color{mathblue}{p}\color{mathblue}{e}}\color{mathblue}{\:}\mathrm{\color{mathblue}{i}\color{mathblue}{s}}\color{mathblue}{\:}{\color{mathblue}{m}}_{{\color{mathblue}{p}}_{\mathrm{\color{mathblue}{2}}} } \color{mathblue}{=}\color{mathblue}{\:}\mathrm{\color{mathblue}{2}}\color{mathblue}{\:}\color{mathblue}{,}\color{mathblue}{\:}\mathrm{the}\:\mathrm{line}\:\mathrm{equation}\: \\ $$ $$\Rightarrow\mathrm{y}=\mathrm{2}\left(\mathrm{x}−\mathrm{3}\right)+\mathrm{3}\:;\:\mathrm{y}\:=\:\mathrm{2x}−\mathrm{3} \\ $$ $$\mathrm{set}\:\mathrm{the}\:\mathrm{two}\:\mathrm{equation}\:\mathrm{to}\:\mathrm{find}\:\mathrm{x}\:\mathrm{and}\:\mathrm{y},\:\mathrm{after} \\ $$ $$\mathrm{solving}\:\mathrm{we}\:\mathrm{get}\:\begin{cases}{\mathrm{x}=\:\frac{\mathrm{17}}{\mathrm{7}}}\\{\mathrm{y}=\frac{\mathrm{13}}{\mathrm{7}}}\end{cases}\:,\:\mathrm{so}\:\mathrm{the}\:\mathrm{center} \\ $$ $$\mathrm{point}\:\mathrm{is}\:\left(\frac{\mathrm{17}}{\mathrm{7}},\frac{\mathrm{13}}{\mathrm{7}}\right)\:\mathrm{with}\:\mathrm{radius}\:=\sqrt{\left(\mathrm{0}−\frac{\mathrm{17}}{\mathrm{7}}\right)^{\mathrm{2}} +\left(\mathrm{1}−\frac{\mathrm{13}}{\mathrm{7}}\right)^{\mathrm{2}} } \\ $$ $$\mathrm{r}\:=\sqrt{\frac{\mathrm{289}+\mathrm{36}}{\mathrm{49}}}\:=\:\sqrt{\frac{\mathrm{325}}{\mathrm{49}}} \\ $$ $$\mathrm{\color{mathred}{T}\color{mathred}{h}\color{mathred}{e}\color{mathred}{r}\color{mathred}{e}\color{mathred}{f}\color{mathred}{o}\color{mathred}{r}\color{mathred}{e}}\color{mathred}{\:}\mathrm{\color{mathred}{t}\color{mathred}{h}\color{mathred}{e}}\color{mathred}{\:}\mathrm{\color{mathred}{c}\color{mathred}{i}\color{mathred}{r}\color{mathred}{c}\color{mathred}{l}\color{mathred}{e}}\color{mathred}{'}\mathrm{\color{mathred}{s}}\color{mathred}{\:}\mathrm{\color{mathred}{e}\color{mathred}{q}\color{mathred}{u}\color{mathred}{a}\color{mathred}{t}\color{mathred}{i}\color{mathred}{o}\color{mathred}{n}}\color{mathred}{\:}\mathrm{\color{mathred}{i}\color{mathred}{s}}\color{mathred}{\:} \\ $$ $$\underline{\color{mathred}{\left(}\mathrm{\color{mathred}{x}}\color{mathred}{−}\frac{\mathrm{\color{mathred}{1}\color{mathred}{7}}}{\mathrm{\color{mathred}{7}}}\color{mathred}{\right)}^{\mathrm{\color{mathred}{2}}} \color{mathred}{+}\color{mathred}{\left(}\mathrm{\color{mathred}{y}}\color{mathred}{−}\frac{\mathrm{\color{mathred}{1}\color{mathred}{3}}}{\mathrm{\color{mathred}{7}}}\color{mathred}{\right)}^{\mathrm{\color{mathred}{2}}} \color{mathred}{=}\color{mathred}{\:}\frac{\mathrm{\color{mathred}{3}\color{mathred}{2}\color{mathred}{5}}}{\mathrm{\color{mathred}{4}\color{mathred}{9}}}}\color{mathred}{\:} \\ $$ $$ \\ $$

Commented bybramlexs22 last updated on 07/Mar/21

Commented bybramlexs22 last updated on 07/Mar/21

nice....

$$\mathrm{nice}.... \\ $$

Commented bygreg_ed last updated on 07/Mar/21

well done, sir EDWIN88 !

$$\boldsymbol{\mathrm{well}}\:\boldsymbol{\mathrm{done}},\:\boldsymbol{\mathrm{sir}}\:\boldsymbol{\mathrm{EDWIN}}\mathrm{88}\:! \\ $$

Answered by john_santu last updated on 07/Mar/21

Let C(x,y) be a center point the circle we get the equation (i) (√(x^2 +(y−1)^2 )) = (√((x−1)^2 +(y−4)^2 )) (ii)(√(x^2 +(y−1)^2 )) =(√((x−5)^2 +(y−2)^2 )) (i)→x^2 +y^2 −2y+1=x^2 −2x+1+y^2 −8y+16 ⇒2x+6y=16 ; x+3y=8 (ii)→x^2 +y^2 −2y+1=x^2 −10x+25+y^2 −4y+4 ⇒10x+2y=28 ; 5x+y=14 solve for two equation ⇒x+3(14−5x)= 8 ⇒42−14x = 8 ; x=((34)/(14)) = ((17)/7) and y = 14−((85)/7) = ((13)/7) then we find radius =(√((((17)/7)−0)^2 +(((13)/7)−1)^2 )) radius =(√((289+36)/(49))) = (√((325)/(49))) ∴ (x−((17)/7))^2 +(y−((13)/7))^2 =((325)/(49))

$${Let}\:{C}\left({x},{y}\right)\:{be}\:{a}\:{center}\:{point}\:{the}\:{circle} \\ $$ $${we}\:{get}\:{the}\:{equation}\: \\ $$ $$\color{mathblue}{\left(}{\color{mathblue}{i}}\color{mathblue}{\right)}\color{mathblue}{\:}\sqrt{{\color{mathblue}{x}}^{\mathrm{\color{mathblue}{2}}} \color{mathblue}{+}\color{mathblue}{\left(}{\color{mathblue}{y}}\color{mathblue}{−}\mathrm{\color{mathblue}{1}}\color{mathblue}{\right)}^{\mathrm{\color{mathblue}{2}}} }\color{mathblue}{\:}\color{mathblue}{=}\color{mathblue}{\:}\sqrt{\color{mathblue}{\left(}{\color{mathblue}{x}}\color{mathblue}{−}\mathrm{\color{mathblue}{1}}\color{mathblue}{\right)}^{\mathrm{\color{mathblue}{2}}} \color{mathblue}{+}\color{mathblue}{\left(}{\color{mathblue}{y}}\color{mathblue}{−}\mathrm{\color{mathblue}{4}}\color{mathblue}{\right)}^{\mathrm{\color{mathblue}{2}}} } \\ $$ $$\color{mathbrown}{\left(}{\color{mathbrown}{i}\color{mathbrown}{i}}\color{mathbrown}{\right)}\sqrt{{\color{mathbrown}{x}}^{\mathrm{\color{mathbrown}{2}}} \color{mathbrown}{+}\color{mathbrown}{\left(}{\color{mathbrown}{y}}\color{mathbrown}{−}\mathrm{\color{mathbrown}{1}}\color{mathbrown}{\right)}^{\mathrm{\color{mathbrown}{2}}} }\color{mathbrown}{\:}\color{mathbrown}{=}\sqrt{\color{mathbrown}{\left(}{\color{mathbrown}{x}}\color{mathbrown}{−}\mathrm{\color{mathbrown}{5}}\color{mathbrown}{\right)}^{\mathrm{\color{mathbrown}{2}}} \color{mathbrown}{+}\color{mathbrown}{\left(}{\color{mathbrown}{y}}\color{mathbrown}{−}\mathrm{\color{mathbrown}{2}}\color{mathbrown}{\right)}^{\mathrm{\color{mathbrown}{2}}} } \\ $$ $$\color{mathblue}{\left(}{\color{mathblue}{i}}\color{mathblue}{\right)}\color{mathblue}{\rightarrow}{\color{mathblue}{x}}^{\mathrm{\color{mathblue}{2}}} \color{mathblue}{+}{\color{mathblue}{y}}^{\mathrm{\color{mathblue}{2}}} \color{mathblue}{−}\mathrm{\color{mathblue}{2}}{\color{mathblue}{y}}\color{mathblue}{+}\mathrm{\color{mathblue}{1}}\color{mathblue}{=}{\color{mathblue}{x}}^{\mathrm{\color{mathblue}{2}}} \color{mathblue}{−}\mathrm{\color{mathblue}{2}}{\color{mathblue}{x}}\color{mathblue}{+}\mathrm{\color{mathblue}{1}}\color{mathblue}{+}{\color{mathblue}{y}}^{\mathrm{\color{mathblue}{2}}} \color{mathblue}{−}\mathrm{\color{mathblue}{8}}{\color{mathblue}{y}}\color{mathblue}{+}\mathrm{\color{mathblue}{1}\color{mathblue}{6}} \\ $$ $$\color{mathblue}{\Rightarrow}\mathrm{\color{mathblue}{2}}{\color{mathblue}{x}}\color{mathblue}{+}\mathrm{\color{mathblue}{6}}{\color{mathblue}{y}}\color{mathblue}{=}\mathrm{\color{mathblue}{1}\color{mathblue}{6}}\color{mathblue}{\:}\color{mathblue}{;}\color{mathblue}{\:}{\color{mathblue}{x}}\color{mathblue}{+}\mathrm{\color{mathblue}{3}}{\color{mathblue}{y}}\color{mathblue}{=}\mathrm{\color{mathblue}{8}}\color{mathblue}{\:} \\ $$ $$\color{mathbrown}{\left(}{\color{mathbrown}{i}\color{mathbrown}{i}}\color{mathbrown}{\right)}\color{mathbrown}{\rightarrow}{\color{mathbrown}{x}}^{\mathrm{\color{mathbrown}{2}}} \color{mathbrown}{+}{\color{mathbrown}{y}}^{\mathrm{\color{mathbrown}{2}}} \color{mathbrown}{−}\mathrm{\color{mathbrown}{2}}{\color{mathbrown}{y}}\color{mathbrown}{+}\mathrm{\color{mathbrown}{1}}\color{mathbrown}{=}{\color{mathbrown}{x}}^{\mathrm{\color{mathbrown}{2}}} \color{mathbrown}{−}\mathrm{\color{mathbrown}{1}\color{mathbrown}{0}}{\color{mathbrown}{x}}\color{mathbrown}{+}\mathrm{\color{mathbrown}{2}\color{mathbrown}{5}}\color{mathbrown}{+}{\color{mathbrown}{y}}^{\mathrm{\color{mathbrown}{2}}} \color{mathbrown}{−}\mathrm{\color{mathbrown}{4}}{\color{mathbrown}{y}}\color{mathbrown}{+}\mathrm{\color{mathbrown}{4}} \\ $$ $$\color{mathbrown}{\Rightarrow}\mathrm{\color{mathbrown}{1}\color{mathbrown}{0}}{\color{mathbrown}{x}}\color{mathbrown}{+}\mathrm{\color{mathbrown}{2}}{\color{mathbrown}{y}}\color{mathbrown}{=}\mathrm{\color{mathbrown}{2}\color{mathbrown}{8}}\color{mathbrown}{\:}\color{mathbrown}{;}\color{mathbrown}{\:}\mathrm{\color{mathbrown}{5}}{\color{mathbrown}{x}}\color{mathbrown}{+}{\color{mathbrown}{y}}\color{mathbrown}{=}\mathrm{\color{mathbrown}{1}\color{mathbrown}{4}} \\ $$ $${solve}\:{for}\:{two}\:{equation}\: \\ $$ $$\color{mathred}{\Rightarrow}{\color{mathred}{x}}\color{mathred}{+}\mathrm{\color{mathred}{3}}\color{mathred}{\left(}\mathrm{\color{mathred}{1}\color{mathred}{4}}\color{mathred}{−}\mathrm{\color{mathred}{5}}{\color{mathred}{x}}\color{mathred}{\right)}\color{mathred}{=}\color{mathred}{\:}\mathrm{\color{mathred}{8}} \\ $$ $$\color{mathred}{\Rightarrow}\mathrm{\color{mathred}{4}\color{mathred}{2}}\color{mathred}{−}\mathrm{\color{mathred}{1}\color{mathred}{4}}{\color{mathred}{x}}\color{mathred}{\:}\color{mathred}{=}\color{mathred}{\:}\mathrm{\color{mathred}{8}}\color{mathred}{\:}\color{mathred}{;}\color{mathred}{\:}{\color{mathred}{x}}\color{mathred}{=}\frac{\mathrm{\color{mathred}{3}\color{mathred}{4}}}{\mathrm{\color{mathred}{1}\color{mathred}{4}}}\color{mathred}{\:}\color{mathred}{=}\color{mathred}{\:}\frac{\mathrm{\color{mathred}{1}\color{mathred}{7}}}{\mathrm{\color{mathred}{7}}} \\ $$ $${\color{mathred}{a}\color{mathred}{n}\color{mathred}{d}}\color{mathred}{\:}{\color{mathred}{y}}\color{mathred}{\:}\color{mathred}{=}\color{mathred}{\:}\mathrm{\color{mathred}{1}\color{mathred}{4}}\color{mathred}{−}\frac{\mathrm{\color{mathred}{8}\color{mathred}{5}}}{\mathrm{\color{mathred}{7}}}\color{mathred}{\:}\color{mathred}{=}\color{mathred}{\:}\frac{\mathrm{\color{mathred}{1}\color{mathred}{3}}}{\mathrm{\color{mathred}{7}}} \\ $$ $${then}\:{we}\:{find}\:{radius}\:=\sqrt{\left(\frac{\mathrm{17}}{\mathrm{7}}−\mathrm{0}\right)^{\mathrm{2}} +\left(\frac{\mathrm{13}}{\mathrm{7}}−\mathrm{1}\right)^{\mathrm{2}} } \\ $$ $${radius}\:=\sqrt{\frac{\mathrm{289}+\mathrm{36}}{\mathrm{49}}}\:=\:\sqrt{\frac{\mathrm{325}}{\mathrm{49}}} \\ $$ $$\color{mathred}{\therefore}\color{mathred}{\:}\color{mathred}{\left(}{\color{mathred}{x}}\color{mathred}{−}\frac{\mathrm{\color{mathred}{1}\color{mathred}{7}}}{\mathrm{\color{mathred}{7}}}\color{mathred}{\right)}^{\mathrm{\color{mathred}{2}}} \color{mathred}{+}\color{mathred}{\left(}{\color{mathred}{y}}\color{mathred}{−}\frac{\mathrm{\color{mathred}{1}\color{mathred}{3}}}{\mathrm{\color{mathred}{7}}}\color{mathred}{\right)}^{\mathrm{\color{mathred}{2}}} \color{mathred}{=}\frac{\mathrm{\color{mathred}{3}\color{mathred}{2}\color{mathred}{5}}}{\mathrm{\color{mathred}{4}\color{mathred}{9}}} \\ $$

Answered by mr W last updated on 07/Mar/21

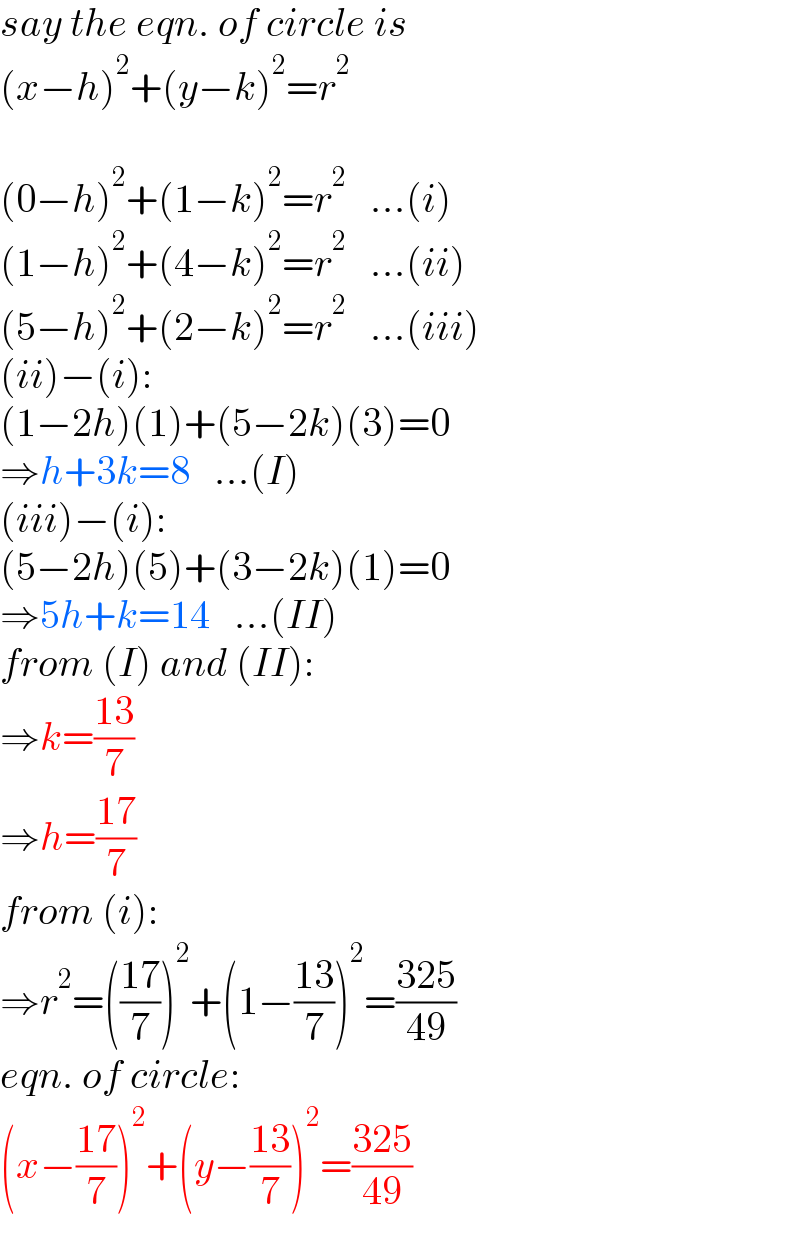
say the eqn. of circle is (x−h)^2 +(y−k)^2 =r^2 (0−h)^2 +(1−k)^2 =r^2 ...(i) (1−h)^2 +(4−k)^2 =r^2 ...(ii) (5−h)^2 +(2−k)^2 =r^2 ...(iii) (ii)−(i): (1−2h)(1)+(5−2k)(3)=0 ⇒h+3k=8 ...(I) (iii)−(i): (5−2h)(5)+(3−2k)(1)=0 ⇒5h+k=14 ...(II) from (I) and (II): ⇒k=((13)/7) ⇒h=((17)/7) from (i): ⇒r^2 =(((17)/7))^2 +(1−((13)/7))^2 =((325)/(49)) eqn. of circle: (x−((17)/7))^2 +(y−((13)/7))^2 =((325)/(49))

$${say}\:{the}\:{eqn}.\:{of}\:{circle}\:{is} \\ $$ $$\left({x}−{h}\right)^{\mathrm{2}} +\left({y}−{k}\right)^{\mathrm{2}} ={r}^{\mathrm{2}} \\ $$ $$ \\ $$ $$\left(\mathrm{0}−{h}\right)^{\mathrm{2}} +\left(\mathrm{1}−{k}\right)^{\mathrm{2}} ={r}^{\mathrm{2}} \:\:\:...\left({i}\right) \\ $$ $$\left(\mathrm{1}−{h}\right)^{\mathrm{2}} +\left(\mathrm{4}−{k}\right)^{\mathrm{2}} ={r}^{\mathrm{2}} \:\:\:...\left({ii}\right) \\ $$ $$\left(\mathrm{5}−{h}\right)^{\mathrm{2}} +\left(\mathrm{2}−{k}\right)^{\mathrm{2}} ={r}^{\mathrm{2}} \:\:\:...\left({iii}\right) \\ $$ $$\left({ii}\right)−\left({i}\right): \\ $$ $$\left(\mathrm{1}−\mathrm{2}{h}\right)\left(\mathrm{1}\right)+\left(\mathrm{5}−\mathrm{2}{k}\right)\left(\mathrm{3}\right)=\mathrm{0} \\ $$ $$\Rightarrow{\color{mathblue}{h}}\color{mathblue}{+}\mathrm{\color{mathblue}{3}}{\color{mathblue}{k}}\color{mathblue}{=}\mathrm{\color{mathblue}{8}}\:\:\:...\left({I}\right) \\ $$ $$\left({iii}\right)−\left({i}\right): \\ $$ $$\left(\mathrm{5}−\mathrm{2}{h}\right)\left(\mathrm{5}\right)+\left(\mathrm{3}−\mathrm{2}{k}\right)\left(\mathrm{1}\right)=\mathrm{0} \\ $$ $$\Rightarrow\mathrm{\color{mathblue}{5}}{\color{mathblue}{h}}\color{mathblue}{+}{\color{mathblue}{k}}\color{mathblue}{=}\mathrm{\color{mathblue}{1}\color{mathblue}{4}}\:\:\:...\left({II}\right) \\ $$ $${from}\:\left({I}\right)\:{and}\:\left({II}\right): \\ $$ $$\Rightarrow{\color{mathred}{k}}\color{mathred}{=}\frac{\mathrm{\color{mathred}{1}\color{mathred}{3}}}{\mathrm{\color{mathred}{7}}} \\ $$ $$\Rightarrow{\color{mathred}{h}}\color{mathred}{=}\frac{\mathrm{\color{mathred}{1}\color{mathred}{7}}}{\mathrm{\color{mathred}{7}}} \\ $$ $${from}\:\left({i}\right): \\ $$ $$\Rightarrow{r}^{\mathrm{2}} =\left(\frac{\mathrm{17}}{\mathrm{7}}\right)^{\mathrm{2}} +\left(\mathrm{1}−\frac{\mathrm{13}}{\mathrm{7}}\right)^{\mathrm{2}} =\frac{\mathrm{325}}{\mathrm{49}} \\ $$ $${eqn}.\:{of}\:{circle}: \\ $$ $$\color{mathred}{\left(}{\color{mathred}{x}}\color{mathred}{−}\frac{\mathrm{\color{mathred}{1}\color{mathred}{7}}}{\mathrm{\color{mathred}{7}}}\color{mathred}{\right)}^{\mathrm{\color{mathred}{2}}} \color{mathred}{+}\color{mathred}{\left(}{\color{mathred}{y}}\color{mathred}{−}\frac{\mathrm{\color{mathred}{1}\color{mathred}{3}}}{\mathrm{\color{mathred}{7}}}\color{mathred}{\right)}^{\mathrm{\color{mathred}{2}}} \color{mathred}{=}\frac{\mathrm{\color{mathred}{3}\color{mathred}{2}\color{mathred}{5}}}{\mathrm{\color{mathred}{4}\color{mathred}{9}}} \\ $$

Commented bymr W last updated on 07/Mar/21

Commented bybramlexs22 last updated on 07/Mar/21

how do you sir make a point in your graph?

$$\mathrm{how}\:\mathrm{do}\:\mathrm{you}\:\mathrm{sir}\:\mathrm{make}\:\mathrm{a}\:\mathrm{point}\:\mathrm{in}\:\mathrm{your} \\ $$ $$\mathrm{graph}? \\ $$

Commented bymr W last updated on 07/Mar/21

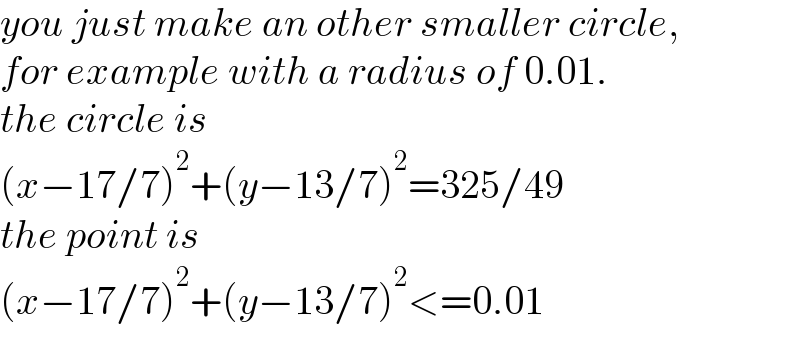
you just make an other smaller circle, for example with a radius of 0.01. the circle is (x−17/7)^2 +(y−13/7)^2 =325/49 the point is (x−17/7)^2 +(y−13/7)^2 <=0.01

$${you}\:{just}\:{make}\:{an}\:{other}\:{smaller}\:{circle},\: \\ $$ $${for}\:{example}\:{with}\:{a}\:{radius}\:{of}\:\mathrm{0}.\mathrm{01}. \\ $$ $${the}\:{circle}\:{is} \\ $$ $$\left({x}−\mathrm{17}/\mathrm{7}\right)^{\mathrm{2}} +\left({y}−\mathrm{13}/\mathrm{7}\right)^{\mathrm{2}} =\mathrm{325}/\mathrm{49} \\ $$ $${the}\:{point}\:{is} \\ $$ $$\left({x}−\mathrm{17}/\mathrm{7}\right)^{\mathrm{2}} +\left({y}−\mathrm{13}/\mathrm{7}\right)^{\mathrm{2}} <=\mathrm{0}.\mathrm{01} \\ $$

Commented bymr W last updated on 07/Mar/21

Commented bybramlexs22 last updated on 07/Mar/21

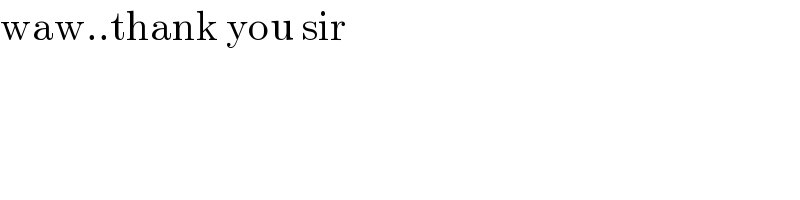
waw..thank you sir

$$\mathrm{waw}..\mathrm{thank}\:\mathrm{you}\:\mathrm{sir} \\ $$

Commented bygreg_ed last updated on 01/Apr/21

very nice !

$$\boldsymbol{\mathrm{\color{mathblue}{v}\color{mathblue}{e}\color{mathblue}{r}\color{mathblue}{y}}}\color{mathblue}{\:}\boldsymbol{\mathrm{\color{mathblue}{n}\color{mathblue}{i}\color{mathblue}{c}\color{mathblue}{e}}}\color{mathblue}{\:}\color{mathblue}{!} \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com