Math Question and Answers


Question and Answers Forum

All Question Topic List
Question Number 134817 by bramlexs22 last updated on 07/Mar/21

What is the maximum value of abc if a+b+c = 5 and ab+bc+ca = 7?\n
Commented bybramlexs22 last updated on 09/Mar/21

$thanks you all sir$
Commented byjohn_santu last updated on 08/Mar/21
$let a+b = x then c = 5−x (i) xc = (a+b)c = ac+bc = 7−ab then ab = 7−xc so abc = (7−xc)c abc = 7c−xc^2 , injecting c=5−x we get abc = f(x)= 7(5−x)−x(5−x)^2 f(x)= 35−7x−x(x^2 −10x+25) f(x)=−x^3 +10x^2 −32x+35 (df/dx) = −3x^2 +20x−32 = 0 we get { ((x=(8/3))),((x=4)) :} (d^2 f/dx^2 ) = −6x+20∣_(x= 4) <0 and (d^2 f/dx^2 ) = −6x+20∣_(x = (8/3)) = −((48)/3)+20 >0 so f(x)_(max) for x = 4 and f(x)_(min ) for x=(8/3) ∴ max value is f(4)=−4^3 +10.4^2 −32.4+35 f(4)= −64+160−128+35 = 3 when a+b=4 and c = 1 . from eq(2) ab+ac+bc = 7⇒ab+a+b = 7 ; ab = 3 ∧b = 4−a ; we get a(4−a)=3 a^2 −4a+3 = 0 → { ((a=1→b=3 or)),((a=3→b=1 )) :} (a,b,c) = (1,3,1) or (3,1,1) clearly max is f(4) = 3 min value is f((8/3))=−((8/3))^3 +10((8/3))^2 −32((8/3))+35$
$l e t a + b = x t h e n c = 5 - x$ $(i) x c = (a + b) c = a c + b c = 7 - a b$ $t h e n a b = 7 - x c s o a b c = (7 - x c) c$ $a b c = 7 c - {x c}^{2}, i n j e c t i n g c = 5 - x$ $Extra close brace or missing open brace$ $Extra close brace or missing open brace$ $Extra close brace or missing open brace$ $\frac{d f}{d x} = - 3 x^{2} + 20 x - 32 = 0$ $w e g e t {\begin{cases} x = \frac{8}{3} \\ x = 4 \end{cases}$ $\frac{d^{2} f}{{d x}^{2}} = - 6 x + 20 ∣_{x = 4} < 0 a n d$ $\frac{d^{2} f}{{d x}^{2}} = - 6 x + 20 ∣_{x = \frac{8}{3}} = - \frac{48}{3} + 20 > 0$ $Extra close brace or missing open brace$ $Extra close brace or missing open brace$ $Extra close brace or missing open brace$ $w h e n a + b = 4 a n d c = 1 . f r o m e q (2)$ $a b + a c + b c = 7 \Rightarrow a b + a + b = 7;$ $a b = 3 \land b = 4 - a; w e g e t a (4 - a) = 3$ $a^{2} - 4 a + 3 = 0 \to {\begin{cases} a = 1 \to b = 3 o r \\ a = 3 \to b = 1 \end{cases}$ $(a, b, c) = (1, 3, 1) o r (3, 1, 1)$ $c l e a r l y m a x i s f (4) = 3$ $m i n v a l u e i s f (\frac{8}{3}) = - {(\frac{8}{3})}^{3} + 10 {(\frac{8}{3})}^{2} - 32 (\frac{8}{3}) + 35$
Commented bymr W last updated on 08/Mar/21

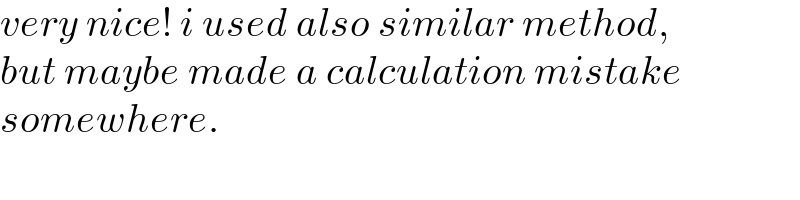
$v e r y n i c e! i u s e d a l s o s i m i l a r m e t h o d,$ $b u t m a y b e m a d e a c a l c u l a t i o n m i s t a k e$ $s o m e w h e r e .$
	Answered by liberty last updated on 07/Mar/21
	$(1)a=5−(b+c) (2) (5−(b+c))b+bc+c(5−(b+c))=7 ⇒ 5b−b^2 −bc+bc+5c−bc−c^2 =7 ⇒5b−b^2 −bc+5c+c^2 = 7 (3)abc = (5−(b+c))bc =5bc−b^2 c−bc^2 let f(b,c)=5bc−b^2 c−bc^2 +λ(5b−b^2 −bc+5c+c^2 −7) (i) f_b = 5c−2bc−c^2 +λ(5−2b−c)=0 (ii)f_c = 5b−b^2 −2bc+λ(−b+5+2c)= 0 (iii)f_(λ ) = 5b−b^2 −bc+5c+c^2 = 7 from eq (i) &(ii) we get { ((λ=((c^2 +2bc−5c)/(5−2b−c)))),((λ = ((b^2 +2bc−5b)/(5−b+2c)))) :} and b^2 −5b = c^2 +5c−bc−7 ⇒ λ = λ ; ((c^2 +2bc−5c)/(5−2b−c)) = ((c^2 +5c−bc−7+2bc)/(5−b+2c)) next...$
	$(1) a = 5 - (b + c) (2) (5 - (b + c)) b + b c + c (5 - (b + c)) = 7$ $\Rightarrow 5 b - b^{2} - b c + b c + 5 c - b c - c^{2} = 7$ $\Rightarrow 5 b - b^{2} - b c + 5 c + c^{2} = 7$ $(3) a b c = (5 - (b + c)) b c = 5 b c - b^{2} c - {b c}^{2}$ $l e t f (b, c) = 5 b c - b^{2} c - {b c}^{2} + λ (5 b - b^{2} - b c + 5 c + c^{2} - 7)$ $Extra close brace or missing open brace$ $Extra close brace or missing open brace$ $Extra close brace or missing open brace$ $Extra close brace or missing open brace$ $a n d b^{2} - 5 b = c^{2} + 5 c - b c - 7$ $\Rightarrow λ = λ; \frac{c^{2} + 2 b c - 5 c}{5 - 2 b - c} = \frac{c^{2} + 5 c - b c - 7 + 2 b c}{5 - b + 2 c}$ $n e x t . . .$
	Answered by mr W last updated on 08/Mar/21

	$c = 5 - (a + b)$ $a b + (a + b) c = 7$ $c = \frac{7 - a b}{a + b} = 5 - (a + b)$ $\Rightarrow a b = 7 - (a + b) (5 - (a + b))$ $P = a b c = a b (5 - (a + b)) = [7 - (a + b) (5 - (a + b))] (5 - (a + b))$ $l e t t = a + b$ $\Rightarrow P = [7 - t (5 - t)] (5 - t) = - t^{3} + 10 t^{2} - 32 t + 35$ $\frac{d P}{d t} = - 3 t^{2} + 20 t - 32 = 0$ $(3 t - 8) (t - 4) = 0$ $\Rightarrow t = \frac{8}{3}, 4$ $\frac{d^{2} P}{{d t}^{2}} = - 6 t + 20$ $a t t = \frac{8}{3} : \frac{d^{2} P}{{d t}^{2}} = - 6 \times \frac{8}{3} + 20 = 4 > 0 \Rightarrow m i n .$ $a t t = 4 : \frac{d^{2} P}{{d t}^{2}} = - 6 \times 4 + 20 = - 4 < 0 \Rightarrow m a x .$ $\Rightarrow P_{m i n} = [7 - \frac{8}{3} (5 - \frac{8}{3})] (5 - \frac{8}{3}) = \frac{49}{27}$ $\Rightarrow P_{m a x} = [7 - 4 (5 - 4)] (5 - 4) = 3$
	Answered by ajfour last updated on 08/Mar/21

	$x^{3} - 5 x^{2} + 7 x - m = 0$ $w h e r e$ $a + b + c = 5$ $a b + b c + c a = 7$ $a b c = m$ $m = x^{3} - 5 x^{2} + 7 x$ $\frac{d m}{d x} = 3 x^{2} - 10 x + 7$ $x = \frac{10 \pm \sqrt{100 - 84}}{6}$ $x = \frac{10 \pm 4}{6} \Rightarrow x = 1, \frac{7}{3}$ $f o r x = 1, m = 3$ $f o r x = \frac{7}{3}, m = \frac{49}{27}$ $h e n c e {(a b c)}_{m a x} = m_{m a x} = 3$
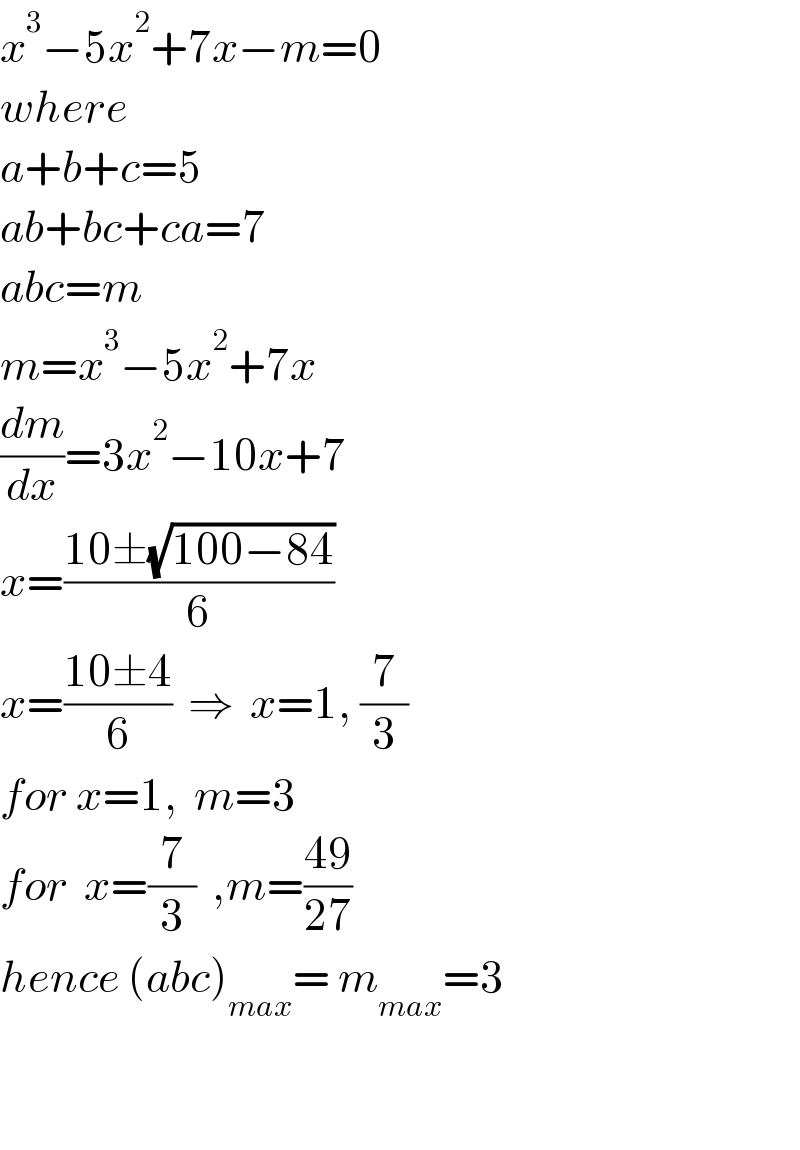
	Commented bymr W last updated on 09/Mar/21

	$n i c e i d e a!$
	Commented byajfour last updated on 09/Mar/21

	$t h a n k s s i r, m l i t t l e s h a k e n b y$ $c i r c u m s t a n c e s, n a n y w a y t a k e n$ $t o w a t c h i n g U t u b e m o v i e s n$ $m u s i c, c a n t f o c u s h e r e l i k e i$ $u s e d t o, l e t s s e e h o w l o n g; I m$ $s o v e r y u n p r e d i c t a b l e e v e n t o$ $m y s e l f . . .$
	Commented bymr W last updated on 09/Mar/21

	$t a k e b e s t c a r e o f y o u r s e l f s i r!$
Terms of Service
Privacy Policy
Contact: info@tinkutara.com

Question and Answers Forum