Math Question and Answers


Question and Answers Forum

All Question Topic List
Question Number 135004 by bramlexs22 last updated on 09/Mar/21

the closest distance from the point on the curve y = x ^ 3-1 to the curve x = y ^2+ 4 is equal to\n
Commented bybramlexs22 last updated on 09/Mar/21

Commented byEDWIN88 last updated on 09/Mar/21
$step(1) slope of tangent line curve y=x^3 −1 at point P(a,a^3 −1) is m_1 =3a^2 then slope of normal line is −(1/(3a^2 )) the equation of normal line at point (a,a^3 −1) is y=−(1/(3a^2 ))(x−a)+a^3 −1⇒y =−(x/(3a^2 ))+(1/(3a))+a^3 −1 step(2) slope of tangent line curve y^2 =x−4 at point Q(b^2 +4, b) is m_2 = (1/(2b)) , then slope of normal line is −2b , and the equation of normal line equal to y = −2b(x−b^2 −4)+b⇒y=−2bx+2b^3 +9b step(3) the both of equation of normal line is same , we get { ((−(1/(3a^2 )) = −2b ; a^2 b = (1/6))),(((1/(3a))+a^3 −1 = 2b^3 +9b)) :} solving for a and b , ⇒(1/(3a))+a^3 −1=2((1/(6a^2 )))^3 +9((1/(6a^2 ))) ⇒(1/(3a))+a^3 −1 = (1/(108a^6 )) +(3/(2a^2 )) 36a^5 +108a^9 −108a^6 =1+162a^4 108a^9 −108a^6 +36a^5 −162a^4 −1=0 we get { ((a=1.2067)),((b = 0.1145)) :} we get a point P(1.2067; 0.7571) and Q(4.0131; 0.1145) therefore the closest distance is ∣PQ∣ = (√((4.0131−1.2067)^2 +(0.1145−0.7571)^2 )) ∣PQ∣ ≈ 2.87903$
$step (1) slope of tangent line curve y = x^{3} - 1 at point P (a, a^{3} - 1)$ $is m_{1} = {3 a}^{2} then slope of normal line is - \frac{1}{{3 a}^{2}}$ $the equation of normal line at point (a, a^{3} - 1)$ $is y = - \frac{1}{{3 a}^{2}} (x - a) + a^{3} - 1 \Rightarrow y = - \frac{x}{{3 a}^{2}} + \frac{1}{3 a} + a^{3} - 1$ $step (2) slope of tangent line curve y^{2} = x - 4 at point$ $Q (b^{2} + 4, b) is m_{2} = \frac{1}{2 b}, then slope of normal$ $line is - 2 b, and the equation of normal line$ $Extra close brace or missing open brace$ $step (3) the both of equation of normal line$ $is same, we get {\begin{cases} - \frac{1}{{3 a}^{2}} = - 2 b; a^{2} b = \frac{1}{6} \\ \frac{1}{3 a} + a^{3} - 1 = {2 b}^{3} + 9 b \end{cases}$ $solving for a and b, \Rightarrow \frac{1}{3 a} + a^{3} - 1 = 2 {(\frac{1}{{6 a}^{2}})}^{3} + 9 (\frac{1}{{6 a}^{2}})$ $\Rightarrow \frac{1}{3 a} + a^{3} - 1 = \frac{1}{{108 a}^{6}} + \frac{3}{{2 a}^{2}}$ ${36 a}^{5} + {108 a}^{9} - {108 a}^{6} = 1 + {162 a}^{4}$ ${108 a}^{9} - {108 a}^{6} + {36 a}^{5} - {162 a}^{4} - 1 = 0$ $we get {\begin{cases} a = 1.2067 \\ b = 0.1145 \end{cases}$ $we get a point P (1.2067; 0.7571) and$ $Q (4.0131; 0.1145)$ $t h e r e f o r e t h e c l o s e s t d i s t a n c e i s$ $Extra close brace or missing open brace$ $∣ P Q ∣ \approx 2.87903$
Commented bybramlexs22 last updated on 09/Mar/21

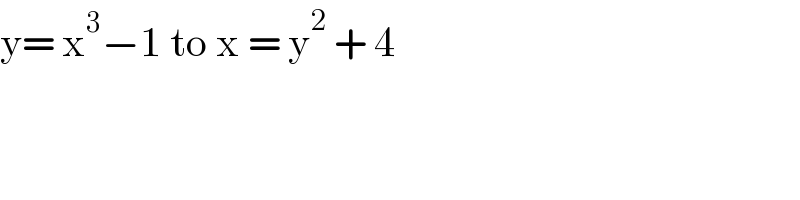
$y = x^{3} - 1 to x = y^{2} + 4$
Commented bybramlexs22 last updated on 10/Mar/21

Commented bymr W last updated on 09/Mar/21
$Edwin sir: please check, i think error is here: is same , we get { ((−(1/(3a^2 )) = −2b ; a^2 b = (1/6))),(((1/(3a))+a^3 −1 = 2b^3 +9b)) :}$
$E d w i n s i r :$ $p l e a s e c h e c k, i t h i n k e r r o r i s h e r e :$ $is same, we get {\begin{cases} - \frac{1}{{3 a}^{2}} = - 2 b; a^{2} b = \frac{1}{6} \\ \frac{1}{3 a} + a^{3} - 1 = {2 b}^{3} + 9 b \end{cases}$
Commented byEDWIN88 last updated on 09/Mar/21

$yes sir . thanks you sir$
	Answered by mr W last updated on 09/Mar/21

	$s a y p o i n t o n c u r v e y = x^{3} - 1 i s$ $P (p, p^{3} - 1)$ $p o i n t o n c u r v e x = y^{2} + 4 i s$ $Q (q^{2} + 4, q)$ $d = P Q$ $D = d^{2} = {(q^{2} + 4 - p)}^{2} + {(q - p^{3} + 1)}^{2}$ $\frac{\partial D}{\partial p} = - 2 (q^{2} + 4 - p) - 6 p^{2} (q - p^{3} + 1) = 0$ $\Rightarrow (q^{2} + 4 - p) + 3 p^{2} (q - p^{3} + 1) = 0 . . . (i)$ $\frac{\partial D}{\partial q} = 4 q (q^{2} + 4 - p) + 2 (q - p^{3} + 1) = 0$ $\Rightarrow 2 q (q^{2} + 4 - p) + (q - p^{3} + 1) = 0 . . . (i i)$ $\Rightarrow 2 q = \frac{1}{3 p^{2}} \Rightarrow q = \frac{1}{6 p^{2}}$ $p u t t h i s i n t o (i) :$ $\frac{1}{36 p^{4}} + 4 - p + 3 p^{2} (\frac{1}{6 p^{2}} - p^{3} + 1) = 0$ $\Rightarrow 108 p^{9} - 108 p^{6} + 36 p^{5} - 162 p^{4} - 1 = 0$ $\Rightarrow p \approx 1 . 2067$ $\Rightarrow d_{m i n} \approx 2 . 8791$
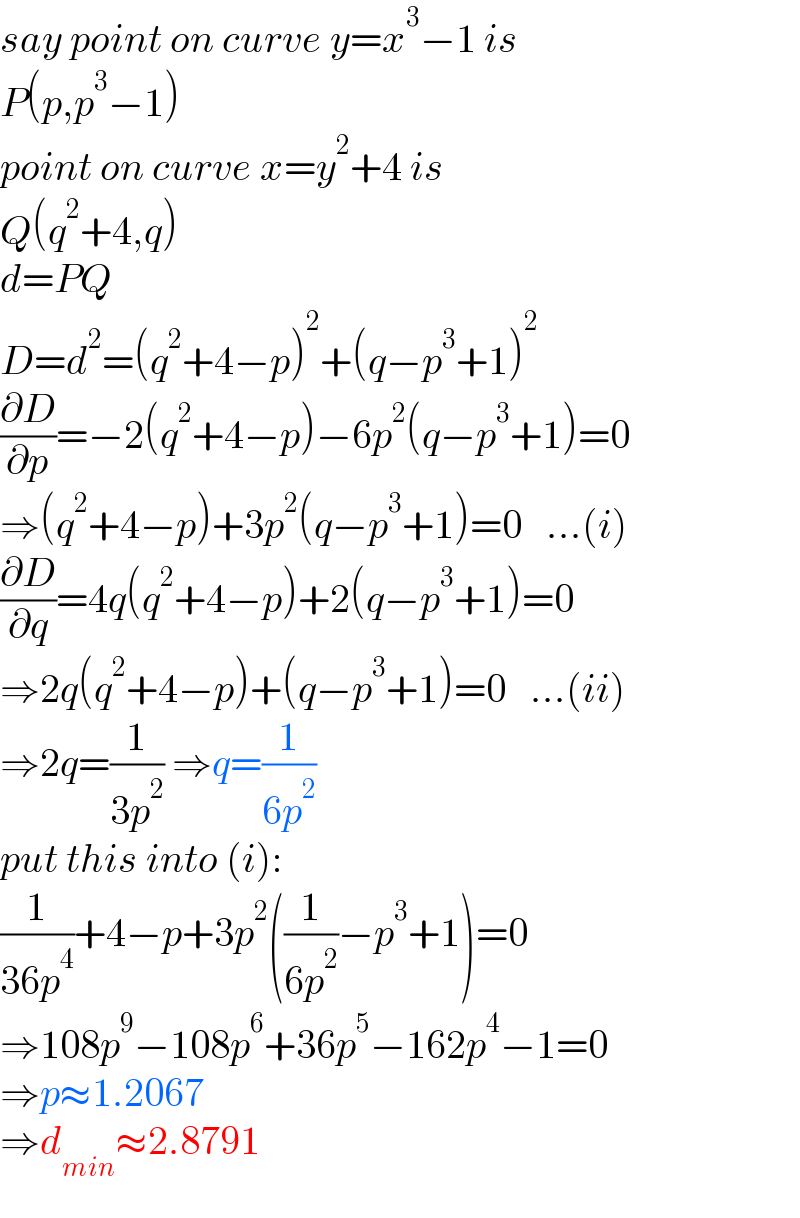
	Commented bymr W last updated on 09/Mar/21

	Commented bybramlexs22 last updated on 09/Mar/21

	$thanks you sir$
Terms of Service
Privacy Policy
Contact: info@tinkutara.com

Question and Answers Forum