
Question and Answers Forum
Question Number 135300 by bobhans last updated on 12/Mar/21
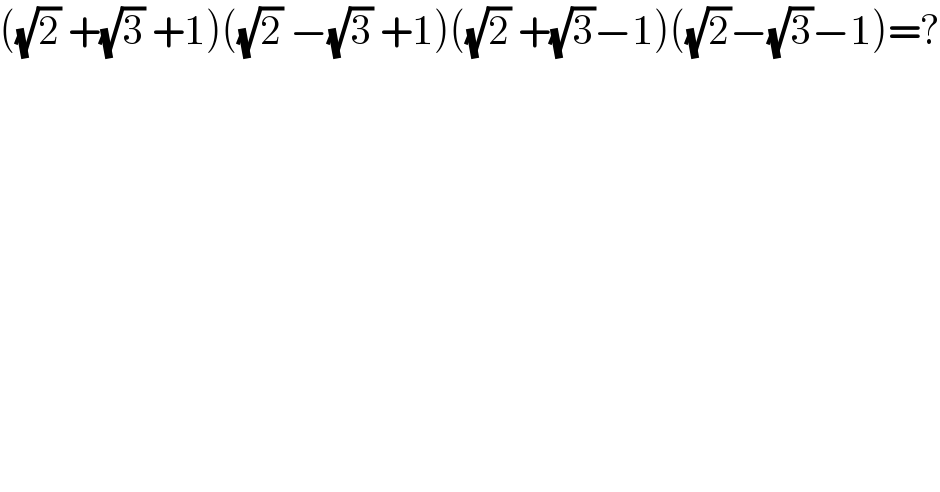
Answered by Olaf last updated on 12/Mar/21
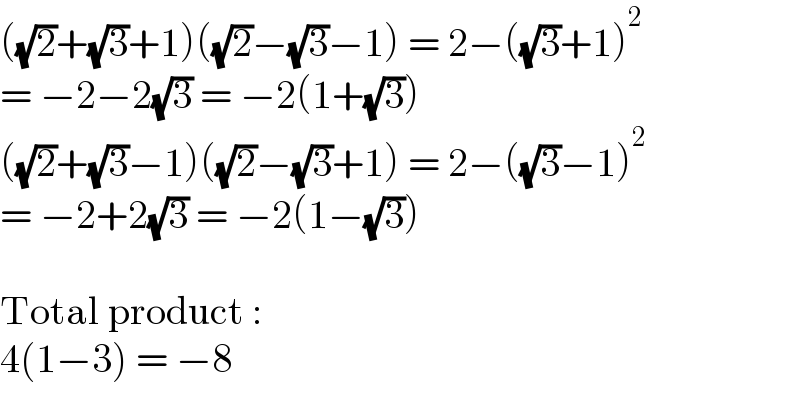
Answered by john_santu last updated on 12/Mar/21
![via Trigonometry let ((√2)+(√3)+1)((√2)−(√3)+1)((√2)+(√3)−1)((√2)−(√3)−1)=p then (((√2)/2)+((√3)/2)+(1/2))(((√2)/2)−((√3)/2)+(1/2))(((√2)/2)+((√3)/2)−(1/2))(((√2)/2)−((√3)/2)−(1/2))=(p/(16)) consider : ((√3)/2)+(1/2)= cos (π/6)+cos (π/3) = 2cos (π/4)cos (π/(12))=(√2) cos (π/(12)) for the first factor ((√2)/2)(1+2cos (π/(12))) for the last factor ((√2)/2)(1−2cos (π/(12))) so the product of these two factors will be (1/2)(1−4cos^2 (π/(12))) likewise for difference of the relevant summands we shall have (1/2)(1−4sin^2 (π/(12))) →now { ((4sin^2 (π/(12)) = 2−(√3))),((4cos^2 (π/(12)) = 2+(√3))) :} ∴ (1/2)(1−4cos^2 (π/(12)))(1−4sin^2 (π/(12)))=(p/(16)) ∴ (1/4)(−1)((√3)−1)((√3)+1)=(p/(16)) ∴ p = 16×(−(1/2))=−8 [ ((√2)+(√3)+1)_(((√2)/2)(1+2cos (π/(12)))) ((√2)−(√3)+1)_(((√2)/2)(1−2cos (π/(12)))) ((√2)+(√3)−1)_(((√2)/2)(1+2sin (π/(12)))) ((√2)−(√3)−1)_(((√2)/2)(1−2sin (π/(12)))) ]](Q135302.png)
Answered by som(math1967) last updated on 12/Mar/21
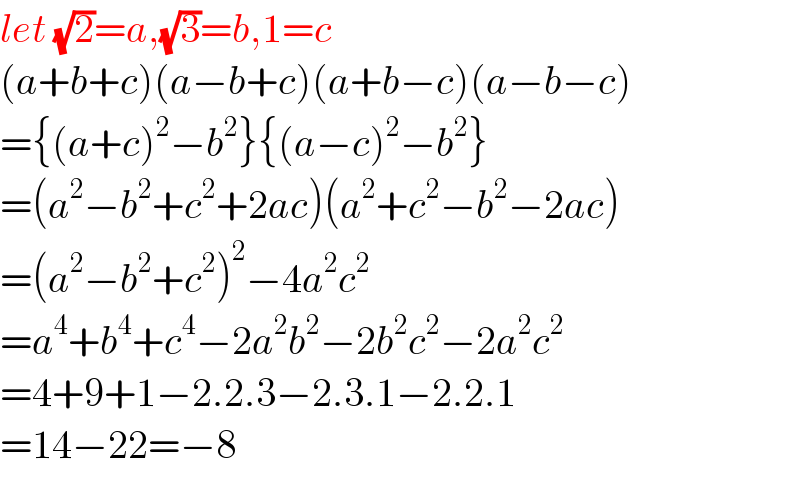
| ||
Question and Answers Forum | ||
Question Number 135300 by bobhans last updated on 12/Mar/21 | ||
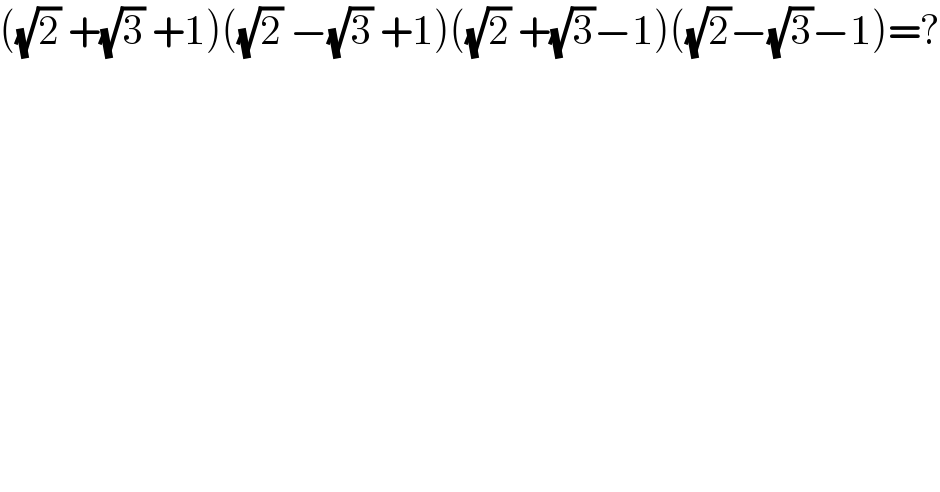 | ||
Answered by Olaf last updated on 12/Mar/21 | ||
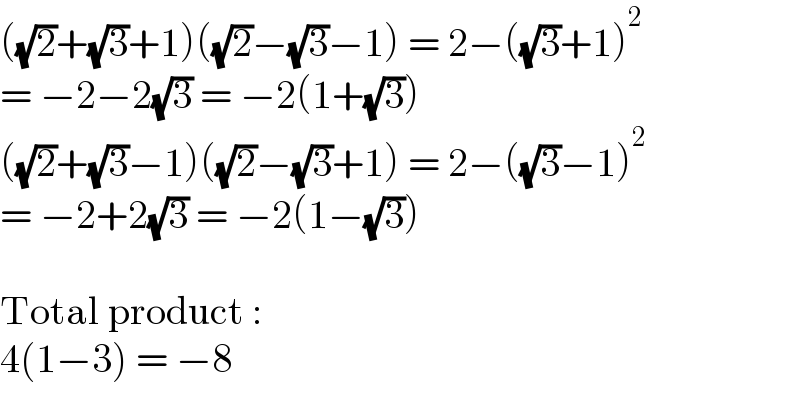 | ||
| ||
Answered by john_santu last updated on 12/Mar/21 | ||
![via Trigonometry let ((√2)+(√3)+1)((√2)−(√3)+1)((√2)+(√3)−1)((√2)−(√3)−1)=p then (((√2)/2)+((√3)/2)+(1/2))(((√2)/2)−((√3)/2)+(1/2))(((√2)/2)+((√3)/2)−(1/2))(((√2)/2)−((√3)/2)−(1/2))=(p/(16)) consider : ((√3)/2)+(1/2)= cos (π/6)+cos (π/3) = 2cos (π/4)cos (π/(12))=(√2) cos (π/(12)) for the first factor ((√2)/2)(1+2cos (π/(12))) for the last factor ((√2)/2)(1−2cos (π/(12))) so the product of these two factors will be (1/2)(1−4cos^2 (π/(12))) likewise for difference of the relevant summands we shall have (1/2)(1−4sin^2 (π/(12))) →now { ((4sin^2 (π/(12)) = 2−(√3))),((4cos^2 (π/(12)) = 2+(√3))) :} ∴ (1/2)(1−4cos^2 (π/(12)))(1−4sin^2 (π/(12)))=(p/(16)) ∴ (1/4)(−1)((√3)−1)((√3)+1)=(p/(16)) ∴ p = 16×(−(1/2))=−8 [ ((√2)+(√3)+1)_(((√2)/2)(1+2cos (π/(12)))) ((√2)−(√3)+1)_(((√2)/2)(1−2cos (π/(12)))) ((√2)+(√3)−1)_(((√2)/2)(1+2sin (π/(12)))) ((√2)−(√3)−1)_(((√2)/2)(1−2sin (π/(12)))) ]](Q135302.png) | ||
| ||
Answered by som(math1967) last updated on 12/Mar/21 | ||
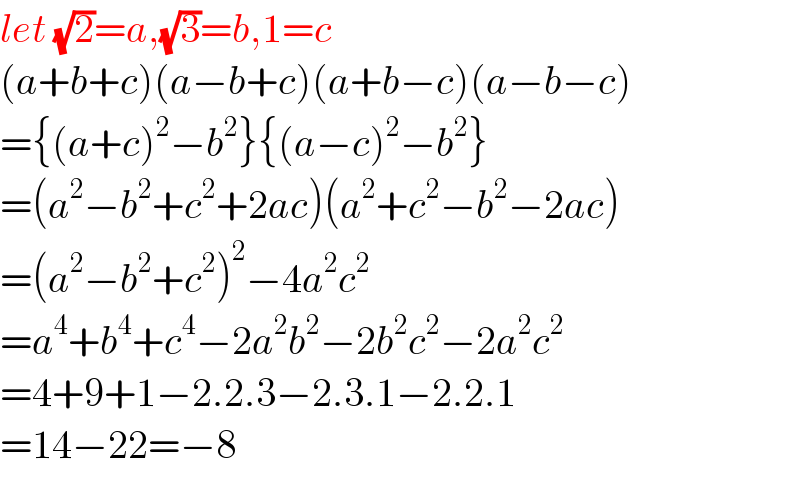 | ||
| ||