
Question Number 1354 by Rasheed Ahmad last updated on 25/Jul/15
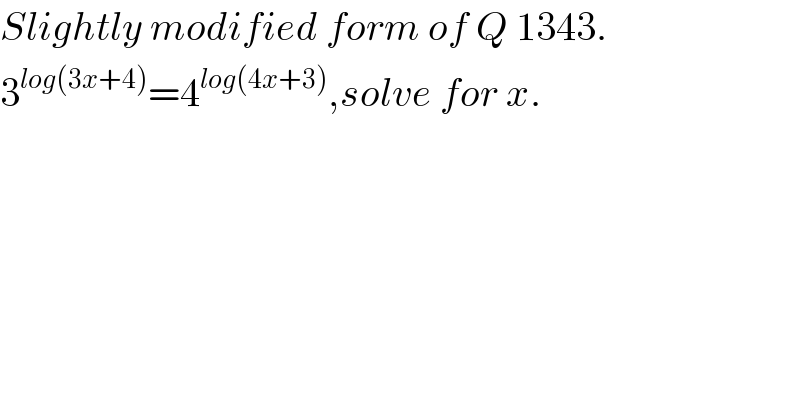
$${Slightly}\:{modified}\:{form}\:{of}\:{Q}\:\mathrm{1343}. \\ $$$$\mathrm{3}^{{log}\left(\mathrm{3}{x}+\mathrm{4}\right)} =\mathrm{4}^{{log}\left(\mathrm{4}{x}+\mathrm{3}\right)} ,{solve}\:{for}\:{x}. \\ $$
Commented by prakash jain last updated on 25/Jul/15

$$\mathrm{One}\:\mathrm{option}\:\mathrm{to}\:\mathrm{prove}\:\mathrm{that}\:{x}=\mathrm{0}\:\mathrm{is}\:\mathrm{the}\:\mathrm{only} \\ $$$$\mathrm{solution}\:\mathrm{for}\:\frac{\mathrm{log}\:\left(\mathrm{3}{x}+\mathrm{4}\right)}{\mathrm{log}\:\left(\mathrm{4}{x}+\mathrm{3}\right)}−\frac{\mathrm{log}\:\mathrm{4}}{\mathrm{log}\:\mathrm{3}}=\mathrm{0}\:\mathrm{is}\:\mathrm{to} \\ $$$$\mathrm{take}\:\mathrm{derivative}\:\mathrm{of}\:\mathrm{the}\:\mathrm{function}. \\ $$$$\mathrm{Also}\:\mathrm{if}\:\mathrm{the}\:\mathrm{function}\:\mathrm{has}\:\mathrm{more}\:\mathrm{than}\:\mathrm{one}\:\mathrm{zero} \\ $$$$\mathrm{it}\:\mathrm{must}\:\mathrm{change}\:\mathrm{sign}\:\mathrm{twice}. \\ $$
Answered by Yugi last updated on 25/Jul/15
![3^(log(3x+4)) =4^(log(4x+3)) .........(1) Taking logs to base 10 on both sides of (1) [log(3x+4)]log3=[log(4x+3)]log4 ⇒((log(3x+4))/(log(4x+3)))=((log4)/(log3))...........(2) Upon observation of theform of (2), the only real solution is x=0 . A graphical approach yields the same result since (1) is equivalent to y=0 for y=3^(log(3x+4)) −4^(log(4x+3)) defined for x>−(3/4). Numerical methods work as well. Otherwise, I could not find an algebraic means of solving for x of the form ((log(ax+b))/(log(cx+d)))=e where all of a,b,c,d and e are non−zero reals.](Q1356.png)
$$\mathrm{3}^{{log}\left(\mathrm{3}{x}+\mathrm{4}\right)} =\mathrm{4}^{{log}\left(\mathrm{4}{x}+\mathrm{3}\right)} .........\left(\mathrm{1}\right) \\ $$$${Taking}\:{logs}\:{to}\:{base}\:\mathrm{10}\:{on}\:{both}\:{sides}\:{of}\:\left(\mathrm{1}\right) \\ $$$$\left[{log}\left(\mathrm{3}{x}+\mathrm{4}\right)\right]{log}\mathrm{3}=\left[{log}\left(\mathrm{4}{x}+\mathrm{3}\right)\right]{log}\mathrm{4} \\ $$$$\Rightarrow\frac{{log}\left(\mathrm{3}{x}+\mathrm{4}\right)}{{log}\left(\mathrm{4}{x}+\mathrm{3}\right)}=\frac{{log}\mathrm{4}}{{log}\mathrm{3}}...........\left(\mathrm{2}\right) \\ $$$${Upon}\:{observation}\:{of}\:{theform}\:{of}\:\left(\mathrm{2}\right),\:{the}\:{only}\:{real}\: \\ $$$${solution}\:{is}\:{x}=\mathrm{0}\:.\:{A}\:{graphical}\:{approach}\:{yields}\: \\ $$$${the}\:{same}\:{result}\:{since}\:\left(\mathrm{1}\right)\:{is}\:{equivalent}\:{to}\:{y}=\mathrm{0}\:{for} \\ $$$${y}=\mathrm{3}^{{log}\left(\mathrm{3}{x}+\mathrm{4}\right)} −\mathrm{4}^{{log}\left(\mathrm{4}{x}+\mathrm{3}\right)} \:{defined}\:{for}\:{x}>−\frac{\mathrm{3}}{\mathrm{4}}. \\ $$$${Numerical}\:{methods}\:{work}\:{as}\:{well}. \\ $$$${Otherwise},\:{I}\:{could}\:{not}\:{find}\:{an}\:{algebraic}\:{means}\: \\ $$$${of}\:{solving}\:{for}\:{x}\:{of}\:{the}\:{form}\: \\ $$$$\frac{{log}\left({ax}+{b}\right)}{{log}\left({cx}+{d}\right)}={e}\:{where}\:{all}\:{of}\:{a},{b},{c},{d}\:{and}\:{e}\:{are} \\ $$$${non}−{zero}\:{reals}. \\ $$
Commented by Rasheed Soomro last updated on 10/Aug/15

$$ \\ $$$${I}\:{appreciate}\:{your}\:{approach}.\:{But}\:{I}\:{am}\:{doubtful}\:{about}\:{your} \\ $$$${claim}\:{that}\:\:{there}\:{is}\:{only}\:{one}\:{real}\:{solution}\:\left({x}=\mathrm{0}\:\right). \\ $$$$\:\:\:\:{You}\:{correctly}\:{derived}\:: \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\frac{{log}\left(\mathrm{3}{x}+\mathrm{4}\right)}{{log}\left(\mathrm{4}{x}+\mathrm{3}\right)}=\frac{{log}\mathrm{4}}{{log}\mathrm{3}} \\ $$$$ \\ $$$$\:\:\:\:\:\:\:{Taking}\:{few}\:\:{steps}\:{more}\:,{we}\:{will}\:{get}, \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:{log}\left(\mathrm{3}{x}+\mathrm{4}\right)=\frac{{log}\:\mathrm{4}}{{log}\:\mathrm{3}}\:.{log}\left(\mathrm{4}{x}+\mathrm{3}\right) \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:={log}\left(\mathrm{4}{x}+\mathrm{3}\right)^{\frac{{log}\:\mathrm{4}}{{log}\:\mathrm{3}}} \\ $$$$\:\:\:\:\:\:\:\:\:{Taking}\:{antilog}\:{of}\:{both}\:{sides} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\mathrm{3}{x}+\mathrm{4}=\left(\mathrm{4}{x}+\mathrm{3}\right)^{\frac{{log}\:\mathrm{4}}{{log}\:\mathrm{3}}} \\ $$$$\:\:\:\:\:\:\:\:{Observe}\:{right}\:{hand}\:{side}\:{the}\:{index}\:\frac{{log}\:\mathrm{4}}{{log}\:\mathrm{3}}\:>\mathrm{0}. \\ $$$$\:\:\:\:\:\:\:\:\:\:{So}\:{for}\:{positive}\:\mathrm{4}{x}+\mathrm{3}\:{theRHS}\:{must}\:{be}\:{real},\:{if}\:{I}\:{am} \\ $$$${not}\:{wrong}.\:{So}\:{I}\:{think}\:{there}\:{may}\:{be}\:{other}\:{real}\:{solution}/{s}\:\:{too}. \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:{I}\:{agree}\:{with}\:{you}\:{that}\:{there}\:{is}\:{no}\:{algebraic}\:{way}\:{to}\:{solve}\: \\ $$$${this}\:{equation}.{But}\:{numerical}\:{methods}\:{may}\:{help}. \\ $$
Commented by Yugi last updated on 25/Jul/15

$${Considering}\:{the}\:{form}\: \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\mathrm{3}{x}+\mathrm{4}=\left(\mathrm{4}{x}+\mathrm{3}\right)^{\frac{{log}\mathrm{4}}{{log}\mathrm{3}}} \:\:\:\:\:........\left(\ast\right) \\ $$$$\frac{{log}\mathrm{4}}{{log}\mathrm{3}}={log}_{\mathrm{3}} \mathrm{4}\:\:{is}\:{an}\:{irrational}\:{exponent}.\:{As}\:{such},\:{the}\:{following}\:\:{numerical}\:{approach}\:{to} \\ $$$${solving}\:{for}\:{x}\:{can}\:{be}\:{done}\:{in}\:{order}\:{to}\:{acquire}\:{a}\:{polynomial}\:{in}\:{x}\:\left({whose}\:{real}\:{solution}\right. \\ $$$$\left.{should}\:{be}\:{found}\:{to}\:{be}\:{approximately}\:{x}=\mathrm{0}\right).\:{Firstly},\:{consider}\:{the}\:{value}\:{of}\:{log}_{\mathrm{3}} \mathrm{4}. \\ $$$${log}_{\mathrm{3}} \mathrm{4}=\mathrm{1}.\mathrm{2618}...\:{So}\:{to}\:\mathrm{2}\:{s}.{f}\:{log}_{\mathrm{3}} \mathrm{4}\approx\mathrm{1}.\mathrm{3}=\frac{\mathrm{13}}{\mathrm{10}} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\therefore\:\:\:\:\:\:\mathrm{3}{x}+\mathrm{4}=\left(\mathrm{4}{x}+\mathrm{3}\right)^{\mathrm{13}/\mathrm{10}} \: \\ $$$${Raising}\:{both}\:{sides}\:{by}\:{the}\:{power}\:{of}\:\mathrm{10}\:{gives} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\left(\mathrm{3}{x}+\mathrm{4}\right)^{\mathrm{10}} =\left(\mathrm{4}{x}+\mathrm{3}\right)^{\mathrm{13}} \\ $$$${While}\:{it}\:{is}\:{possible}\:{to}\:{expand}\:{those}\:{binomials}\:{to}\:{solve}\:{for}\:{x}\:{in}\:{f}\left({x}\right)=\mathrm{0}\:{I}\:{think}\:{it}\:{would}\:{be}\:{easier}\:{to}\:{define} \\ $$$${a}\:{function}\:{y}=\left(\mathrm{3}{x}+\mathrm{4}\right)^{\mathrm{10}} −\left(\mathrm{4}{x}+\mathrm{3}\right)^{\mathrm{13}} \:\:\left({x}>−\mathrm{3}/\mathrm{4},{x}\in\mathbb{R}\right)\:{and}\:{use}\:{numerical}\:{methods} \\ $$$${for}\:{estimating}\:{its}\:{root}.\:{Graphing}\:{yields}\:{an}\:{answer}\:{the}\:{fastest}.\:\: \\ $$$${Now},\:{this}\:{gives}\:{one}\:{estimation}\:{for}\:{x}\:{satisfying}\:\left(\ast\right).\:{To}\:{attain}\:{a}\:{more}\:{accurate} \\ $$$${estimate},\:{use}\:{more}\:{accuarte}\:{rational}\:{approximations}\:{to}\:{log}_{\mathrm{3}} \mathrm{4},\:{such}\:{as}\:\frac{\mathrm{63}}{\mathrm{50}},\frac{\mathrm{6309}}{\mathrm{5000}},\:{etc}. \\ $$$${Every}\:{result}\:{of}\:{x}\:{based}\:{on}\:{these}\:{approximations}\:{have}\:{different}\:{values}\: \\ $$$$\:{but}\:{the}\:{answers}\:{are}\:{near}\:{zero}.\:{What}\:{I}'{ve}\:{outlined}\:{here}\:{is}\:{one}\:{means} \\ $$$${of}\:{obtaining}\:{x}\:{without}\:{knowing}\:{how}\:{many}\:{real}\:{roots}\:{exist}\:{for}\:\left(\ast\right).\:{However}, \\ $$$${in}\:{general},\:{if}\:{x}\:{is}\:{a}\:{negative}\:{real}\:{number}\:{and}\:{y}\:{is}\:{irrational},{then}\:{all}\:{answers}\:{of} \\ $$$${x}^{{y}} \:{are}\:{complex}.\:{Also},\:{if}\:{x}\:{is}\:{positive}\:\left({x}\in\mathbb{R}\right)\:{and}\:{y}\in\bar {\mathbb{Q}}\:{then}\:{x}^{{y}} \:{has}\:{only}\:{one}\:{real} \\ $$$${answer}\:{and}\:{all}\:{of}\:{the}\:{rest}\:{are}\:{complex}.\:{Hence},\:{RHS}\left(\ast\right)\:{should}\:{yield}\:{one}\:{real}\:{result}.\: \\ $$$$\left({Of}\:{course}\:{I}\:{could}\:{be}\:{wrong}.\:{I}\:{did}\:{some}\:{research}\:{but}\:{I}'{m}\:{just}\:{a}\:{student}\:{who}'{s}\:{here}\right. \\ $$$$\left.{to}\:{learn}.\right) \\ $$$$ \\ $$
Commented by Rasheed Soomro last updated on 26/Jul/15

$${I}\:{didn}'{t}\:{say}\:''\:{There}\:{are}\:\boldsymbol{\mathrm{certainly}}\:{more}\:{than}\:{one}\:{soution}\:''. \\ $$$${But}\:{I}\:{said},''\:{There}\:\boldsymbol{\mathrm{may}}\:\boldsymbol{\mathrm{be}}\:{more}\:{than}\:{one}\:{solution}''\:\:{and}\: \\ $$$${suggested}\:{to}\:{confirm}\:{using}\:{numerical}\:{analysis}.{One}\:{other}\: \\ $$$${suggestion}\:{has}\:{come}\:{from}\:{parkash}\:{jain}\:{for}\:{the}\:{confirmation}. \\ $$$$\:\:\:\:\:\:\:\:{But}\:{during}\:{this}\:{comment}\:{I}\:{have}\:{drawn}\:{the}\:{graph}.\boldsymbol{\mathrm{It}}\:\boldsymbol{\mathrm{seems}}\:\boldsymbol{\mathrm{that}}\:\boldsymbol{\mathrm{your}}\:\boldsymbol{\mathrm{claim}}\:\boldsymbol{\mathrm{of}}\:\:''\:\boldsymbol{\mathrm{only}} \\ $$$$\:\boldsymbol{\mathrm{one}}\:\boldsymbol{\mathrm{real}}\:\boldsymbol{\mathrm{solution}}\:\boldsymbol{\mathrm{is}}\:\boldsymbol{\mathrm{correct}}\:''.\: \\ $$$${After}\:{all}\:{we}\:{all}\:{are}\:{learners}. \\ $$$$ \\ $$
Commented by Yugi last updated on 26/Jul/15

$${Yes}.\:{The}\:{graph}\:{showed}\:{the}\:{existence}\:{of}\:{one}\:{real}\:{solution}.\: \\ $$
