
Question Number 135415 by JulioCesar last updated on 13/Mar/21

Commented by liberty last updated on 13/Mar/21
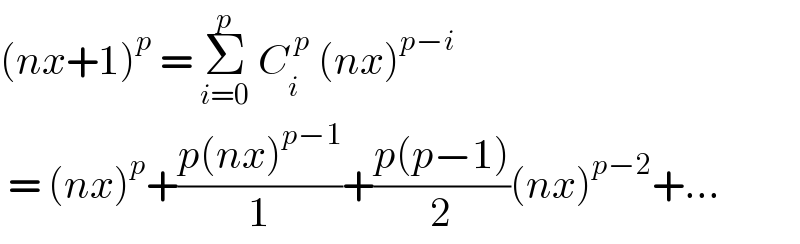
$$\left({nx}+\mathrm{1}\right)^{{p}} \:=\:\underset{{i}=\mathrm{0}} {\overset{{p}} {\sum}}\:{C}_{{i}} ^{\:{p}} \:\left({nx}\right)^{{p}−{i}} \: \\ $$$$\:=\:\left({nx}\right)^{{p}} +\frac{{p}\left({nx}\right)^{{p}−\mathrm{1}} }{\mathrm{1}}+\frac{{p}\left({p}−\mathrm{1}\right)}{\mathrm{2}}\left({nx}\right)^{{p}−\mathrm{2}} +... \\ $$
Answered by SEKRET last updated on 13/Mar/21
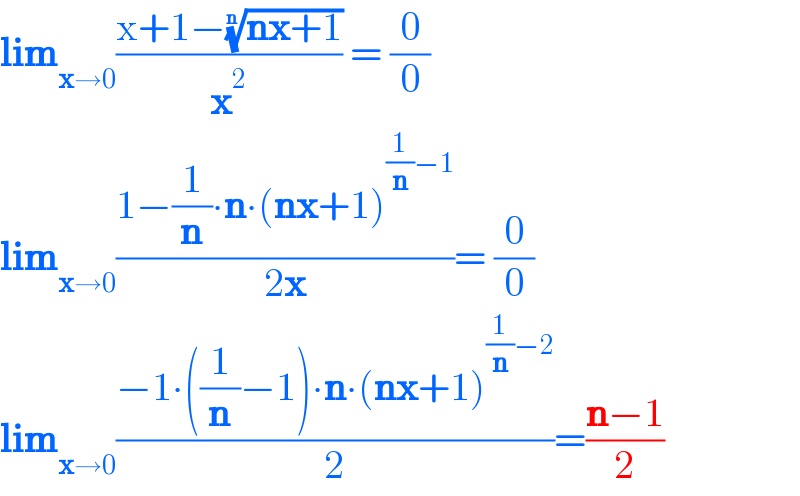
$$\boldsymbol{\mathrm{lim}}_{\boldsymbol{\mathrm{x}}\rightarrow\mathrm{0}} \frac{\mathrm{x}+\mathrm{1}−\sqrt[{\boldsymbol{\mathrm{n}}}]{\boldsymbol{\mathrm{nx}}+\mathrm{1}}}{\boldsymbol{\mathrm{x}}^{\mathrm{2}} }\:=\:\frac{\mathrm{0}}{\mathrm{0}} \\ $$$$\boldsymbol{\mathrm{lim}}_{\boldsymbol{\mathrm{x}}\rightarrow\mathrm{0}} \frac{\mathrm{1}−\frac{\mathrm{1}}{\boldsymbol{\mathrm{n}}}\centerdot\boldsymbol{\mathrm{n}}\centerdot\left(\boldsymbol{\mathrm{nx}}+\mathrm{1}\right)^{\frac{\mathrm{1}}{\boldsymbol{\mathrm{n}}}−\mathrm{1}} }{\mathrm{2}\boldsymbol{\mathrm{x}}}=\:\frac{\mathrm{0}}{\mathrm{0}} \\ $$$$\boldsymbol{\mathrm{lim}}_{\boldsymbol{\mathrm{x}}\rightarrow\mathrm{0}} \frac{−\mathrm{1}\centerdot\left(\frac{\mathrm{1}}{\boldsymbol{\mathrm{n}}}−\mathrm{1}\right)\centerdot\boldsymbol{\mathrm{n}}\centerdot\left(\boldsymbol{\mathrm{nx}}+\mathrm{1}\right)^{\frac{\mathrm{1}}{\boldsymbol{\mathrm{n}}}−\mathrm{2}} }{\mathrm{2}}=\frac{\boldsymbol{\mathrm{n}}−\mathrm{1}}{\mathrm{2}} \\ $$
Answered by SEKRET last updated on 13/Mar/21

$$\boldsymbol{\mathrm{lim}}_{\boldsymbol{\mathrm{x}}\rightarrow\mathrm{0}} \frac{\boldsymbol{\mathrm{x}}+\mathrm{1}−\left(\boldsymbol{\mathrm{x}}+\mathrm{1}+\frac{\left(\mathrm{1}−\boldsymbol{\mathrm{n}}\right)}{\mathrm{2}}\centerdot\boldsymbol{\mathrm{x}}^{\mathrm{2}} +\frac{\left(\boldsymbol{\mathrm{n}}−\mathrm{1}\right)\left(\mathrm{2}\boldsymbol{\mathrm{n}}−\mathrm{1}\right)}{\mathrm{6}}\centerdot\boldsymbol{\mathrm{x}}^{\mathrm{3}} +....\boldsymbol{\mathrm{O}}\left(\boldsymbol{\mathrm{x}}^{\mathrm{5}} \right)\right.}{\boldsymbol{\mathrm{x}}^{\mathrm{2}} }= \\ $$$$=\boldsymbol{\mathrm{im}}_{\boldsymbol{\mathrm{x}}\rightarrow\mathrm{0}} \:\:\left(\frac{\boldsymbol{\mathrm{n}}−\mathrm{2}}{\mathrm{2}}+\frac{\left(\boldsymbol{\mathrm{n}}−\mathrm{1}\right)\left(\mathrm{2}\boldsymbol{\mathrm{n}}−\mathrm{1}\right)}{\mathrm{6}}\boldsymbol{\mathrm{x}}+...\right)= \\ $$$$=\:\:\frac{\boldsymbol{\mathrm{n}}−\mathrm{2}}{\mathrm{2}}+\mathrm{0}+\mathrm{0}+...+\mathrm{0}=\:\frac{\boldsymbol{\mathrm{n}}−\mathrm{2}}{\mathrm{2}} \\ $$
Answered by mathmax by abdo last updated on 13/Mar/21
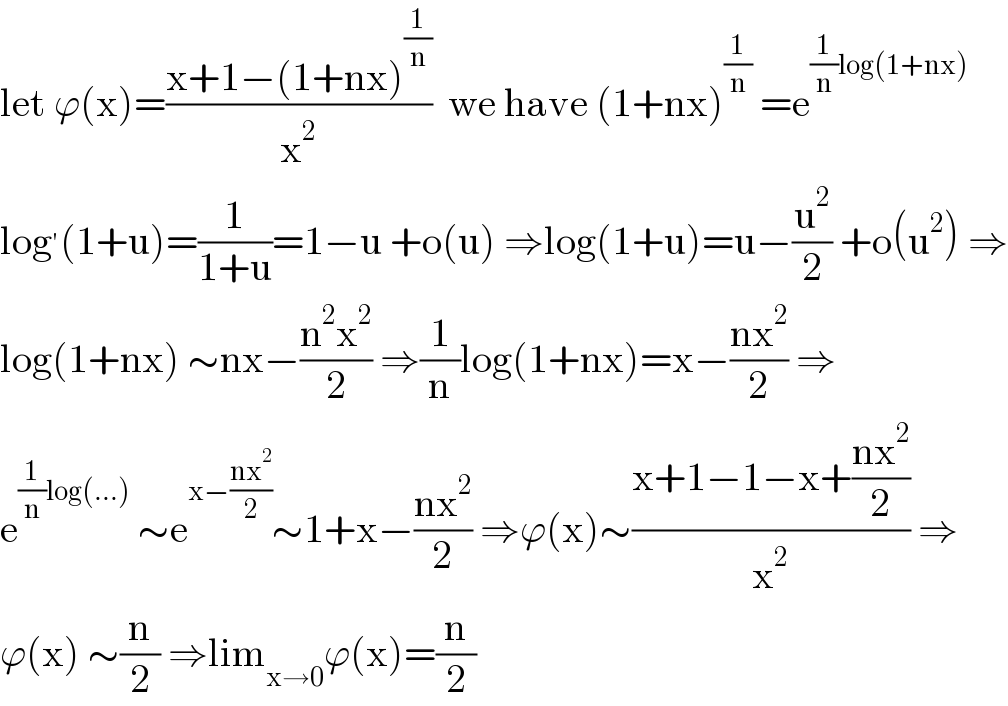
$$\mathrm{let}\:\varphi\left(\mathrm{x}\right)=\frac{\mathrm{x}+\mathrm{1}−\left(\mathrm{1}+\mathrm{nx}\right)^{\frac{\mathrm{1}}{\mathrm{n}}} }{\mathrm{x}^{\mathrm{2}} }\:\:\mathrm{we}\:\mathrm{have}\:\left(\mathrm{1}+\mathrm{nx}\right)^{\frac{\mathrm{1}}{\mathrm{n}}} \:=\mathrm{e}^{\frac{\mathrm{1}}{\mathrm{n}}\mathrm{log}\left(\mathrm{1}+\mathrm{nx}\right)} \\ $$$$\mathrm{log}^{'} \left(\mathrm{1}+\mathrm{u}\right)=\frac{\mathrm{1}}{\mathrm{1}+\mathrm{u}}=\mathrm{1}−\mathrm{u}\:+\mathrm{o}\left(\mathrm{u}\right)\:\Rightarrow\mathrm{log}\left(\mathrm{1}+\mathrm{u}\right)=\mathrm{u}−\frac{\mathrm{u}^{\mathrm{2}} }{\mathrm{2}}\:+\mathrm{o}\left(\mathrm{u}^{\mathrm{2}} \right)\:\Rightarrow \\ $$$$\mathrm{log}\left(\mathrm{1}+\mathrm{nx}\right)\:\sim\mathrm{nx}−\frac{\mathrm{n}^{\mathrm{2}} \mathrm{x}^{\mathrm{2}} }{\mathrm{2}}\:\Rightarrow\frac{\mathrm{1}}{\mathrm{n}}\mathrm{log}\left(\mathrm{1}+\mathrm{nx}\right)=\mathrm{x}−\frac{\mathrm{nx}^{\mathrm{2}} }{\mathrm{2}}\:\Rightarrow \\ $$$$\mathrm{e}^{\frac{\mathrm{1}}{\mathrm{n}}\mathrm{log}\left(...\right)} \:\sim\mathrm{e}^{\mathrm{x}−\frac{\mathrm{nx}^{\mathrm{2}} }{\mathrm{2}}} \sim\mathrm{1}+\mathrm{x}−\frac{\mathrm{nx}^{\mathrm{2}} }{\mathrm{2}}\:\Rightarrow\varphi\left(\mathrm{x}\right)\sim\frac{\mathrm{x}+\mathrm{1}−\mathrm{1}−\mathrm{x}+\frac{\mathrm{nx}^{\mathrm{2}} }{\mathrm{2}}}{\mathrm{x}^{\mathrm{2}} }\:\Rightarrow \\ $$$$\varphi\left(\mathrm{x}\right)\:\sim\frac{\mathrm{n}}{\mathrm{2}}\:\Rightarrow\mathrm{lim}_{\mathrm{x}\rightarrow\mathrm{0}} \varphi\left(\mathrm{x}\right)=\frac{\mathrm{n}}{\mathrm{2}} \\ $$
