Question and Answers Forum

All Questions      Topic List

Number Theory Questions

Previous in All Question      Next in All Question      

Previous in Number Theory      Next in Number Theory      

Question Number 135566 by bemath last updated on 14/Mar/21

Let p,q and r be the distinct roots of the polynomial x^3 −22x^2 +80x−67. There exist real number A,B and C such that (1/(s^3 −22s^2 +80s−67)) = (A/(s−p)) + (B/(s−q)) + (C/(s−r)) for all real numbers s with s ∉ {p,q,r}.What is (1/A) + (1/B) + (1/C) ? (a) 243 (b) 244 (c) 245 (d)246 (e) 247

$${Let}\:{p},{q}\:{and}\:{r}\:{be}\:{the}\:{distinct}\:{roots} \\ $$$${of}\:{the}\:{polynomial}\:{x}^{\mathrm{3}} −\mathrm{22}{x}^{\mathrm{2}} +\mathrm{80}{x}−\mathrm{67}. \\ $$$${There}\:{exist}\:{real}\:{number}\:{A},{B}\:{and} \\ $$$${C}\:{such}\:{that}\:\frac{\mathrm{1}}{{s}^{\mathrm{3}} −\mathrm{22}{s}^{\mathrm{2}} +\mathrm{80}{s}−\mathrm{67}}\:= \\ $$$$\frac{{A}}{{s}−{p}}\:+\:\frac{{B}}{{s}−{q}}\:+\:\frac{{C}}{{s}−{r}}\:{for}\:{all}\:{real}\:{numbers} \\ $$$${s}\:{with}\:{s}\:\notin\:\left\{{p},{q},{r}\right\}.{What}\:{is}\: \\ $$$$\frac{\mathrm{1}}{{A}}\:+\:\frac{\mathrm{1}}{{B}}\:+\:\frac{\mathrm{1}}{{C}}\:? \\ $$$$\left({a}\right)\:\mathrm{243}\:\:\:\:\left({b}\right)\:\mathrm{244}\:\:\:\:\left({c}\right)\:\mathrm{245}\:\:\:\left({d}\right)\mathrm{246} \\ $$$$\left({e}\right)\:\mathrm{247}\: \\ $$

Commented by EDWIN88 last updated on 14/Mar/21

very nice

$$\mathrm{very}\:\mathrm{nice} \\ $$

Answered by EDWIN88 last updated on 14/Mar/21

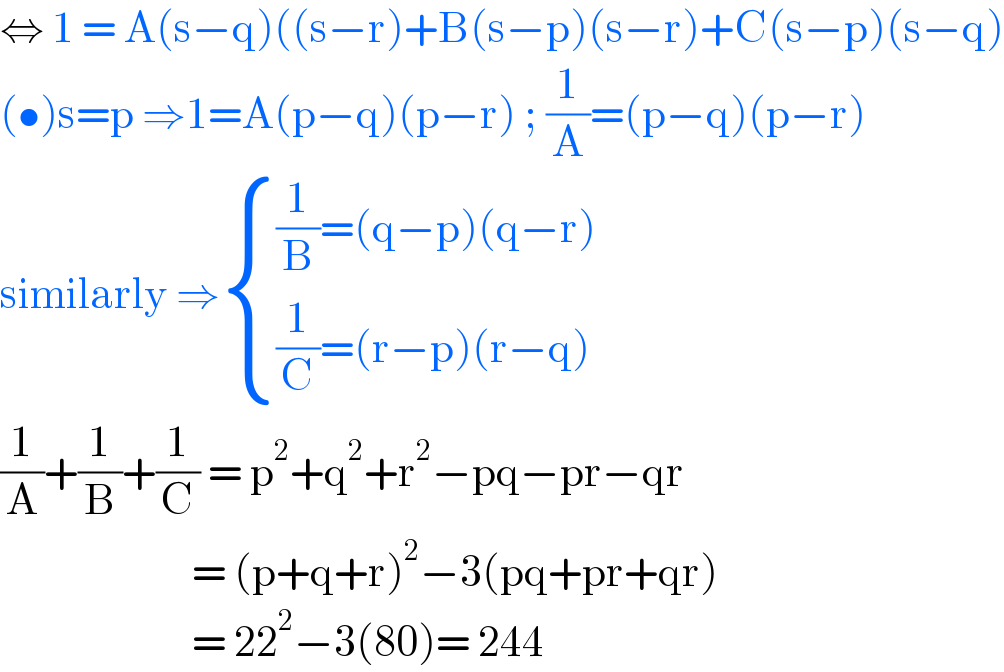
⇔ 1 = A(s−q)((s−r)+B(s−p)(s−r)+C(s−p)(s−q) (•)s=p ⇒1=A(p−q)(p−r) ; (1/A)=(p−q)(p−r) similarly ⇒ { (((1/B)=(q−p)(q−r))),(((1/C)=(r−p)(r−q))) :} (1/A)+(1/B)+(1/C) = p^2 +q^2 +r^2 −pq−pr−qr = (p+q+r)^2 −3(pq+pr+qr) = 22^2 −3(80)= 244

$$\Leftrightarrow\:\mathrm{1}\:=\:\mathrm{A}\left(\mathrm{s}−\mathrm{q}\right)\left(\left(\mathrm{s}−\mathrm{r}\right)+\mathrm{B}\left(\mathrm{s}−\mathrm{p}\right)\left(\mathrm{s}−\mathrm{r}\right)+\mathrm{C}\left(\mathrm{s}−\mathrm{p}\right)\left(\mathrm{s}−\mathrm{q}\right)\right. \\ $$$$\left(\bullet\right)\mathrm{s}=\mathrm{p}\:\Rightarrow\mathrm{1}=\mathrm{A}\left(\mathrm{p}−\mathrm{q}\right)\left(\mathrm{p}−\mathrm{r}\right)\:;\:\frac{\mathrm{1}}{\mathrm{A}}=\left(\mathrm{p}−\mathrm{q}\right)\left(\mathrm{p}−\mathrm{r}\right) \\ $$$$\mathrm{similarly}\:\Rightarrow\begin{cases}{\frac{\mathrm{1}}{\mathrm{B}}=\left(\mathrm{q}−\mathrm{p}\right)\left(\mathrm{q}−\mathrm{r}\right)}\\{\frac{\mathrm{1}}{\mathrm{C}}=\left(\mathrm{r}−\mathrm{p}\right)\left(\mathrm{r}−\mathrm{q}\right)}\end{cases} \\ $$$$\frac{\mathrm{1}}{\mathrm{A}}+\frac{\mathrm{1}}{\mathrm{B}}+\frac{\mathrm{1}}{\mathrm{C}}\:=\:\mathrm{p}^{\mathrm{2}} +\mathrm{q}^{\mathrm{2}} +\mathrm{r}^{\mathrm{2}} −\mathrm{pq}−\mathrm{pr}−\mathrm{qr} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:=\:\left(\mathrm{p}+\mathrm{q}+\mathrm{r}\right)^{\mathrm{2}} −\mathrm{3}\left(\mathrm{pq}+\mathrm{pr}+\mathrm{qr}\right) \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:=\:\mathrm{22}^{\mathrm{2}} −\mathrm{3}\left(\mathrm{80}\right)=\:\mathrm{244} \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com