
Question Number 135571 by bemath last updated on 14/Mar/21
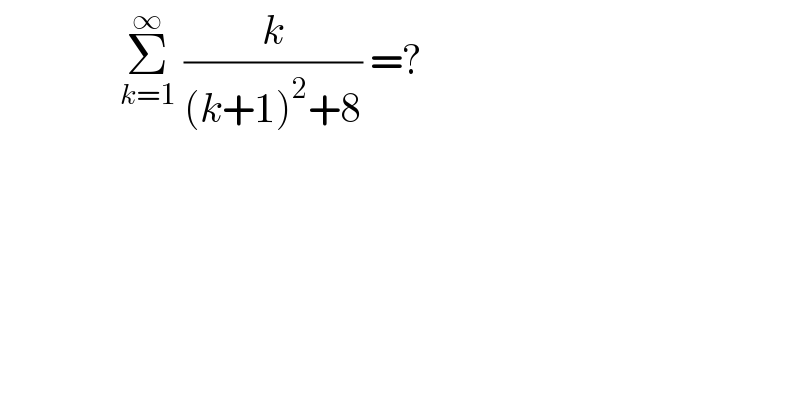
$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\underset{{k}=\mathrm{1}} {\overset{\infty} {\sum}}\:\frac{{k}}{\left({k}+\mathrm{1}\right)^{\mathrm{2}} +\mathrm{8}}\:=? \\ $$
Commented by EDWIN88 last updated on 14/Mar/21

$$\mathrm{i}\:\mathrm{guess}\:\mathrm{the}\:\mathrm{series}\:\mathrm{should}\:\mathrm{be}\:\underset{\mathrm{k}=\mathrm{1}} {\overset{\infty} {\sum}}\:\frac{\mathrm{k}}{\left(\mathrm{k}^{\mathrm{2}} +\mathrm{1}\right)^{\mathrm{2}} +\mathrm{8}} \\ $$
Commented by dhgt last updated on 05/May/21

Answered by mnjuly1970 last updated on 14/Mar/21

$${divergent}... \\ $$
Answered by Dwaipayan Shikari last updated on 14/Mar/21
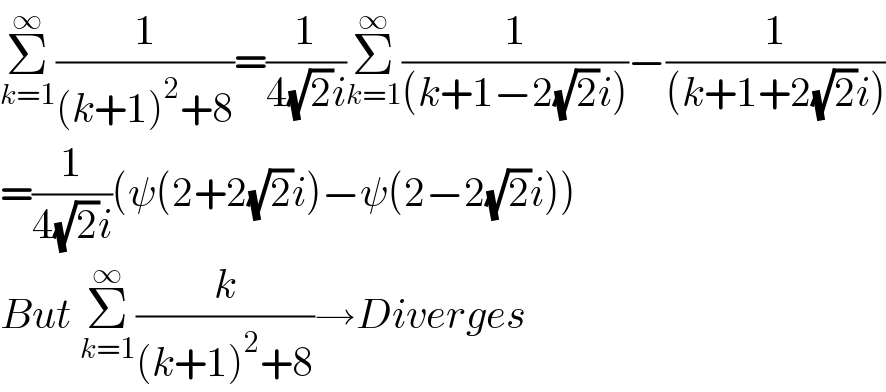
$$\underset{{k}=\mathrm{1}} {\overset{\infty} {\sum}}\frac{\mathrm{1}}{\left({k}+\mathrm{1}\right)^{\mathrm{2}} +\mathrm{8}}=\frac{\mathrm{1}}{\mathrm{4}\sqrt{\mathrm{2}}{i}}\underset{{k}=\mathrm{1}} {\overset{\infty} {\sum}}\frac{\mathrm{1}}{\left({k}+\mathrm{1}−\mathrm{2}\sqrt{\mathrm{2}}{i}\right)}−\frac{\mathrm{1}}{\left({k}+\mathrm{1}+\mathrm{2}\sqrt{\mathrm{2}}{i}\right)} \\ $$$$=\frac{\mathrm{1}}{\mathrm{4}\sqrt{\mathrm{2}}{i}}\left(\psi\left(\mathrm{2}+\mathrm{2}\sqrt{\mathrm{2}}{i}\right)−\psi\left(\mathrm{2}−\mathrm{2}\sqrt{\mathrm{2}}{i}\right)\right) \\ $$$${But}\:\underset{{k}=\mathrm{1}} {\overset{\infty} {\sum}}\frac{{k}}{\left({k}+\mathrm{1}\right)^{\mathrm{2}} +\mathrm{8}}\rightarrow{Diverges} \\ $$
Answered by EDWIN88 last updated on 14/Mar/21
![If Σ_(k=1) ^∞ (k/((k^2 +1)^2 +8)) = Σ_(k=1) ^∞ (k/(k^4 +2k^2 +9)) = Σ_(k=1) ^∞ (k/((k^2 +3)^2 −(2k)^2 )) = Σ_(k=1) ^∞ (k/((k^2 +2k+3)(k^2 −2k+3))) = (1/4)Σ_(k=1) ^∞ (1/(k^2 −2k+3)) − (1/(k^2 +2k+3)) = (1/4) [ (1/2)−(1/6)+(1/3)+(1/6)−(1/(18))+... ] , telescopic series = (1/4)((1/2)+(1/3))= (5/(24))](Q135592.png)
$$\mathrm{If}\:\underset{\mathrm{k}=\mathrm{1}} {\overset{\infty} {\sum}}\:\frac{\mathrm{k}}{\left(\mathrm{k}^{\mathrm{2}} +\mathrm{1}\right)^{\mathrm{2}} +\mathrm{8}}\:=\:\underset{\mathrm{k}=\mathrm{1}} {\overset{\infty} {\sum}}\:\frac{\mathrm{k}}{\mathrm{k}^{\mathrm{4}} +\mathrm{2k}^{\mathrm{2}} +\mathrm{9}} \\ $$$$=\:\underset{\mathrm{k}=\mathrm{1}} {\overset{\infty} {\sum}}\:\frac{\mathrm{k}}{\left(\mathrm{k}^{\mathrm{2}} +\mathrm{3}\right)^{\mathrm{2}} −\left(\mathrm{2k}\right)^{\mathrm{2}} }\:=\:\underset{\mathrm{k}=\mathrm{1}} {\overset{\infty} {\sum}}\:\frac{\mathrm{k}}{\left(\mathrm{k}^{\mathrm{2}} +\mathrm{2k}+\mathrm{3}\right)\left(\mathrm{k}^{\mathrm{2}} −\mathrm{2k}+\mathrm{3}\right)} \\ $$$$=\:\frac{\mathrm{1}}{\mathrm{4}}\underset{\mathrm{k}=\mathrm{1}} {\overset{\infty} {\sum}}\:\frac{\mathrm{1}}{\mathrm{k}^{\mathrm{2}} −\mathrm{2k}+\mathrm{3}}\:−\:\frac{\mathrm{1}}{\mathrm{k}^{\mathrm{2}} +\mathrm{2k}+\mathrm{3}} \\ $$$$=\:\frac{\mathrm{1}}{\mathrm{4}}\:\left[\:\frac{\mathrm{1}}{\mathrm{2}}−\frac{\mathrm{1}}{\mathrm{6}}+\frac{\mathrm{1}}{\mathrm{3}}+\frac{\mathrm{1}}{\mathrm{6}}−\frac{\mathrm{1}}{\mathrm{18}}+...\:\right]\:,\:\mathrm{telescopic}\:\mathrm{series} \\ $$$$=\:\frac{\mathrm{1}}{\mathrm{4}}\left(\frac{\mathrm{1}}{\mathrm{2}}+\frac{\mathrm{1}}{\mathrm{3}}\right)=\:\frac{\mathrm{5}}{\mathrm{24}} \\ $$
