
Question Number 135867 by liberty last updated on 16/Mar/21
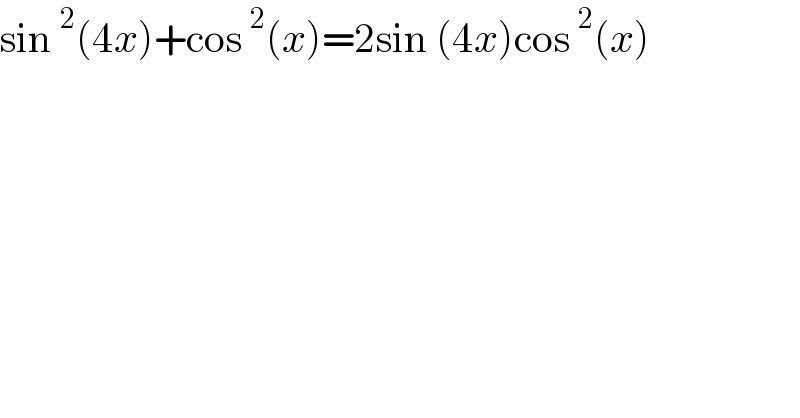
$$\mathrm{sin}\:^{\mathrm{2}} \left(\mathrm{4}{x}\right)+\mathrm{cos}\:^{\mathrm{2}} \left({x}\right)=\mathrm{2sin}\:\left(\mathrm{4}{x}\right)\mathrm{cos}\:^{\mathrm{2}} \left({x}\right) \\ $$$$ \\ $$
Answered by EDWIN88 last updated on 16/Mar/21
![recall cos^2 x = (1/2)+(1/2)cos 2x ⇔ [ 2sin 2x cos 2x ]^2 +(1/2)+(1/2)cos 2x=4sin 2x cos 2x ((1/2)+(1/2)cos 2x) 4sin^2 2x cos^2 2x +(1/2)cos 2x+(1/2)=2sin 2x cos 2x+2sin 2x cos^2 2x 8sin^2 2x cos^2 2x + cos 2x + 1 = 4sin 2x cos 2x +4sin 2x cos^2 2x 8sin^2 2x cos^2 2x+cos 2x+sin^2 2x+cos^2 2x=4sin 2x cos 2x +4sin 2x cos^2 2x](Q135900.png)
$$\mathrm{recall}\:\mathrm{cos}\:^{\mathrm{2}} \mathrm{x}\:=\:\frac{\mathrm{1}}{\mathrm{2}}+\frac{\mathrm{1}}{\mathrm{2}}\mathrm{cos}\:\mathrm{2x} \\ $$$$\Leftrightarrow\:\left[\:\mathrm{2sin}\:\mathrm{2x}\:\mathrm{cos}\:\mathrm{2x}\:\right]^{\mathrm{2}} +\frac{\mathrm{1}}{\mathrm{2}}+\frac{\mathrm{1}}{\mathrm{2}}\mathrm{cos}\:\mathrm{2x}=\mathrm{4sin}\:\mathrm{2x}\:\mathrm{cos}\:\mathrm{2x}\:\left(\frac{\mathrm{1}}{\mathrm{2}}+\frac{\mathrm{1}}{\mathrm{2}}\mathrm{cos}\:\mathrm{2x}\right) \\ $$$$\mathrm{4sin}\:^{\mathrm{2}} \mathrm{2x}\:\mathrm{cos}\:^{\mathrm{2}} \mathrm{2x}\:+\frac{\mathrm{1}}{\mathrm{2}}\mathrm{cos}\:\mathrm{2x}+\frac{\mathrm{1}}{\mathrm{2}}=\mathrm{2sin}\:\mathrm{2x}\:\mathrm{cos}\:\mathrm{2x}+\mathrm{2sin}\:\mathrm{2x}\:\mathrm{cos}\:^{\mathrm{2}} \mathrm{2x} \\ $$$$\mathrm{8sin}\:^{\mathrm{2}} \mathrm{2x}\:\mathrm{cos}\:^{\mathrm{2}} \mathrm{2x}\:+\:\mathrm{cos}\:\mathrm{2x}\:+\:\mathrm{1}\:=\:\mathrm{4sin}\:\mathrm{2x}\:\mathrm{cos}\:\mathrm{2x}\:+\mathrm{4sin}\:\mathrm{2x}\:\mathrm{cos}\:^{\mathrm{2}} \mathrm{2x} \\ $$$$\mathrm{8sin}\:^{\mathrm{2}} \mathrm{2x}\:\mathrm{cos}\:^{\mathrm{2}} \mathrm{2x}+\mathrm{cos}\:\mathrm{2x}+\mathrm{sin}\:^{\mathrm{2}} \mathrm{2x}+\mathrm{cos}\:^{\mathrm{2}} \mathrm{2x}=\mathrm{4sin}\:\mathrm{2x}\:\mathrm{cos}\:\mathrm{2x}\:+\mathrm{4sin}\:\mathrm{2x}\:\mathrm{cos}\:^{\mathrm{2}} \mathrm{2x} \\ $$$$ \\ $$
Answered by liberty last updated on 17/Mar/21

Answered by MJS_new last updated on 17/Mar/21
![using trigonometric formulas I get [sin x =s∧cos x =c] −c^2 (64c^2 s^4 −16s^2 −1)=8c^3 s(2c^2 −1) ⇒ cos x =0 ⇔ ★ x=nπ−(π/2)∧n∈Z ★ −(64c^2 s^4 −16s^2 −1)=8cs(2c^2 −1) this has no real solution](Q135913.png)
$$\mathrm{using}\:\mathrm{trigonometric}\:\mathrm{formulas}\:\mathrm{I}\:\mathrm{get} \\ $$$$\left[\mathrm{sin}\:{x}\:={s}\wedge\mathrm{cos}\:{x}\:={c}\right] \\ $$$$−{c}^{\mathrm{2}} \left(\mathrm{64}{c}^{\mathrm{2}} {s}^{\mathrm{4}} −\mathrm{16}{s}^{\mathrm{2}} −\mathrm{1}\right)=\mathrm{8}{c}^{\mathrm{3}} {s}\left(\mathrm{2}{c}^{\mathrm{2}} −\mathrm{1}\right) \\ $$$$\Rightarrow\:\mathrm{cos}\:{x}\:=\mathrm{0}\:\Leftrightarrow\:\bigstar\:{x}={n}\pi−\frac{\pi}{\mathrm{2}}\wedge{n}\in\mathbb{Z}\:\bigstar \\ $$$$−\left(\mathrm{64}{c}^{\mathrm{2}} {s}^{\mathrm{4}} −\mathrm{16}{s}^{\mathrm{2}} −\mathrm{1}\right)=\mathrm{8}{cs}\left(\mathrm{2}{c}^{\mathrm{2}} −\mathrm{1}\right) \\ $$$$\mathrm{this}\:\mathrm{has}\:\mathrm{no}\:\mathrm{real}\:\mathrm{solution} \\ $$
