Question and Answers Forum

All Questions      Topic List

Differentiation Questions

Previous in All Question      Next in All Question      

Previous in Differentiation      Next in Differentiation      

Question Number 135925 by liberty last updated on 17/Mar/21

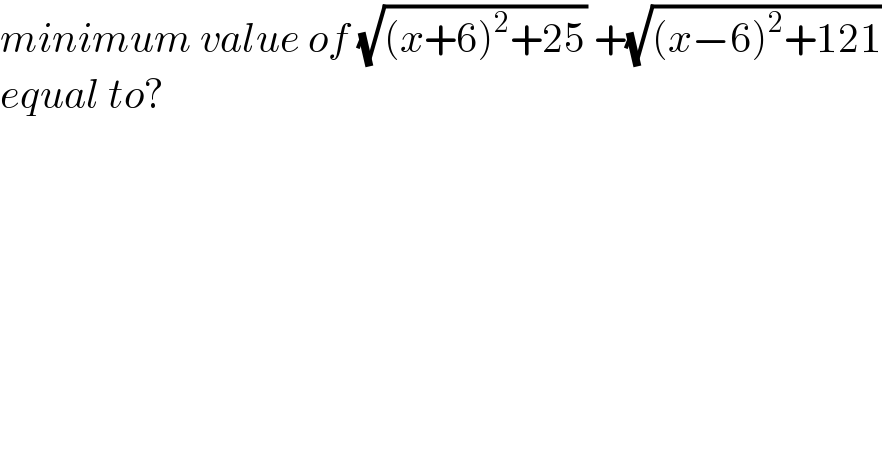
minimum value of (√((x+6)^2 +25)) +(√((x−6)^2 +121)) equal to?

$${minimum}\:{value}\:{of}\:\sqrt{\left({x}+\mathrm{6}\right)^{\mathrm{2}} +\mathrm{25}}\:+\sqrt{\left({x}−\mathrm{6}\right)^{\mathrm{2}} +\mathrm{121}} \\ $$$${equal}\:{to}? \\ $$

Answered by john_santu last updated on 17/Mar/21

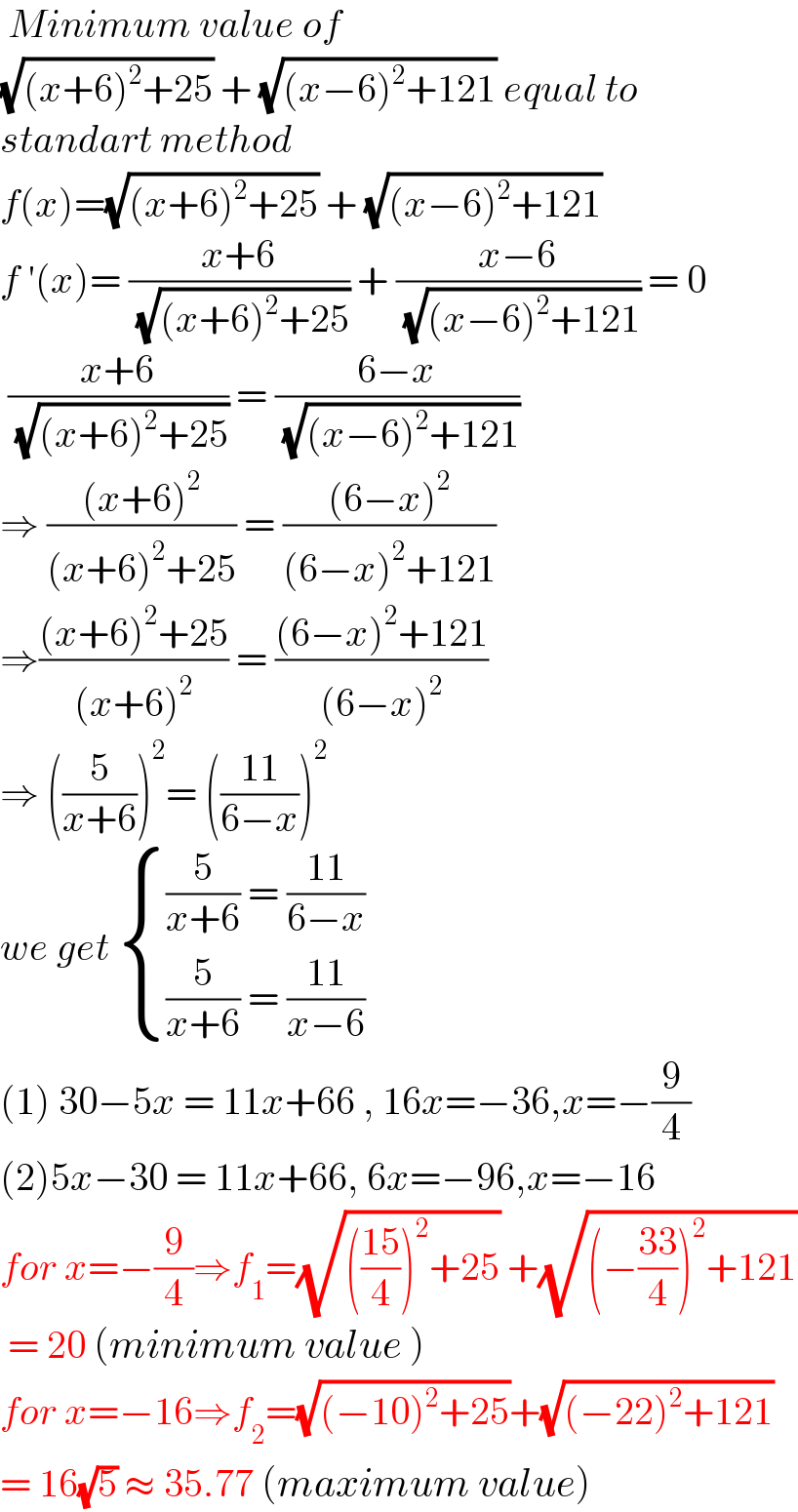
Minimum value of (√((x+6)^2 +25)) + (√((x−6)^2 +121)) equal to standart method f(x)=(√((x+6)^2 +25)) + (√((x−6)^2 +121)) f ′(x)= ((x+6)/( (√((x+6)^2 +25)))) + ((x−6)/( (√((x−6)^2 +121)))) = 0 ((x+6)/( (√((x+6)^2 +25)))) = ((6−x)/( (√((x−6)^2 +121)))) ⇒ (((x+6)^2 )/((x+6)^2 +25)) = (((6−x)^2 )/((6−x)^2 +121)) ⇒(((x+6)^2 +25)/((x+6)^2 )) = (((6−x)^2 +121)/((6−x)^2 )) ⇒ ((5/(x+6)))^2 = (((11)/(6−x)))^2 we get { (((5/(x+6)) = ((11)/(6−x)))),(((5/(x+6)) = ((11)/(x−6)))) :} (1) 30−5x = 11x+66 , 16x=−36,x=−(9/4) (2)5x−30 = 11x+66, 6x=−96,x=−16 for x=−(9/4)⇒f_1 =(√((((15)/4))^2 +25)) +(√((−((33)/4))^2 +121)) = 20 (minimum value ) for x=−16⇒f_2 =(√((−10)^2 +25))+(√((−22)^2 +121)) = 16(√5) ≈ 35.77 (maximum value)

$$\:{Minimum}\:{value}\:{of}\: \\ $$$$\sqrt{\left({x}+\mathrm{6}\right)^{\mathrm{2}} +\mathrm{25}}\:+\:\sqrt{\left({x}−\mathrm{6}\right)^{\mathrm{2}} +\mathrm{121}}\:{equal}\:{to} \\ $$$${standart}\:{method} \\ $$$${f}\left({x}\right)=\sqrt{\left({x}+\mathrm{6}\right)^{\mathrm{2}} +\mathrm{25}}\:+\:\sqrt{\left({x}−\mathrm{6}\right)^{\mathrm{2}} +\mathrm{121}} \\ $$$${f}\:'\left({x}\right)=\:\frac{{x}+\mathrm{6}}{\:\sqrt{\left({x}+\mathrm{6}\right)^{\mathrm{2}} +\mathrm{25}}}\:+\:\frac{{x}−\mathrm{6}}{\:\sqrt{\left({x}−\mathrm{6}\right)^{\mathrm{2}} +\mathrm{121}}}\:=\:\mathrm{0} \\ $$$$\:\frac{{x}+\mathrm{6}}{\:\sqrt{\left({x}+\mathrm{6}\right)^{\mathrm{2}} +\mathrm{25}}}\:=\:\frac{\mathrm{6}−{x}}{\:\sqrt{\left({x}−\mathrm{6}\right)^{\mathrm{2}} +\mathrm{121}}} \\ $$$$\Rightarrow\:\frac{\left({x}+\mathrm{6}\right)^{\mathrm{2}} }{\left({x}+\mathrm{6}\right)^{\mathrm{2}} +\mathrm{25}}\:=\:\frac{\left(\mathrm{6}−{x}\right)^{\mathrm{2}} }{\left(\mathrm{6}−{x}\right)^{\mathrm{2}} +\mathrm{121}} \\ $$$$\Rightarrow\frac{\left({x}+\mathrm{6}\right)^{\mathrm{2}} +\mathrm{25}}{\left({x}+\mathrm{6}\right)^{\mathrm{2}} }\:=\:\frac{\left(\mathrm{6}−{x}\right)^{\mathrm{2}} +\mathrm{121}}{\left(\mathrm{6}−{x}\right)^{\mathrm{2}} } \\ $$$$\Rightarrow\:\left(\frac{\mathrm{5}}{{x}+\mathrm{6}}\right)^{\mathrm{2}} =\:\left(\frac{\mathrm{11}}{\mathrm{6}−{x}}\right)^{\mathrm{2}} \\ $$$${we}\:{get}\:\begin{cases}{\frac{\mathrm{5}}{{x}+\mathrm{6}}\:=\:\frac{\mathrm{11}}{\mathrm{6}−{x}}}\\{\frac{\mathrm{5}}{{x}+\mathrm{6}}\:=\:\frac{\mathrm{11}}{{x}−\mathrm{6}}}\end{cases} \\ $$$$\left(\mathrm{1}\right)\:\mathrm{30}−\mathrm{5}{x}\:=\:\mathrm{11}{x}+\mathrm{66}\:,\:\mathrm{16}{x}=−\mathrm{36},{x}=−\frac{\mathrm{9}}{\mathrm{4}} \\ $$$$\left(\mathrm{2}\right)\mathrm{5}{x}−\mathrm{30}\:=\:\mathrm{11}{x}+\mathrm{66},\:\mathrm{6}{x}=−\mathrm{96},{x}=−\mathrm{16} \\ $$$${for}\:{x}=−\frac{\mathrm{9}}{\mathrm{4}}\Rightarrow{f}_{\mathrm{1}} =\sqrt{\left(\frac{\mathrm{15}}{\mathrm{4}}\right)^{\mathrm{2}} +\mathrm{25}}\:+\sqrt{\left(−\frac{\mathrm{33}}{\mathrm{4}}\right)^{\mathrm{2}} +\mathrm{121}} \\ $$$$\:=\:\mathrm{20}\:\left({minimum}\:{value}\:\right) \\ $$$${for}\:{x}=−\mathrm{16}\Rightarrow{f}_{\mathrm{2}} =\sqrt{\left(−\mathrm{10}\right)^{\mathrm{2}} +\mathrm{25}}+\sqrt{\left(−\mathrm{22}\right)^{\mathrm{2}} +\mathrm{121}} \\ $$$$=\:\mathrm{16}\sqrt{\mathrm{5}}\:\approx\:\mathrm{35}.\mathrm{77}\:\left({maximum}\:{value}\right) \\ $$

Commented by mr W last updated on 17/Mar/21

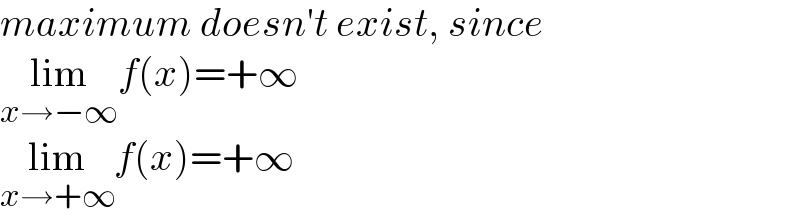
maximum doesn′t exist, since lim_(x→−∞) f(x)=+∞ lim_(x→+∞) f(x)=+∞

$${maximum}\:{doesn}'{t}\:{exist},\:{since} \\ $$$$\underset{{x}\rightarrow−\infty} {\mathrm{lim}}{f}\left({x}\right)=+\infty \\ $$$$\underset{{x}\rightarrow+\infty} {\mathrm{lim}}{f}\left({x}\right)=+\infty \\ $$

Answered by mr W last updated on 17/Mar/21

Commented by mr W last updated on 17/Mar/21

we can solve this problem without using calculus. OA=(√((x+6)^2 +5^2 )) OB=(√((x−6)^2 +11^2 )) mininum from OA+OB is the straight line AB=(√((6+6)^2 +(5+11)^2 )) =20, when the origin is at point C, or x=−(9/4).

$${we}\:{can}\:{solve}\:{this}\:{problem}\:{without} \\ $$$${using}\:{calculus}. \\ $$$${OA}=\sqrt{\left({x}+\mathrm{6}\right)^{\mathrm{2}} +\mathrm{5}^{\mathrm{2}} } \\ $$$${OB}=\sqrt{\left({x}−\mathrm{6}\right)^{\mathrm{2}} +\mathrm{11}^{\mathrm{2}} } \\ $$$${mininum}\:{from}\:{OA}+{OB}\:{is}\:{the} \\ $$$${straight}\:{line}\:{AB}=\sqrt{\left(\mathrm{6}+\mathrm{6}\right)^{\mathrm{2}} +\left(\mathrm{5}+\mathrm{11}\right)^{\mathrm{2}} } \\ $$$$=\mathrm{20},\:{when}\:{the}\:{origin}\:{is}\:{at}\:{point}\:{C},\:{or} \\ $$$${x}=−\frac{\mathrm{9}}{\mathrm{4}}. \\ $$

Commented by mr W last updated on 17/Mar/21

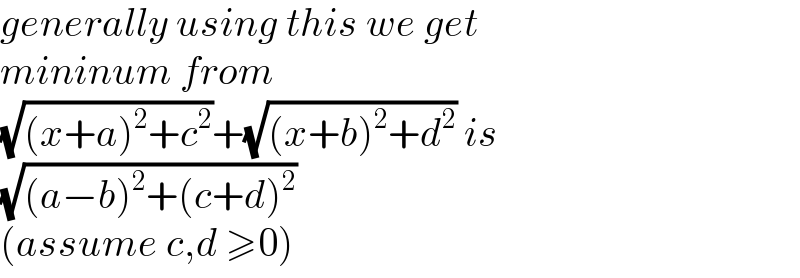
generally using this we get mininum from (√((x+a)^2 +c^2 ))+(√((x+b)^2 +d^2 )) is (√((a−b)^2 +(c+d)^2 )) (assume c,d ≥0)

$${generally}\:{using}\:{this}\:{we}\:{get} \\ $$$${mininum}\:{from} \\ $$$$\sqrt{\left({x}+{a}\right)^{\mathrm{2}} +{c}^{\mathrm{2}} }+\sqrt{\left({x}+{b}\right)^{\mathrm{2}} +{d}^{\mathrm{2}} }\:{is} \\ $$$$\sqrt{\left({a}−{b}\right)^{\mathrm{2}} +\left({c}+{d}\right)^{\mathrm{2}} } \\ $$$$\left({assume}\:{c},{d}\:\geqslant\mathrm{0}\right) \\ $$

Commented by liberty last updated on 17/Mar/21

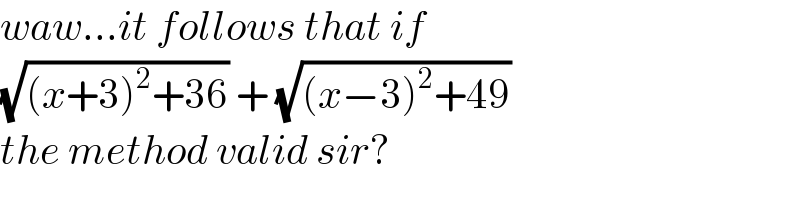
waw...it follows that if (√((x+3)^2 +36)) + (√((x−3)^2 +49)) the method valid sir?

$${waw}...{it}\:{follows}\:{that}\:{if} \\ $$$$\sqrt{\left({x}+\mathrm{3}\right)^{\mathrm{2}} +\mathrm{36}}\:+\:\sqrt{\left({x}−\mathrm{3}\right)^{\mathrm{2}} +\mathrm{49}} \\ $$$${the}\:{method}\:{valid}\:{sir}? \\ $$

Commented by mr W last updated on 17/Mar/21

yes. an other example: [(√((x+3)^2 +10)) + (√((x+8)^2 +20))]_(min) =(√((8−3)^2 +((√(10))+(√(20)))^2 ))=(√(55+20(√2))) you can check it with Grapher or using calculus.

$${yes}. \\ $$$${an}\:{other}\:{example}: \\ $$$$\left[\sqrt{\left({x}+\mathrm{3}\right)^{\mathrm{2}} +\mathrm{10}}\:+\:\sqrt{\left({x}+\mathrm{8}\right)^{\mathrm{2}} +\mathrm{20}}\right]_{{min}} \\ $$$$=\sqrt{\left(\mathrm{8}−\mathrm{3}\right)^{\mathrm{2}} +\left(\sqrt{\mathrm{10}}+\sqrt{\mathrm{20}}\right)^{\mathrm{2}} }=\sqrt{\mathrm{55}+\mathrm{20}\sqrt{\mathrm{2}}} \\ $$$${you}\:{can}\:{check}\:{it}\:{with}\:{Grapher}\:{or} \\ $$$${using}\:{calculus}. \\ $$

Commented by liberty last updated on 17/Mar/21

great....

$${great}.... \\ $$

Commented by Dwaipayan Shikari last updated on 17/Mar/21

Newton used to have Geometrical Method of Calculus

$${Newton}\:{used}\:{to}\:{have}\:{Geometrical}\:{Method}\:{of}\:{Calculus} \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com