
Question and Answers Forum
Question Number 135932 by Engr_Jidda last updated on 17/Mar/21
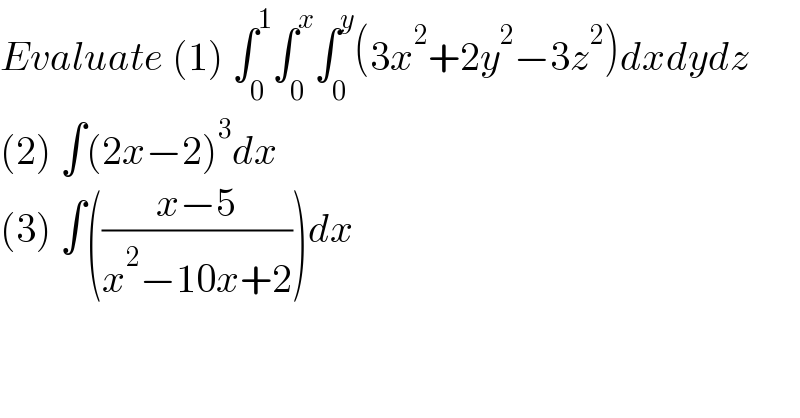
Answered by Olaf last updated on 17/Mar/21
![1) Ω = ∫_0 ^1 ∫_0 ^x ∫_0 ^y (3x^2 +2y^2 −3z^2 )dxdydz Ω = ∫_0 ^1 ∫_0 ^x [3x^2 z+2y^2 z−z^3 ]_0 ^y dxdy Ω = ∫_0 ^1 ∫_0 ^x (3x^2 y+y^3 )dxdy Ω = ∫_0 ^1 [(3/2)x^2 y^2 +(y^4 /4)]_0 ^x dx Ω = ∫_0 ^1 (7/4)x^4 dx = (7/4) 2) ∫(2x−2)^3 dx = (1/8)(2x−2)^4 +C = 2(x−1)^4 +C 3) ∫((x−5)/(x^2 −10x+2))dx = (1/2)∫ ((d(x^2 −10x+2))/(x^2 −10x+2)) = (1/2)ln∣x^2 −10x+2∣+C](Q135938.png)
Answered by Ar Brandon last updated on 17/Mar/21
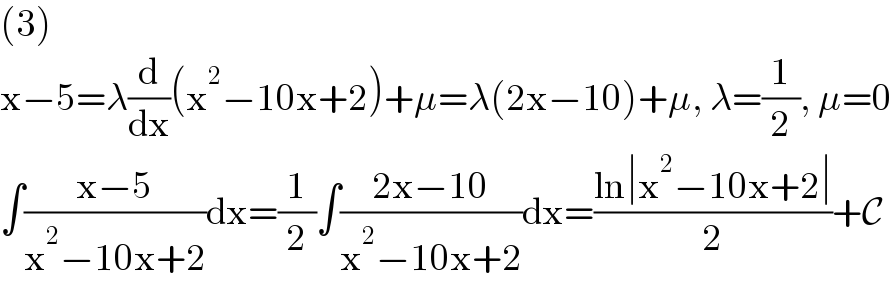
| ||
Question and Answers Forum | ||
Question Number 135932 by Engr_Jidda last updated on 17/Mar/21 | ||
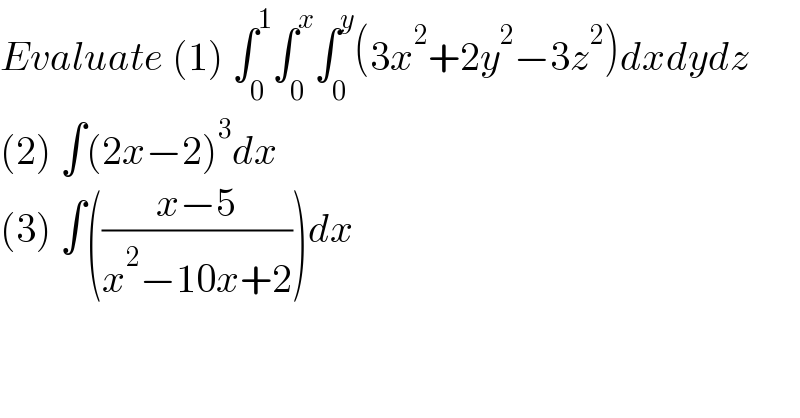 | ||
Answered by Olaf last updated on 17/Mar/21 | ||
![1) Ω = ∫_0 ^1 ∫_0 ^x ∫_0 ^y (3x^2 +2y^2 −3z^2 )dxdydz Ω = ∫_0 ^1 ∫_0 ^x [3x^2 z+2y^2 z−z^3 ]_0 ^y dxdy Ω = ∫_0 ^1 ∫_0 ^x (3x^2 y+y^3 )dxdy Ω = ∫_0 ^1 [(3/2)x^2 y^2 +(y^4 /4)]_0 ^x dx Ω = ∫_0 ^1 (7/4)x^4 dx = (7/4) 2) ∫(2x−2)^3 dx = (1/8)(2x−2)^4 +C = 2(x−1)^4 +C 3) ∫((x−5)/(x^2 −10x+2))dx = (1/2)∫ ((d(x^2 −10x+2))/(x^2 −10x+2)) = (1/2)ln∣x^2 −10x+2∣+C](Q135938.png) | ||
| ||
Answered by Ar Brandon last updated on 17/Mar/21 | ||
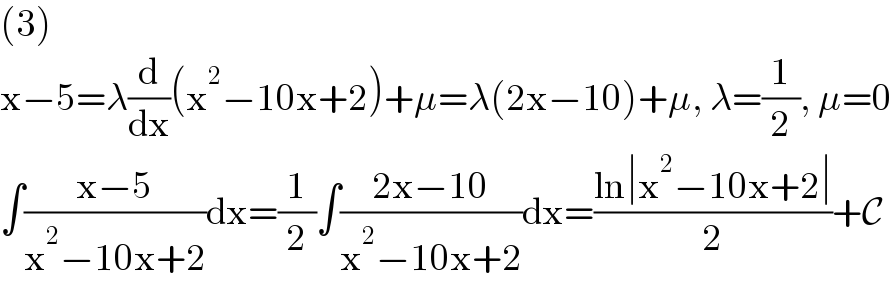 | ||
| ||