
Question and Answers Forum
Question Number 136076 by physicstutes last updated on 18/Mar/21
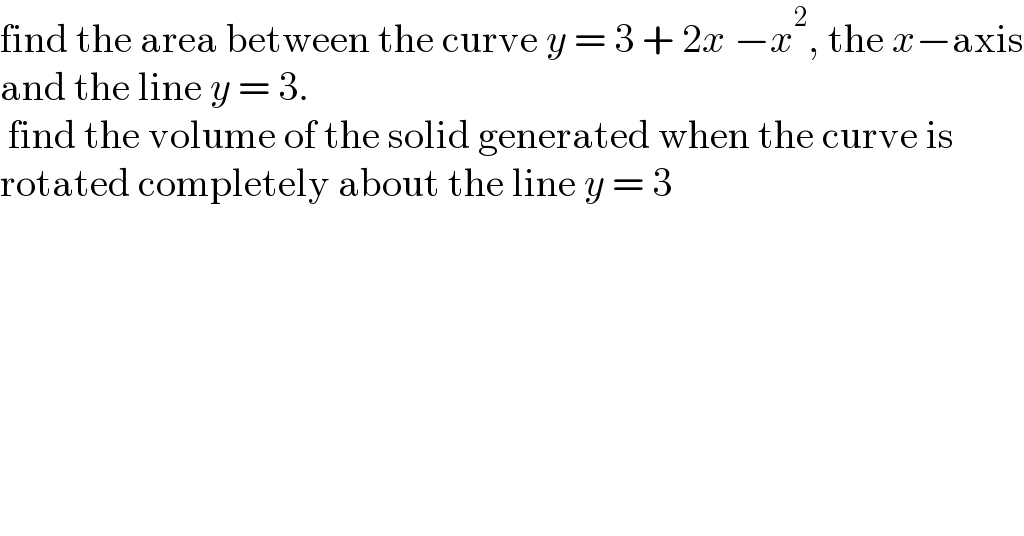
Answered by mr W last updated on 18/Mar/21
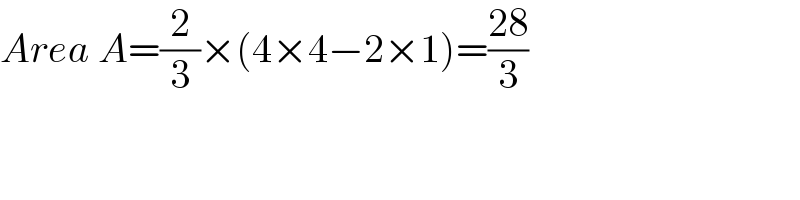
Commented by mr W last updated on 18/Mar/21
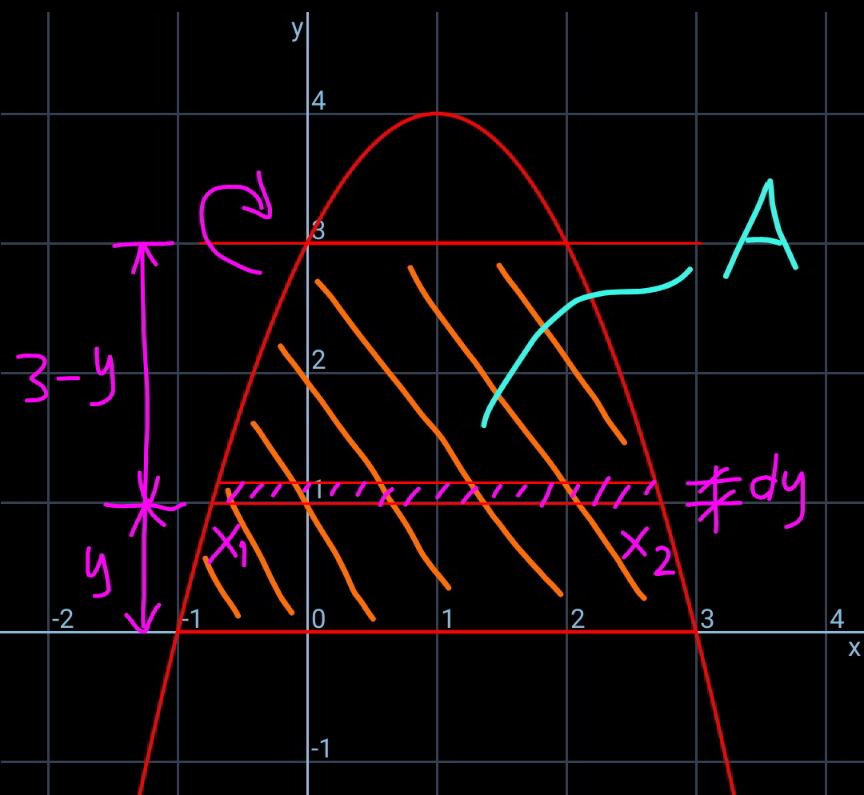
Commented by mr W last updated on 18/Mar/21
![volume V x^2 −2x−3+y=0 (x_2 −x_1 )^2 =(x_2 +x_1 )^2 −4x_1 x_2 =2^2 −4(−3+y)=4(4−y) x_2 −x_1 =2(√(4−y)) dV=2π(3−y)(x_2 −x_1 )dy V=∫_0 ^3 2π(3−y)(x_2 −x_1 )dy =4π∫_0 ^3 (3−y)(√(4−y))dy =4π∫_3 ^0 (3−y)(√(1+3−y))d(3−y) =4π∫_0 ^3 u(√(1+u))du =4π×(2/(15))[(u+1)^(3/2) (3u−2)]_0 ^3 =4π×((2×58)/(15)) =((464π)/(15))](Q136097.png)
| ||
Question and Answers Forum | ||
Question Number 136076 by physicstutes last updated on 18/Mar/21 | ||
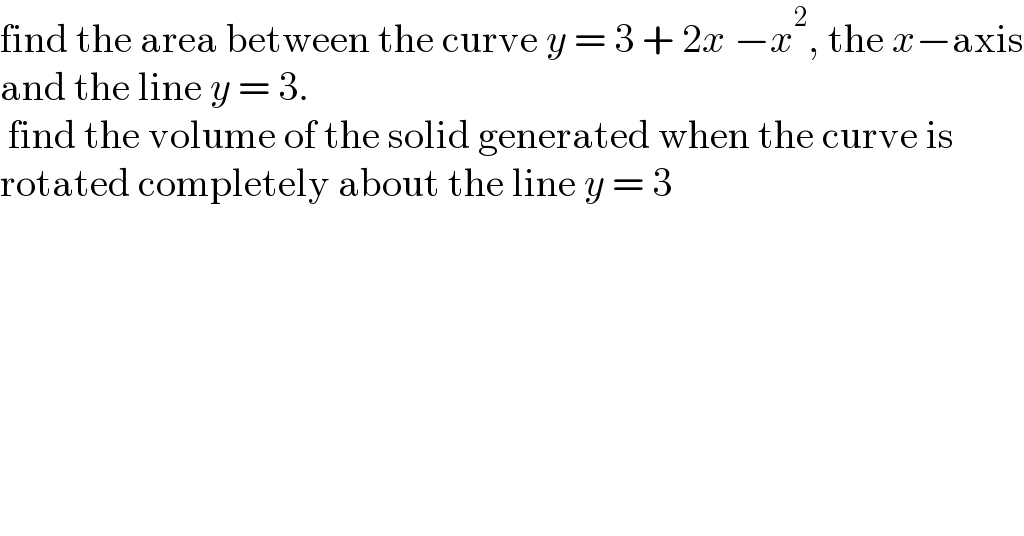 | ||
Answered by mr W last updated on 18/Mar/21 | ||
 | ||
| ||
Commented by mr W last updated on 18/Mar/21 | ||
 | ||
Commented by mr W last updated on 18/Mar/21 | ||
![volume V x^2 −2x−3+y=0 (x_2 −x_1 )^2 =(x_2 +x_1 )^2 −4x_1 x_2 =2^2 −4(−3+y)=4(4−y) x_2 −x_1 =2(√(4−y)) dV=2π(3−y)(x_2 −x_1 )dy V=∫_0 ^3 2π(3−y)(x_2 −x_1 )dy =4π∫_0 ^3 (3−y)(√(4−y))dy =4π∫_3 ^0 (3−y)(√(1+3−y))d(3−y) =4π∫_0 ^3 u(√(1+u))du =4π×(2/(15))[(u+1)^(3/2) (3u−2)]_0 ^3 =4π×((2×58)/(15)) =((464π)/(15))](Q136097.png) | ||