Question and Answers Forum

All Questions      Topic List

Integration Questions

Previous in All Question      Next in All Question      

Previous in Integration      Next in Integration      

Question Number 136210 by Ar Brandon last updated on 19/Mar/21

$$\mathrm{Show}\mathrm{that}{\int }_0^{\mathrm{\infty }}\frac{\mathrm{lnx}}{{({\mathrm{x}}^2+1)}^2}\mathrm{dx}=-\frac{\pi }{4}$$

Commented by Ar Brandon last updated on 19/Mar/21

$$\mathrm{Oh}!\mathrm{Thank}\mathrm{You}\mathrm{Sir}$$😃

Commented by Ar Brandon last updated on 19/Mar/21

$$\mathrm{\Omega }={\int }_0^{\mathrm{\infty }}\frac{\mathrm{lnx}}{{({\mathrm{x}}^2+1)}^2}\mathrm{dx}$$$$=\frac{\partial }{\partial \mathrm{s}}{\mid }_{\mathrm{s}=0}{\int }_0^{\mathrm{\infty }}\frac{{\mathrm{x}}^{\mathrm{s}}}{{({\mathrm{x}}^2+1)}^2}\mathrm{dx}\stackrel{\mathrm{u}={\mathrm{x}}^2}{=}\frac{\partial }{\partial \mathrm{s}}{\mid }_{\mathrm{s}=0}\frac{1}{2}{\int }_0^{\mathrm{\infty }}\frac{{\mathrm{u}}^{\frac{\mathrm{s}}{2}-\frac{1}{2}}}{{(\mathrm{u}+1)}^2}\mathrm{du}$$$$=\frac{\partial }{\partial \mathrm{s}}{\mid }_{\mathrm{s}=0}\frac{1}{2}\beta (\frac{\mathrm{s}}{2}+\frac{1}{2},\frac{3}{2}-\frac{\mathrm{s}}{2})=\frac{\partial }{\partial \mathrm{s}}{\mid }_{\mathrm{s}=0}\frac{1}{2}\mathrm{\Gamma }(\frac{\mathrm{s}}{2}+\frac{1}{2})\mathrm{\Gamma }(\frac{3}{2}-\frac{\mathrm{s}}{2})$$$$=\frac{1}{2}{\mid }_{\mathrm{s}=0}\mathrm{\Gamma }(\frac{\mathrm{s}}{2}+\frac{1}{2}){\mathrm{\Gamma }}^{\prime }(\frac{3}{2}-\frac{\mathrm{s}}{2})+\mathrm{\Gamma }(\frac{3}{2}-\frac{\mathrm{s}}{2}){\mathrm{\Gamma }}^{\prime }(\frac{\mathrm{s}}{2}+\frac{1}{2})$$$$=\frac{1}{2}\cdot \frac{1}{2}\mathrm{\Gamma }\left(\frac{1}{2}\right)\mathrm{\Gamma }\left(\frac{3}{2}\right)[\psi \left(\frac{1}{2}\right)-\psi \left(\frac{3}{2}\right)]=\frac{\pi }{8}[\psi \left(\frac{1}{2}\right)-\psi \left(\frac{1}{2}\right)-2]=-\frac{\pi }{4}$$

Commented by mnjuly1970 last updated on 19/Mar/21

$$errorinsignofdrivative$$$$of\psi (\frac{3}{2}-s).......{}^{\prime }=-{\psi }^{\prime }(\frac{3}{2}-s)$$$$...goodluckmybrothermrbrandon...$$

Answered by mnjuly1970 last updated on 19/Mar/21

$$\mathit{\varphi }\stackrel{x^2=y}{=}\frac{1}{4}{\int }_0^{\mathrm{\infty }}\frac{y^{-\frac{1}{2}}ln\left(y\right)}{{(y+1)}^2}dy$$$$f\left(a\right)={\int }_0^{\mathrm{\infty }}\frac{y^{a-\frac{1}{2}}}{{(y+1)}^2}dy$$$$\mathit{\varphi }=\frac{f{}^{\prime }\left(0\right)}{4}...✓$$$$f\left(a\right)={\int }_0^{\mathrm{\infty }}\frac{y^{a+\frac{1}{2}-1}}{{(y+1)}^2}dy=\beta (a+\frac{1}{2},\frac{3}{2}-a)$$$$f\left(a\right)=\mathrm{\Gamma }(a+\frac{1}{2}).\mathrm{\Gamma }(\frac{3}{2}-a)$$$$f{}^{\prime }\left(a\right)={\mathrm{\Gamma }}^{\prime }(a+\frac{1}{2})\mathrm{\Gamma }(\frac{3}{2}-a)-{\mathrm{\Gamma }}^{\prime }(\frac{3}{2}-a)\mathrm{\Gamma }(\frac{1}{2}+a)$$$$\mathit{\varphi }=\frac{1}{4}f{}^{\prime }\left(0\right)=\frac{1}{4}(\frac{1}{2}\psi \left(\frac{1}{2}\right){\mathrm{\Gamma }}^2\left(\frac{1}{2}\right)-\frac{1}{2}\psi \left(\frac{3}{2}\right){\mathrm{\Gamma }}^2\left(\frac{1}{2}\right))$$$$=\frac{\pi }{8}(\psi \left(\frac{1}{2}\right)-\psi \left(\frac{3}{2}\right))$$$$=\frac{\pi }{8}(\psi \left(\frac{1}{2}\right)-\psi \left(\frac{1}{2}\right)-2)=\frac{-\pi }{4}..✓✓$$$$$$

Answered by Dwaipayan Shikari last updated on 19/Mar/21

$$\frac{1}{4}{\int }_0^{\mathrm{\infty }}\frac{u^{-\frac{1}{2}}log\left(u\right)}{{(1+u)}^2}du=\frac{1}{4}{\tau }^{\prime }\left(\frac{1}{2}\right)={\int }_0^{\mathrm{\infty }}\frac{log\left(x\right)}{{(x^2+1)}^2}dx$$$$\tau \left(\alpha \right)={\int }_0^{\mathrm{\infty }}\frac{u^{\alpha -1}}{{(1+u)}^2}du=\frac{\mathrm{\Gamma }\left(\alpha \right)\mathrm{\Gamma }(2-\alpha )}{\mathrm{\Gamma }\left(2\right)}=\frac{\pi (1-\alpha )}{sin\left(\pi \alpha \right)}$$$$\Rightarrow {\tau }^{\prime }\left(\alpha \right)={\int }_0^{\mathrm{\infty }}\frac{u^{\alpha -1}log\left(u\right)}{{(1+u)}^2}du=-{\pi }^{2}cosec\left(\pi \alpha \right)cot\left(\pi \alpha \right)-\frac{\pi }{sin\left(\pi \alpha \right)}$$$$\frac{1}{4}{\tau }^{\prime }\left(\frac{1}{2}\right)=-0-\frac{\pi }{4}=-\frac{\pi }{4}$$

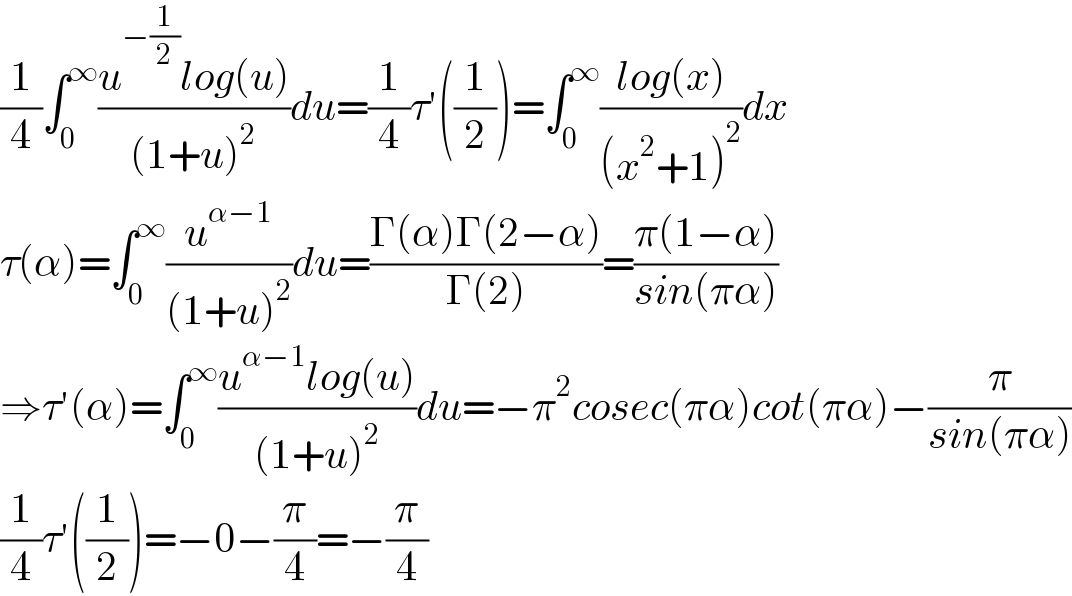
Commented by Ar Brandon last updated on 19/Mar/21

$$\mathrm{Thanks}\mathrm{bro}$$

Commented by Dwaipayan Shikari last updated on 19/Mar/21

$$$$😃

Answered by Ajetunmobi last updated on 19/Mar/21

$$$$$$\mathbf{i}\mathbf{have}\mathbf{drop}\mathbf{the}\mathbf{solution}\mathbf{before}\mathbf{here}$$

Commented by Ar Brandon last updated on 19/Mar/21

$$\mathrm{Alright}!$$$$\mathrm{Before}\mathrm{posting}\mathrm{I}\mathrm{used}\mathrm{the}\mathrm{search}\mathrm{option}$$$$\mathrm{to}\mathrm{check}\mathrm{if}\mathrm{it}\mathrm{was}\mathrm{previously}\mathrm{posted}\mathrm{but}$$$${\mathrm{couldn}}^{\prime }\mathrm{t}\mathrm{find}\mathrm{it}.\mathrm{Thank}\mathrm{You}\mathrm{Sir}$$

Commented by Ajetunmobi last updated on 19/Mar/21

$$$$$$\mathbf{ok}$$

Answered by Ajetunmobi last updated on 19/Mar/21

Answered by mathmax by abdo last updated on 19/Mar/21

$$\mathrm{let}\mathrm{f}\left(\mathrm{a}\right)={\int }_0^{\mathrm{\infty }}\frac{\mathrm{lnx}}{{\mathrm{x}}^2+{\mathrm{a}}^2}\mathrm{dx}\mathrm{with}\mathrm{a}>0\Rightarrow {\mathrm{f}}^{{}^{\prime }}\left(\mathrm{a}\right)=-2\mathrm{a}{\int }_0^{\mathrm{\infty }}\frac{\mathrm{lnx}}{{({\mathrm{x}}^2+{\mathrm{a}}^2)}^2}\mathrm{dx}\Rightarrow$$$${\mathrm{f}}^{{}^{\prime }}\left(1\right)=-2{\int }_0^{\mathrm{\infty }}\frac{\mathrm{lnx}}{{({\mathrm{x}}^2+1)}^2}\Rightarrow {\int }_0^{\mathrm{\infty }}\frac{\mathrm{lnx}}{{({\mathrm{x}}^2+1)}^2}=-\frac{1}{2}{\mathrm{f}}^{{}^{\prime }}\left(1\right)$$$$\mathrm{f}\left(\mathrm{a}\right){=}_{\mathrm{x}=\mathrm{at}}{\int }_0^{\mathrm{\infty }}\frac{\mathrm{lna}+\mathrm{lnt}}{{\mathrm{a}}^2(1+{\mathrm{t}}^2)}\mathrm{adt}=\frac{1}{\mathrm{a}}{\int }_0^{\mathrm{\infty }}\frac{\mathrm{lna}+\mathrm{lnt}}{(1+{\mathrm{t}}^2)}\mathrm{dt}$$$$=\frac{\mathrm{lna}}{\mathrm{a}}{\int }_0^{\mathrm{\infty }}\frac{\mathrm{dt}}{1+{\mathrm{t}}^2}+\frac{1}{\mathrm{a}}{\int }_0^{\mathrm{\infty }}\frac{\mathrm{lnt}}{1+{\mathrm{t}}^2}\mathrm{dt}\mathrm{but}{\int }_0^{\mathrm{\infty }}\frac{\mathrm{lnt}}{1+{\mathrm{t}}^2}\mathrm{dt}=0\left(\mathrm{proved}\right)\Rightarrow$$$$\mathrm{f}\left(\mathrm{a}\right)=\frac{\mathrm{lna}}{\mathrm{a}}.\frac{\pi }{2}=\frac{\pi \mathrm{lna}}{2\mathrm{a}}\Rightarrow {\mathrm{f}}^{{}^{\prime }}\left(\mathrm{a}\right)=\frac{\frac{\pi }{\mathrm{a}}\left(2\mathrm{a}\right)-2\pi \mathrm{lna}}{{4\mathrm{a}}^2}\Rightarrow {\mathrm{f}}^{{}^{\prime }}\left(1\right)=\frac{2\pi }{4}=\frac{\pi }{2}\Rightarrow$$$${\int }_0^{\mathrm{\infty }}\frac{\mathrm{lnx}}{{({\mathrm{x}}^2+1)}^2}\mathrm{dx}=-\frac{1}{2}.\frac{\pi }{2}=-\frac{\pi }{4}$$

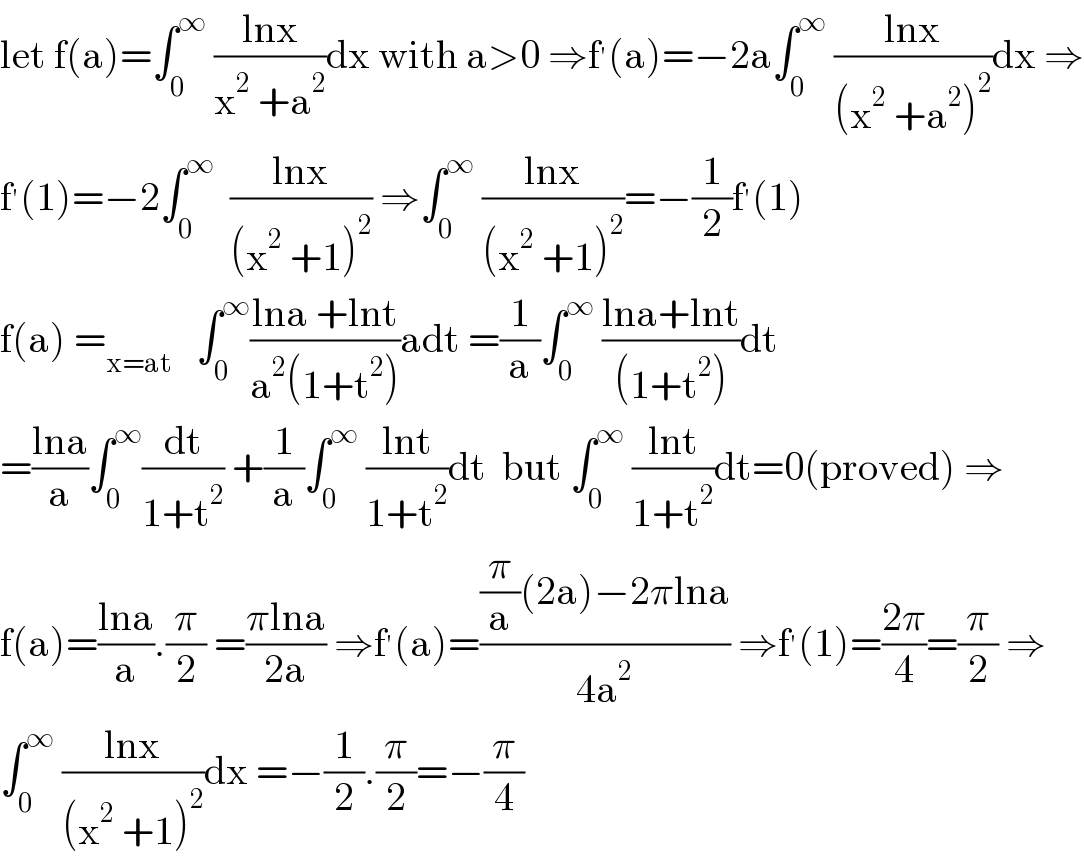
Commented by mathmax by abdo last updated on 19/Mar/21

$$\mathrm{folow}\mathrm{my}\mathrm{facebook}\left(\mathrm{abdo}\mathrm{imad}\right)$$

Commented by Ajetunmobi last updated on 19/Mar/21

$$$$$$\mathbf{sir}\mathbf{mathmax}\mathbf{by}\mathbf{abdo}$$$$\mathbf{how}\mathbf{can}\mathbf{we}\mathbf{chat}\mathbf{privately}\mathbf{sir}\mathbf{i}\mathbf{need}\mathbf{to}$$$$\mathbf{talk}\mathbf{about}\mathbf{something}\mathbf{with}\mathbf{you}$$$$\mathbf{you}\mathbf{can}\mathbf{send}\mathbf{me}\mathbf{your}\mathbf{whatsapp}\mathbf{number}$$$$\mathbf{or}\mathbf{your}\mathbf{facebook}\mathbf{name}$$$$\mathbf{Thanks}$$

Commented by Ajetunmobi last updated on 20/Mar/21

$$$$$$\mathbf{there}\mathbf{are}\mathbf{many}\mathbf{abdo}\mathbf{imad}\mathbf{there}$$$$\mathbf{how}\mathbf{will}\mathbf{i}\mathbf{recognize}\mathbf{you}\mathbf{sir}?$$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com