Question Number 13622 by Tinkutara last updated on 21/May/17
$$\mathrm{Evaluate}:\:\int_{\mathrm{0}} ^{\mathrm{2}\pi} {e}^{\frac{{x}}{\mathrm{2}}} \mathrm{sin}\:\left(\frac{{x}}{\mathrm{2}}\:+\:\frac{\pi}{\mathrm{4}}\right){dx} \\ $$
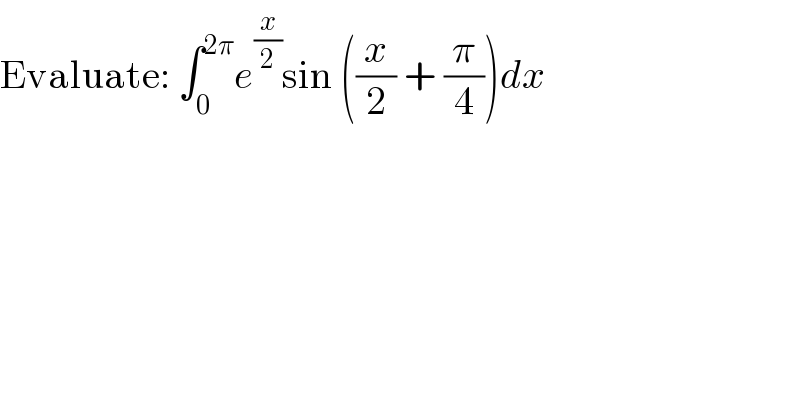
Answered by ajfour last updated on 22/May/17
![I=∫_0 ^( 2π) e^(x/2) sin ((x/2)+(π/4))dx (I/2)=∫_0 ^( 2π) e^(x/2) sin ((x/2)+(π/4))(dx/2) let t=(x/2) ⇒ dt=(dx/2) when x=0, t=0 ; and for x=2π, t=π (I/2)=∫_0 ^( π) e^t sin ((π/4)+t)dt =[e^t sin ((π/4)+t)]_0 ^π −∫_0 ^( π) e^t cos ((π/4)+t)dt =−(1/(√2))(e^π +1)−[e^t cos ((π/4)+t)]_0 ^π +∫_0 ^( π) e^t sin ((π/4)+t)dt ⇒ (I/2)=−(1/(√2))(e^π +1)+(1/(√2))(e^π +1)+I ⇒ I=0 .](Q13625.png)
$${I}=\int_{\mathrm{0}} ^{\:\:\mathrm{2}\pi} {e}^{\boldsymbol{{x}}/\mathrm{2}} \mathrm{sin}\:\left(\frac{{x}}{\mathrm{2}}+\frac{\pi}{\mathrm{4}}\right){dx} \\ $$$$\frac{{I}}{\mathrm{2}}=\int_{\mathrm{0}} ^{\:\:\mathrm{2}\pi} {e}^{\boldsymbol{{x}}/\mathrm{2}} \mathrm{sin}\:\left(\frac{{x}}{\mathrm{2}}+\frac{\pi}{\mathrm{4}}\right)\frac{{dx}}{\mathrm{2}} \\ $$$${let}\:\:{t}=\frac{{x}}{\mathrm{2}}\:\:\:\Rightarrow\:\:{dt}=\frac{{dx}}{\mathrm{2}} \\ $$$${when}\:{x}=\mathrm{0},\:{t}=\mathrm{0}\:;\: \\ $$$${and}\:{for}\:{x}=\mathrm{2}\pi,\:{t}=\pi \\ $$$$\frac{{I}}{\mathrm{2}}=\int_{\mathrm{0}} ^{\:\:\pi} {e}^{{t}} \mathrm{sin}\:\left(\frac{\pi}{\mathrm{4}}+{t}\right){dt} \\ $$$$\:\:=\left[{e}^{{t}} \mathrm{sin}\:\left(\frac{\pi}{\mathrm{4}}+{t}\right)\right]_{\mathrm{0}} ^{\pi} −\int_{\mathrm{0}} ^{\:\:\pi} {e}^{{t}} \mathrm{cos}\:\left(\frac{\pi}{\mathrm{4}}+{t}\right){dt} \\ $$$$\:\:=−\frac{\mathrm{1}}{\sqrt{\mathrm{2}}}\left({e}^{\pi} +\mathrm{1}\right)−\left[{e}^{{t}} \mathrm{cos}\:\left(\frac{\pi}{\mathrm{4}}+{t}\right)\right]_{\mathrm{0}} ^{\pi} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:+\int_{\mathrm{0}} ^{\:\:\pi} {e}^{{t}} \mathrm{sin}\:\left(\frac{\pi}{\mathrm{4}}+{t}\right){dt} \\ $$$$\Rightarrow\:\frac{{I}}{\mathrm{2}}=−\frac{\mathrm{1}}{\sqrt{\mathrm{2}}}\left({e}^{\pi} +\mathrm{1}\right)+\frac{\mathrm{1}}{\sqrt{\mathrm{2}}}\left({e}^{\pi} +\mathrm{1}\right)+{I} \\ $$$$\Rightarrow\:\:\boldsymbol{{I}}=\mathrm{0}\:. \\ $$
Commented by ajfour last updated on 22/May/17
$${cannot}\:{you}\:{confirm}\:{the}\:{answer}.. \\ $$
Commented by Tinkutara last updated on 22/May/17
$$\mathrm{Answer}\:\mathrm{given}\:\mathrm{is}\:\mathrm{0}. \\ $$
Commented by ajfour last updated on 22/May/17
$${thanks},\:{notice}\:{the}\:{difference}\:! \\ $$