Question and Answers Forum

All Questions      Topic List

Others Questions

Previous in All Question      Next in All Question      

Previous in Others      Next in Others      

Question Number 136420 by Dwaipayan Shikari last updated on 21/Mar/21

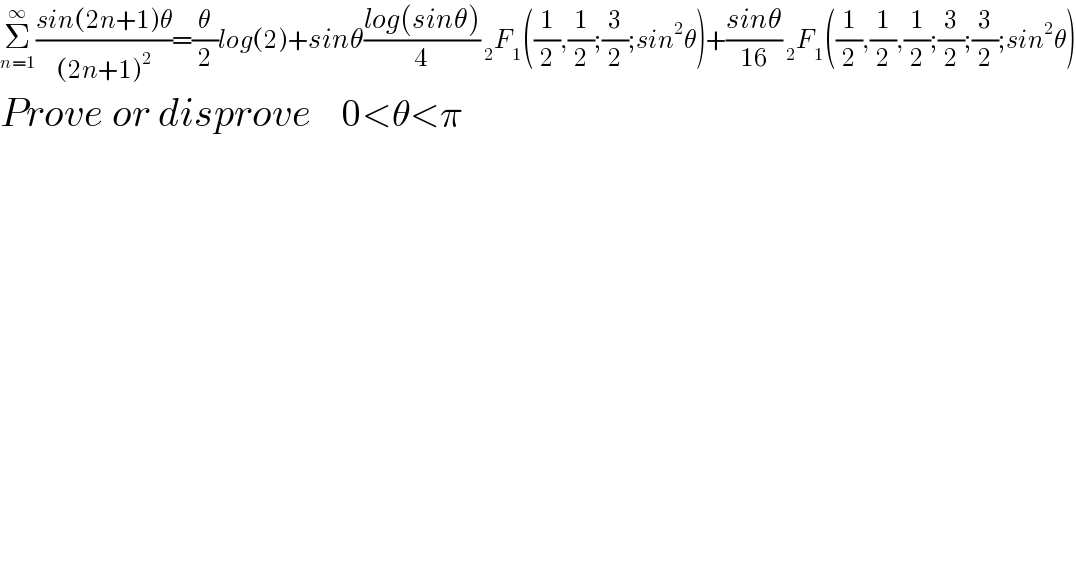
Σ_(n=1) ^∞ ((sin(2n+1)θ)/((2n+1)^2 ))=(θ/2)log(2)+sinθ((log(sinθ))/4) _2 F_1 ((1/2),(1/2);(3/2);sin^2 θ)+((sinθ)/(16)) _2 F_1 ((1/2),(1/2),(1/2);(3/2);(3/2);sin^2 θ) Prove or disprove 0<θ<π

$$\underset{{n}=\mathrm{1}} {\overset{\infty} {\sum}}\frac{{sin}\left(\mathrm{2}{n}+\mathrm{1}\right)\theta}{\left(\mathrm{2}{n}+\mathrm{1}\right)^{\mathrm{2}} }=\frac{\theta}{\mathrm{2}}{log}\left(\mathrm{2}\right)+{sin}\theta\frac{{log}\left({sin}\theta\right)}{\mathrm{4}}\:_{\mathrm{2}} {F}_{\mathrm{1}} \left(\frac{\mathrm{1}}{\mathrm{2}},\frac{\mathrm{1}}{\mathrm{2}};\frac{\mathrm{3}}{\mathrm{2}};{sin}^{\mathrm{2}} \theta\right)+\frac{{sin}\theta}{\mathrm{16}}\:_{\mathrm{2}} {F}_{\mathrm{1}} \left(\frac{\mathrm{1}}{\mathrm{2}},\frac{\mathrm{1}}{\mathrm{2}},\frac{\mathrm{1}}{\mathrm{2}};\frac{\mathrm{3}}{\mathrm{2}};\frac{\mathrm{3}}{\mathrm{2}};{sin}^{\mathrm{2}} \theta\right) \\ $$ $${Prove}\:{or}\:{disprove}\:\:\:\:\:\mathrm{0}<\theta<\pi \\ $$

Answered by mindispower last updated on 21/Mar/21

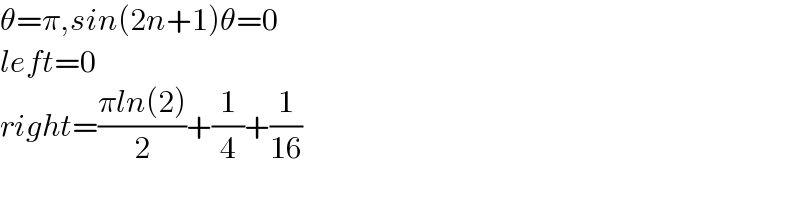
θ=π,sin(2n+1)θ=0 left=0 right=((πln(2))/2)+(1/4)+(1/(16))

$$\theta=\pi,{sin}\left(\mathrm{2}{n}+\mathrm{1}\right)\theta=\mathrm{0} \\ $$ $${left}=\mathrm{0} \\ $$ $${right}=\frac{\pi{ln}\left(\mathrm{2}\right)}{\mathrm{2}}+\frac{\mathrm{1}}{\mathrm{4}}+\frac{\mathrm{1}}{\mathrm{16}} \\ $$

Commented byDwaipayan Shikari last updated on 21/Mar/21

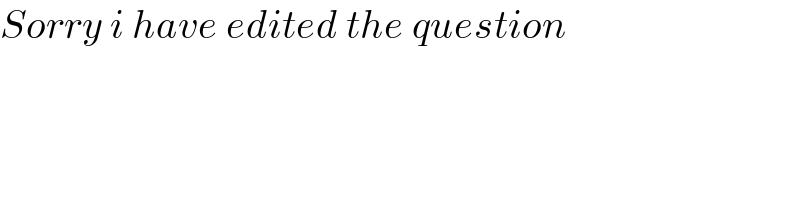
Sorry i have edited the question

$${Sorry}\:{i}\:{have}\:{edited}\:{the}\:{question} \\ $$

Commented byDwaipayan Shikari last updated on 21/Mar/21

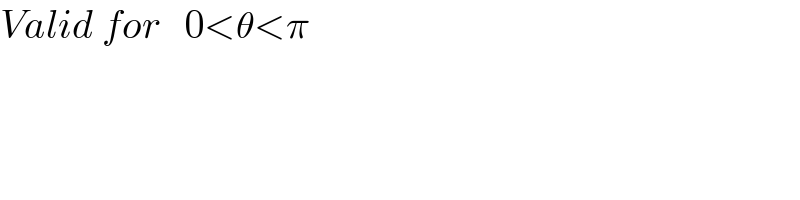
Valid for 0<θ<π

$${Valid}\:{for}\:\:\:\mathrm{0}<\theta<\pi \\ $$

Commented bymindispower last updated on 22/Mar/21

ok i will try but tchek it again

$${ok}\:{i}\:{will}\:{try}\:{but}\:\:{tchek}\:{it}\:{again} \\ $$

Answered by mindispower last updated on 22/Mar/21

Σ_(n≥0) ((sin(2n+1)θ)/((2n+1)^2 ))∫=S=Σ_(n≥1) ((sin(nθ))/n^2 )−Σ_(n≥1) ((sin(2θ))/(4n^2 )) recal Σ_(n≥1) ((sin(nθ))/n^2 )=Cl_2 (θ),clausen function we get S=Cl_2 (θ)−((Cl_2 (2θ))/4) clausen integration representation Cl_2 (θ)=−2∫_0 ^(θ/2) ln(2sin(t))dt =u=sin(t)=−2∫_0 ^(sin((θ/2))) ((ln(2u))/( (√(1−u^2 ))))du=cl_2 (θ) (1+x)^a =1+Σ_(n≥1) ((Π_(k≤n−1) (a−k))/(n!)).x^n cl_2 (θ)=−2∫_0 ^(sin((θ/2))) (1+Σ_(n≥1) (−1)^n ((Π_(k≤n−1) (−(1/2)−k)u^(2n) )/(n!)))ln(2u)du ∫u^(2n) ln(2u)du=(u^(2n+1) /(2n+1))ln(2u)−(u^(2n+1) /((2n+1)^2 )) it seems good starte we can fin _p F_q sinlog(sin..) also i think verry long worck =−2(1+Σ_(n≥1) ((((1/2))_n )/(n!)))(((sin^(2n+1) ((θ/2))ln(2sin((θ/2))))/((2n+1)))−((sin^(2n+1) ((θ/2)))/((2n+1)^2 ))) =−2(1+Σ_(n≥1) ((((1/2))_n ((1/2))_n )/(2.((3/2))_n ))

$$\underset{{n}\geqslant\mathrm{0}} {\sum}\frac{{sin}\left(\mathrm{2}{n}+\mathrm{1}\right)\theta}{\left(\mathrm{2}{n}+\mathrm{1}\right)^{\mathrm{2}} }\int={S}=\underset{{n}\geqslant\mathrm{1}} {\sum}\frac{{sin}\left({n}\theta\right)}{{n}^{\mathrm{2}} }−\underset{{n}\geqslant\mathrm{1}} {\sum}\frac{{sin}\left(\mathrm{2}\theta\right)}{\mathrm{4}{n}^{\mathrm{2}} } \\ $$ $${recal}\:\underset{{n}\geqslant\mathrm{1}} {\sum}\frac{{sin}\left({n}\theta\right)}{{n}^{\mathrm{2}} }={Cl}_{\mathrm{2}} \left(\theta\right),{clausen}\:{function} \\ $$ $${we}\:{get}\:{S}={Cl}_{\mathrm{2}} \left(\theta\right)−\frac{{Cl}_{\mathrm{2}} \left(\mathrm{2}\theta\right)}{\mathrm{4}} \\ $$ $${clausen}\:{integration}\:\:{representation} \\ $$ $${Cl}_{\mathrm{2}} \left(\theta\right)=−\mathrm{2}\int_{\mathrm{0}} ^{\frac{\theta}{\mathrm{2}}} {ln}\left(\mathrm{2}{sin}\left({t}\right)\right){dt} \\ $$ $$={u}={sin}\left({t}\right)=−\mathrm{2}\int_{\mathrm{0}} ^{{sin}\left(\frac{\theta}{\mathrm{2}}\right)} \frac{{ln}\left(\mathrm{2}{u}\right)}{\:\sqrt{\mathrm{1}−{u}^{\mathrm{2}} }}{du}={cl}_{\mathrm{2}} \left(\theta\right) \\ $$ $$\left(\mathrm{1}+{x}\right)^{{a}} =\mathrm{1}+\underset{{n}\geqslant\mathrm{1}} {\sum}\frac{\underset{{k}\leqslant{n}−\mathrm{1}} {\prod}\left({a}−{k}\right)}{{n}!}.{x}^{{n}} \\ $$ $${cl}_{\mathrm{2}} \left(\theta\right)=−\mathrm{2}\int_{\mathrm{0}} ^{{sin}\left(\frac{\theta}{\mathrm{2}}\right)} \left(\mathrm{1}+\underset{{n}\geqslant\mathrm{1}} {\sum}\left(−\mathrm{1}\right)^{{n}} \frac{\underset{{k}\leqslant{n}−\mathrm{1}} {\prod}\left(−\frac{\mathrm{1}}{\mathrm{2}}−{k}\right){u}^{\mathrm{2}{n}} }{{n}!}\right){ln}\left(\mathrm{2}{u}\right){du} \\ $$ $$\int{u}^{\mathrm{2}{n}} {ln}\left(\mathrm{2}{u}\right){du}=\frac{{u}^{\mathrm{2}{n}+\mathrm{1}} }{\mathrm{2}{n}+\mathrm{1}}{ln}\left(\mathrm{2}{u}\right)−\frac{{u}^{\mathrm{2}{n}+\mathrm{1}} }{\left(\mathrm{2}{n}+\mathrm{1}\right)^{\mathrm{2}} } \\ $$ $${it}\:{seems}\:{good}\:{starte}\:{we}\:{can}\:{fin}\:_{{p}} {F}_{{q}} \:\: \\ $$ $${sinlog}\left({sin}..\right)\:{also}\:{i}\:{think}\:{verry}\:{long}\:{worck} \\ $$ $$=−\mathrm{2}\left(\mathrm{1}+\underset{{n}\geqslant\mathrm{1}} {\sum}\frac{\left(\frac{\mathrm{1}}{\mathrm{2}}\right)_{{n}} }{{n}!}\right)\left(\frac{{sin}^{\mathrm{2}{n}+\mathrm{1}} \left(\frac{\theta}{\mathrm{2}}\right){ln}\left(\mathrm{2}{sin}\left(\frac{\theta}{\mathrm{2}}\right)\right)}{\left(\mathrm{2}{n}+\mathrm{1}\right)}−\frac{{sin}^{\mathrm{2}{n}+\mathrm{1}} \left(\frac{\theta}{\mathrm{2}}\right)}{\left(\mathrm{2}{n}+\mathrm{1}\right)^{\mathrm{2}} }\right) \\ $$ $$=−\mathrm{2}\left(\mathrm{1}+\underset{{n}\geqslant\mathrm{1}} {\sum}\frac{\left(\frac{\mathrm{1}}{\mathrm{2}}\right)_{{n}} \left(\frac{\mathrm{1}}{\mathrm{2}}\right)_{{n}} }{\mathrm{2}.\left(\frac{\mathrm{3}}{\mathrm{2}}\right)_{{n}} }\right. \\ $$

Commented byDwaipayan Shikari last updated on 22/Mar/21

Thanks sir! I will post my work later

$${Thanks}\:{sir}!\:{I}\:{will}\:{post}\:{my}\:{work}\:{later} \\ $$

Commented bymindispower last updated on 22/Mar/21

you are welcom

$${you}\:{are}\:{welcom} \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com