Question Number 136497 by mnjuly1970 last updated on 22/Mar/21
$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:......{nice}\:\:\:\:{calculus}..... \\ $$$$\:\:\:\:{prove}::\:\: \\ $$$$\:\:\:\:\:\:\:\int_{\mathrm{0}} ^{\:\mathrm{1}} \frac{\mathrm{1}}{\mathrm{1}+{ln}^{\mathrm{2}} \left({x}\right)}{dx}=\int_{\mathrm{0}\:} ^{\:\infty} \frac{{sin}\left({x}\right)}{\mathrm{1}+{x}}{dx} \\ $$$$ \\ $$
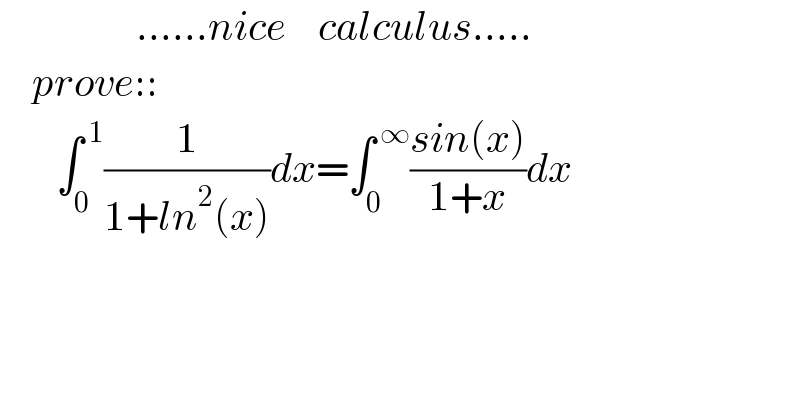
Commented by Dwaipayan Shikari last updated on 22/Mar/21
$$\int_{\mathrm{0}} ^{\infty} \frac{{sin}\left({x}\right)}{\mathrm{1}+{x}}{dx} \\ $$$$=\int_{\mathrm{0}} ^{\infty} \int_{\mathrm{0}} ^{\infty} {e}^{−\left({x}+\mathrm{1}\right){t}} {sin}\left({x}\right){dtdx} \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}{i}}\int_{\mathrm{0}} ^{\infty} \int_{\mathrm{0}} ^{\infty} {e}^{−{t}} {e}^{−\left({t}−{i}\right){x}} −{e}^{−{t}} {e}^{−\left({t}+{i}\right){x}} {dxdt} \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}{i}}\int_{\mathrm{0}} ^{\infty} \frac{{e}^{−{t}} }{{t}−{i}}−\frac{{e}^{−{t}} }{{t}+{i}}{dt} \\ $$$$=\int_{\mathrm{0}} ^{\infty} \frac{{e}^{−{t}} }{{t}^{\mathrm{2}} +\mathrm{1}}{dt}\:\:\:\:\:\:\:\:\:−{t}={log}\left({u}\right)\Rightarrow\mathrm{1}=−\frac{\mathrm{1}}{{u}}.\frac{{du}}{{dt}} \\ $$$$=\int_{\mathrm{0}} ^{\mathrm{1}} \frac{\mathrm{1}}{\mathrm{1}+{log}^{\mathrm{2}} \left({u}\right)}{du} \\ $$
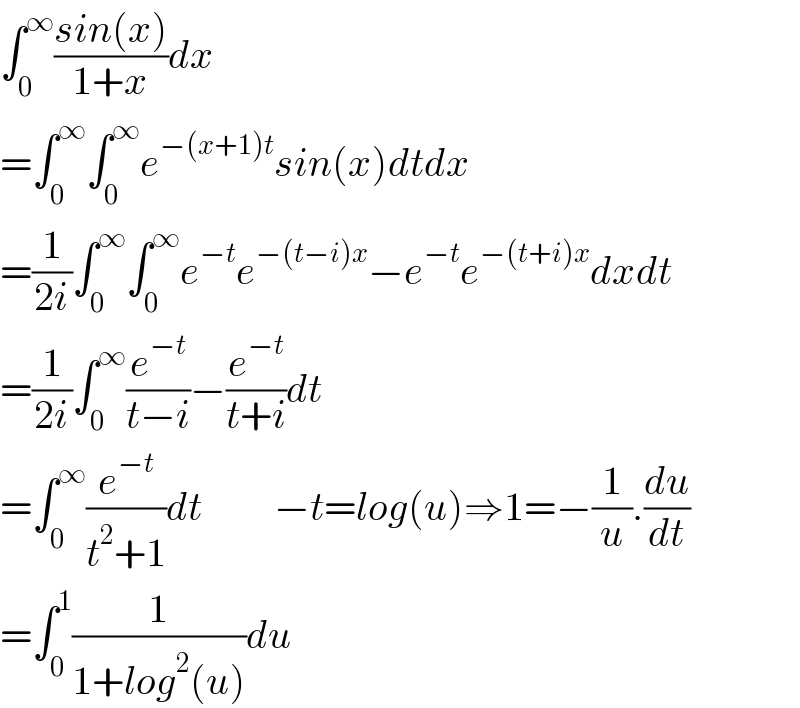
Commented by mnjuly1970 last updated on 22/Mar/21
$$\:{grateful}\:{mr}\:{payan}... \\ $$
Answered by mindispower last updated on 22/Mar/21
![t=−ln(x) =∫_0 ^∞ (e^(−t) /(1+t^2 ))dt=∫_0 ^∞ (((t+i)−(t−i))/(2i(t+i)(t−i)))e^(−t) =(1/(2i))(∫_0 ^∞ (e^(−t) /(t−i))dt−∫_0 ^∞ (e^(−t) /(t+i))) =Im ∫_0 ^∞ (e^(−t) /(t−i))dt let z=it =Im ∫_0 ^(i∞) (e^(iz) /(i(t+1))).(dz/i)=Im(−∫_0 ^(i∞) (e^(iz) /(t+1))dz)...2 let C_R =[0,R]∪(Re^(iθ) ,θ∈[0,(π/2)])_D ∪[iR,0] ∫_C_R (e^(iz) /(z+1))dz=0..1,z→(e^(iz) /(z+1)) holomorphic without pols over C_R ∫_D (e^(iz) /(z+1))=0⇒..2 (1)&(2)⇒ ∫_0 ^∞ (e^(iz) /(z+1))dz=−∫_0 ^(i∞) (e^(iz) /(z+1))dz we get Im ∫_0 ^∞ (e^(iz) /(z+1))dz=∫_0 ^∞ ((sin(z))/(z+1))dz](Q136508.png)
$${t}=−{ln}\left({x}\right) \\ $$$$=\int_{\mathrm{0}} ^{\infty} \frac{{e}^{−{t}} }{\mathrm{1}+{t}^{\mathrm{2}} }{dt}=\int_{\mathrm{0}} ^{\infty} \frac{\left({t}+{i}\right)−\left({t}−{i}\right)}{\mathrm{2}{i}\left({t}+{i}\right)\left({t}−{i}\right)}{e}^{−{t}} \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}{i}}\left(\int_{\mathrm{0}} ^{\infty} \frac{{e}^{−{t}} }{{t}−{i}}{dt}−\int_{\mathrm{0}} ^{\infty} \frac{{e}^{−{t}} }{{t}+{i}}\right) \\ $$$$={Im}\:\int_{\mathrm{0}} ^{\infty} \frac{{e}^{−{t}} }{{t}−{i}}{dt} \\ $$$${let}\:{z}={it} \\ $$$$={Im}\:\int_{\mathrm{0}} ^{{i}\infty} \frac{{e}^{{iz}} }{{i}\left({t}+\mathrm{1}\right)}.\frac{{dz}}{{i}}={Im}\left(−\int_{\mathrm{0}} ^{{i}\infty} \frac{{e}^{{iz}} }{{t}+\mathrm{1}}{dz}\right)...\mathrm{2} \\ $$$${let}\:{C}_{{R}} =\left[\mathrm{0},{R}\right]\cup\left({Re}^{{i}\theta} ,\theta\in\left[\mathrm{0},\frac{\pi}{\mathrm{2}}\right]\right)_{{D}} \cup\left[{iR},\mathrm{0}\right] \\ $$$$\int_{{C}_{{R}} } \frac{{e}^{{iz}} }{{z}+\mathrm{1}}{dz}=\mathrm{0}..\mathrm{1},{z}\rightarrow\frac{{e}^{{iz}} }{{z}+\mathrm{1}}\:{holomorphic}\:{without}\:{pols} \\ $$$${over}\:{C}_{{R}} \\ $$$$\int_{{D}} \frac{{e}^{{iz}} }{{z}+\mathrm{1}}=\mathrm{0}\Rightarrow..\mathrm{2}\:\:\left(\mathrm{1}\right)\&\left(\mathrm{2}\right)\Rightarrow \\ $$$$\int_{\mathrm{0}} ^{\infty} \frac{{e}^{{iz}} }{{z}+\mathrm{1}}{dz}=−\int_{\mathrm{0}} ^{{i}\infty} \frac{{e}^{{iz}} }{{z}+\mathrm{1}}{dz} \\ $$$${we}\:{get}\:{Im}\:\int_{\mathrm{0}} ^{\infty} \frac{{e}^{{iz}} }{{z}+\mathrm{1}}{dz}=\int_{\mathrm{0}} ^{\infty} \frac{{sin}\left({z}\right)}{{z}+\mathrm{1}}{dz} \\ $$$$ \\ $$$$ \\ $$$$ \\ $$
Commented by mnjuly1970 last updated on 22/Mar/21
$${thank}\:{you}\:{so}\:{much}\:{mr}\:{power}... \\ $$
Commented by mindispower last updated on 22/Mar/21
$${pleasur} \\ $$