Question and Answers Forum

All Questions      Topic List

None Questions

Previous in All Question      Next in All Question      

Previous in None      Next in None      

Question Number 136559 by mohammad17 last updated on 23/Mar/21

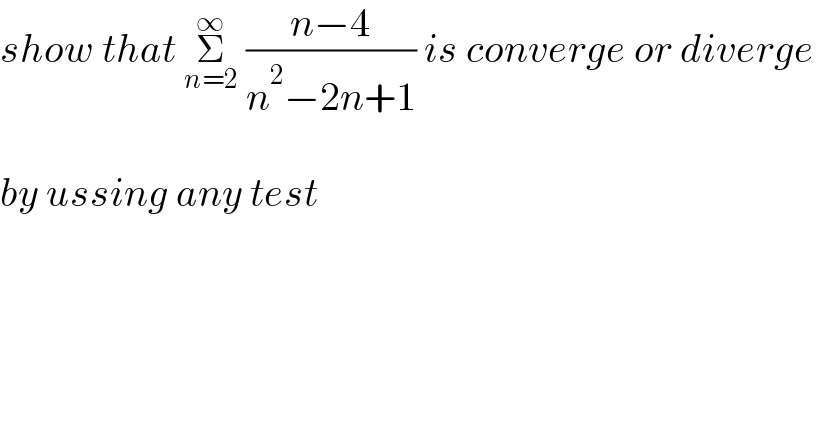
show that Σ_(n=2) ^∞ ((n−4)/(n^2 −2n+1)) is converge or diverge by ussing any test

$${show}\:{that}\:\underset{{n}=\mathrm{2}} {\overset{\infty} {\sum}}\:\frac{{n}−\mathrm{4}}{{n}^{\mathrm{2}} −\mathrm{2}{n}+\mathrm{1}}\:{is}\:{converge}\:{or}\:{diverge}\: \\ $$$$ \\ $$$${by}\:{ussing}\:{any}\:{test} \\ $$

Commented by mr W last updated on 23/Mar/21

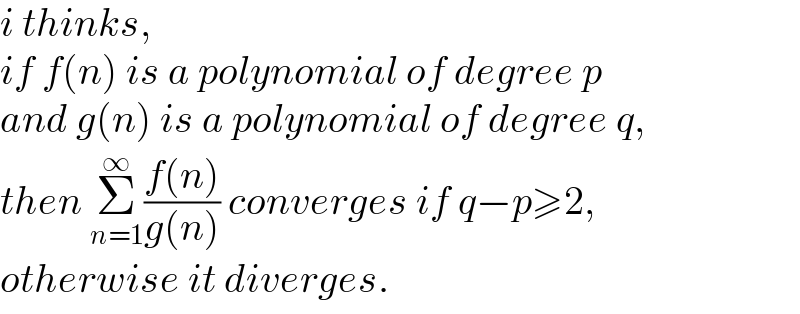
i thinks, if f(n) is a polynomial of degree p and g(n) is a polynomial of degree q, then Σ_(n=1) ^∞ ((f(n))/(g(n))) converges if q−p≥2, otherwise it diverges.

$${i}\:{thinks}, \\ $$$${if}\:{f}\left({n}\right)\:{is}\:{a}\:{polynomial}\:{of}\:{degree}\:{p} \\ $$$${and}\:{g}\left({n}\right)\:{is}\:{a}\:{polynomial}\:{of}\:{degree}\:{q}, \\ $$$${then}\:\underset{{n}=\mathrm{1}} {\overset{\infty} {\sum}}\frac{{f}\left({n}\right)}{{g}\left({n}\right)}\:{converges}\:{if}\:{q}−{p}\geqslant\mathrm{2},\: \\ $$$${otherwise}\:{it}\:{diverges}. \\ $$

Answered by physicstutes last updated on 23/Mar/21

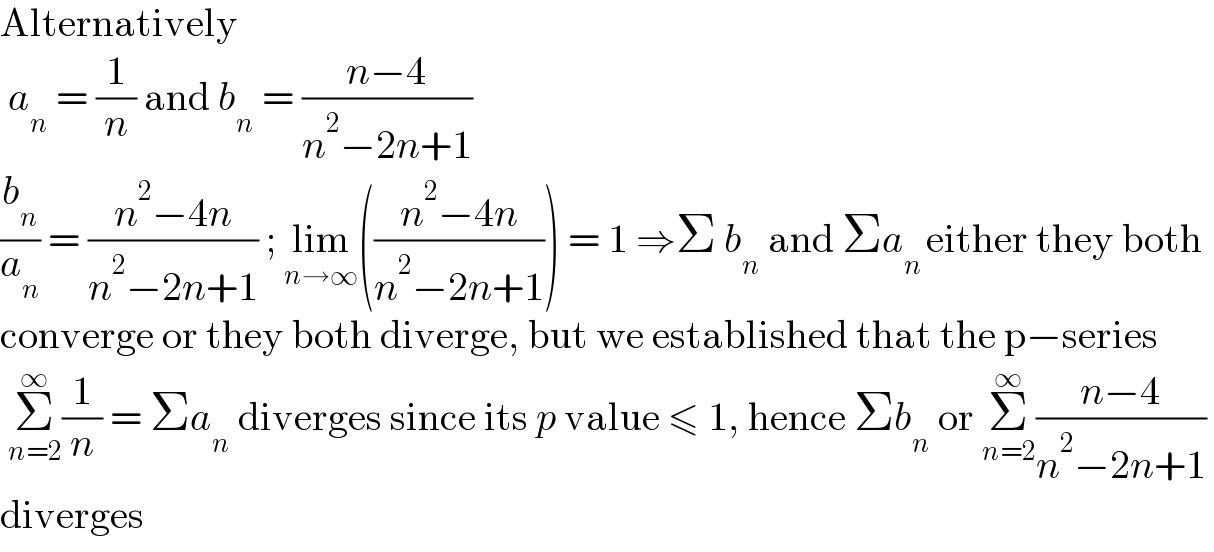
Alternatively a_n = (1/n) and b_n = ((n−4)/(n^2 −2n+1)) (b_n /a_n ) = ((n^2 −4n)/(n^2 −2n+1)) ; lim_(n→∞) (((n^2 −4n)/(n^2 −2n+1))) = 1 ⇒Σ b_n and Σa_(n ) either they both converge or they both diverge, but we established that the p−series Σ_(n=2) ^∞ (1/n) = Σa_n diverges since its p value ≤ 1, hence Σb_n or Σ_(n=2) ^∞ ((n−4)/(n^2 −2n+1)) diverges

$$\mathrm{Alternatively} \\ $$$$\:{a}_{{n}} \:=\:\frac{\mathrm{1}}{{n}}\:\mathrm{and}\:{b}_{{n}} \:=\:\frac{{n}−\mathrm{4}}{{n}^{\mathrm{2}} −\mathrm{2}{n}+\mathrm{1}} \\ $$$$\frac{{b}_{{n}} }{{a}_{{n}} }\:=\:\frac{{n}^{\mathrm{2}} −\mathrm{4}{n}}{{n}^{\mathrm{2}} −\mathrm{2}{n}+\mathrm{1}}\:;\:\underset{{n}\rightarrow\infty} {\mathrm{lim}}\left(\frac{{n}^{\mathrm{2}} −\mathrm{4}{n}}{{n}^{\mathrm{2}} −\mathrm{2}{n}+\mathrm{1}}\right)\:=\:\mathrm{1}\:\Rightarrow\Sigma\:{b}_{{n}} \:\mathrm{and}\:\Sigma{a}_{{n}\:} \mathrm{either}\:\mathrm{they}\:\mathrm{both} \\ $$$$\mathrm{converge}\:\mathrm{or}\:\mathrm{they}\:\mathrm{both}\:\mathrm{diverge},\:\mathrm{but}\:\mathrm{we}\:\mathrm{established}\:\mathrm{that}\:\mathrm{the}\:\mathrm{p}−\mathrm{series} \\ $$$$\:\underset{{n}=\mathrm{2}} {\overset{\infty} {\sum}}\frac{\mathrm{1}}{{n}}\:=\:\Sigma{a}_{{n}} \:\mathrm{diverges}\:\mathrm{since}\:\mathrm{its}\:{p}\:\mathrm{value}\:\leqslant\:\mathrm{1},\:\mathrm{hence}\:\Sigma{b}_{{n}} \:\mathrm{or}\:\underset{{n}=\mathrm{2}} {\overset{\infty} {\sum}}\frac{{n}−\mathrm{4}}{{n}^{\mathrm{2}} −\mathrm{2}{n}+\mathrm{1}}\: \\ $$$$\mathrm{diverges} \\ $$

Answered by Olaf last updated on 23/Mar/21

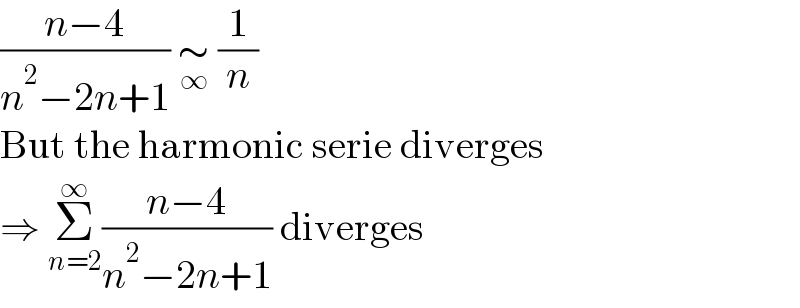
((n−4)/(n^2 −2n+1)) ∼_∞ (1/n) But the harmonic serie diverges ⇒ Σ_(n=2) ^∞ ((n−4)/(n^2 −2n+1)) diverges

$$\frac{{n}−\mathrm{4}}{{n}^{\mathrm{2}} −\mathrm{2}{n}+\mathrm{1}}\:\underset{\infty} {\sim}\:\frac{\mathrm{1}}{{n}} \\ $$$$\mathrm{But}\:\mathrm{the}\:\mathrm{harmonic}\:\mathrm{serie}\:\mathrm{diverges} \\ $$$$\Rightarrow\:\underset{{n}=\mathrm{2}} {\overset{\infty} {\sum}}\frac{{n}−\mathrm{4}}{{n}^{\mathrm{2}} −\mathrm{2}{n}+\mathrm{1}}\:\mathrm{diverges} \\ $$

Answered by physicstutes last updated on 23/Mar/21

when n→∞ we can get a comparison series of Σ_(n=2) ^∞ (1/n) which is divergnt let b_n = ((n−4)/(n^2 −2n+1)) and a_n = (1/n) since Σa_n diverges, ⇒ Σb_n diverges by the comparison test

$$\mathrm{when}\:{n}\rightarrow\infty\:\mathrm{we}\:\mathrm{can}\:\mathrm{get}\:\mathrm{a}\:\mathrm{comparison}\:\mathrm{series}\:\mathrm{of}\:\underset{{n}=\mathrm{2}} {\overset{\infty} {\sum}}\frac{\mathrm{1}}{{n}}\:\mathrm{which}\:\mathrm{is}\:\mathrm{divergnt} \\ $$$$\:\mathrm{let}\:{b}_{{n}} \:=\:\frac{{n}−\mathrm{4}}{{n}^{\mathrm{2}} −\mathrm{2}{n}+\mathrm{1}}\:\mathrm{and}\:{a}_{{n}} \:=\:\frac{\mathrm{1}}{{n}} \\ $$$$\mathrm{since}\:\Sigma{a}_{{n}} \:\mathrm{diverges},\:\Rightarrow\:\Sigma{b}_{{n}} \:\mathrm{diverges}\:\mathrm{by}\:\mathrm{the}\:\mathrm{comparison}\:\mathrm{test} \\ $$

Answered by physicstutes last updated on 23/Mar/21

another alternative Σ_(n=2) ^∞ (((n−4)/(n^2 −2n+1))) = Σ_(n=2) ^∞ [((n−4)/((n−1)^2 ))] = Σ_(n=2) ^∞ ((1/(n−1))−(3/((n−1)^2 ))) Σ_(n=2) ^∞ ((1/(n−1))) another divergent harmonic Σ_(n=2) ^∞ [(3/((n−1)^2 ))] yet another divergent one so Σ_(n=2) ^∞ (((n−4)/(n^2 −2n+1))) is divergent from all universes.

$$\mathrm{another}\:\mathrm{alternative} \\ $$$$\:\underset{{n}=\mathrm{2}} {\overset{\infty} {\sum}}\left(\frac{{n}−\mathrm{4}}{{n}^{\mathrm{2}} −\mathrm{2}{n}+\mathrm{1}}\right)\:=\:\underset{{n}=\mathrm{2}} {\overset{\infty} {\sum}}\:\left[\frac{{n}−\mathrm{4}}{\left({n}−\mathrm{1}\right)^{\mathrm{2}} }\right]\:=\:\underset{{n}=\mathrm{2}} {\overset{\infty} {\sum}}\left(\frac{\mathrm{1}}{{n}−\mathrm{1}}−\frac{\mathrm{3}}{\left({n}−\mathrm{1}\right)^{\mathrm{2}} }\right) \\ $$$$\underset{{n}=\mathrm{2}} {\overset{\infty} {\sum}}\left(\frac{\mathrm{1}}{{n}−\mathrm{1}}\right)\:\mathrm{another}\:\mathrm{divergent}\:\mathrm{harmonic} \\ $$$$\:\underset{{n}=\mathrm{2}} {\overset{\infty} {\sum}}\left[\frac{\mathrm{3}}{\left({n}−\mathrm{1}\right)^{\mathrm{2}} }\right]\:\mathrm{yet}\:\mathrm{another}\:\mathrm{divergent}\:\mathrm{one}\:\mathrm{so}\:\underset{{n}=\mathrm{2}} {\overset{\infty} {\sum}}\left(\frac{{n}−\mathrm{4}}{{n}^{\mathrm{2}} −\mathrm{2}{n}+\mathrm{1}}\right)\:\mathrm{is}\:\mathrm{divergent} \\ $$$$\mathrm{from}\:\mathrm{all}\:\mathrm{universes}. \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com