
Question and Answers Forum
Question Number 136943 by Mathspace last updated on 28/Mar/21
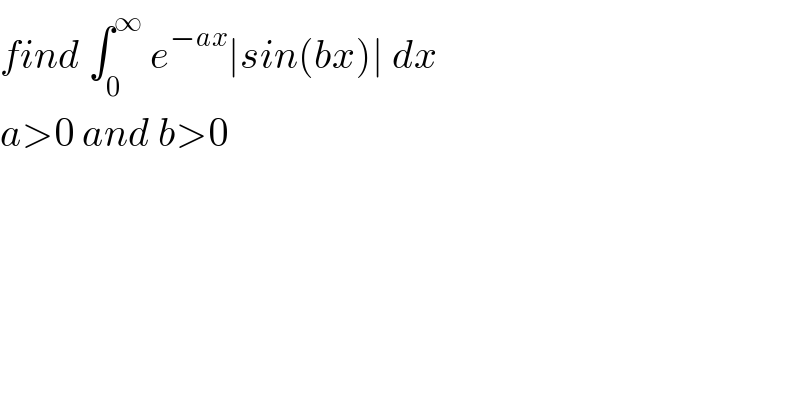
Answered by mathmax by abdo last updated on 30/Mar/21
![Φ=∫_0 ^∞ e^(−ax) ∣sin(bx)∣dx ⇒Φ=_(bx=t) ∫_0 ^∞ e^(−(a/b)t) ∣sint∣(dt/b) =(1/b) Σ_(n=0) ^∞ ∫_(nπ) ^((n+1)π) e^(−((at)/b)) ∣sint∣ dt =_(t=nπ +y) (1/b)Σ_(n=0) ^∞ ∫^π _0 e^(−(a/b)(nπ+y)) ∣sin(nπ+y)∣ dy =(1/b)Σ_(n=0) ^∞ e^(−((naπ)/b)) ∫_0 ^π e^(−((ay)/b)) siny dy let (a/b)=λ ⇒ Φ=(1/b) Σ_(n=0) ^∞ e^(−nλπ) .∫_0 ^π e^(−λy) siny dy we have ∫_0 ^π e^(−λy) siny dy =Im(∫_0 ^π e^(−λy+iy) dy) and ∫_0 ^π e^((−λ+i)y) dy =[(1/(−λ+i))e^((−λ+i)y) ]_0 ^π =((−1)/(λ−i)){e^((−λ+i)π) −1} =((−(λ+i))/(1+λ^2 )){− e^(−λπ) −1} =(((λ+i)(e^(−λπ) +1))/(1+λ^2 )) ⇒∫_0 ^π e^(−λy) siny dy =((1+e^(−λπ) )/(1+λ^2 )) ⇒ Φ =((1+e^(−λπ) )/(b(1+λ^2 )))Σ_(n=0) ^∞ (e^(−λπ) )^n =((1+e^(−λπ) )/(b(1+λ^2 )))×(1/(1−e^(−λπ) )) ⇒ Φ =((1+e^(−((aπ)/b)) )/(b(1−e^(−((aπ)/b)) )(1+(a^2 /b^2 )))) ⇒Φ=(b/(a^2 +b^2 ))×((1+e^(−((aπ)/b)) )/(1−e^(−((aπ)/b)) ))](Q137122.png)
| ||
Question and Answers Forum | ||
Question Number 136943 by Mathspace last updated on 28/Mar/21 | ||
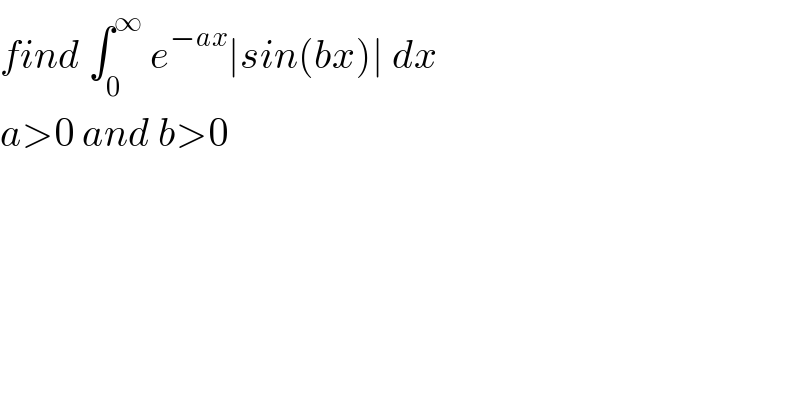 | ||
Answered by mathmax by abdo last updated on 30/Mar/21 | ||
![Φ=∫_0 ^∞ e^(−ax) ∣sin(bx)∣dx ⇒Φ=_(bx=t) ∫_0 ^∞ e^(−(a/b)t) ∣sint∣(dt/b) =(1/b) Σ_(n=0) ^∞ ∫_(nπ) ^((n+1)π) e^(−((at)/b)) ∣sint∣ dt =_(t=nπ +y) (1/b)Σ_(n=0) ^∞ ∫^π _0 e^(−(a/b)(nπ+y)) ∣sin(nπ+y)∣ dy =(1/b)Σ_(n=0) ^∞ e^(−((naπ)/b)) ∫_0 ^π e^(−((ay)/b)) siny dy let (a/b)=λ ⇒ Φ=(1/b) Σ_(n=0) ^∞ e^(−nλπ) .∫_0 ^π e^(−λy) siny dy we have ∫_0 ^π e^(−λy) siny dy =Im(∫_0 ^π e^(−λy+iy) dy) and ∫_0 ^π e^((−λ+i)y) dy =[(1/(−λ+i))e^((−λ+i)y) ]_0 ^π =((−1)/(λ−i)){e^((−λ+i)π) −1} =((−(λ+i))/(1+λ^2 )){− e^(−λπ) −1} =(((λ+i)(e^(−λπ) +1))/(1+λ^2 )) ⇒∫_0 ^π e^(−λy) siny dy =((1+e^(−λπ) )/(1+λ^2 )) ⇒ Φ =((1+e^(−λπ) )/(b(1+λ^2 )))Σ_(n=0) ^∞ (e^(−λπ) )^n =((1+e^(−λπ) )/(b(1+λ^2 )))×(1/(1−e^(−λπ) )) ⇒ Φ =((1+e^(−((aπ)/b)) )/(b(1−e^(−((aπ)/b)) )(1+(a^2 /b^2 )))) ⇒Φ=(b/(a^2 +b^2 ))×((1+e^(−((aπ)/b)) )/(1−e^(−((aπ)/b)) ))](Q137122.png) | ||
| ||