
Question and Answers Forum
Question Number 136968 by Eric002 last updated on 28/Mar/21
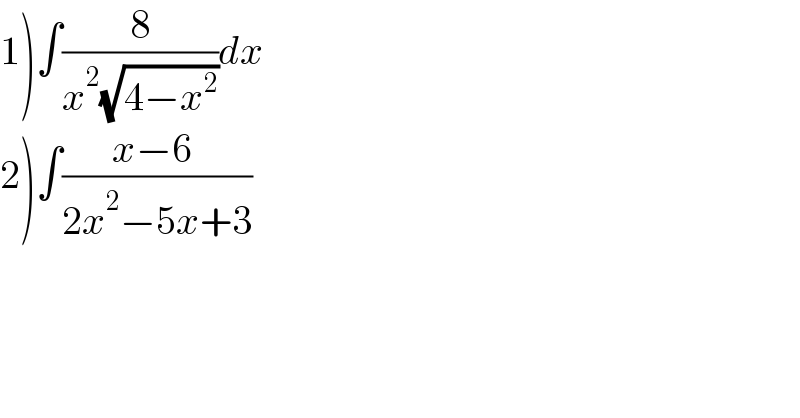
Answered by EDWIN88 last updated on 28/Mar/21
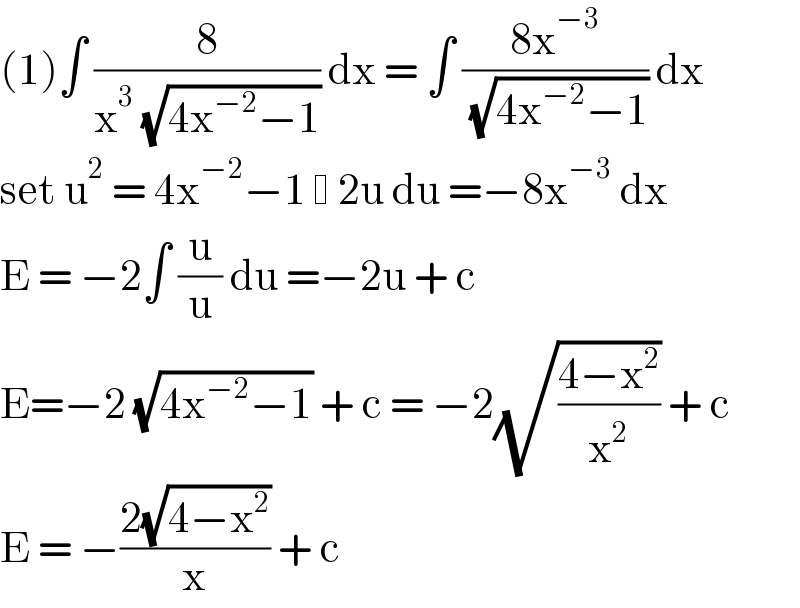
Answered by EDWIN88 last updated on 28/Mar/21
![(2)E=∫ ((x−6)/((2x+1)(x−3))) dx Partial fraction ((x−6)/(2x^2 −5x+3)) = (p/(2x+1)) + (q/(x−3)) where { ((p=[((x−6)/(x−3)) ] _(x=−(1/2)) = ((−13)/(−7))=((13)/7))),((q=[((x−6)/(2x+1)) ]_(x=3) =−(3/7))) :} E=((13)/7)∫ (dx/(2x+1)) −(3/7)∫ (dx/(x−3)) E=((13)/(14)) ln ∣2x+1∣−(3/7) ln ∣x−3∣ + c](Q136975.png)
Answered by mathmax by abdo last updated on 28/Mar/21
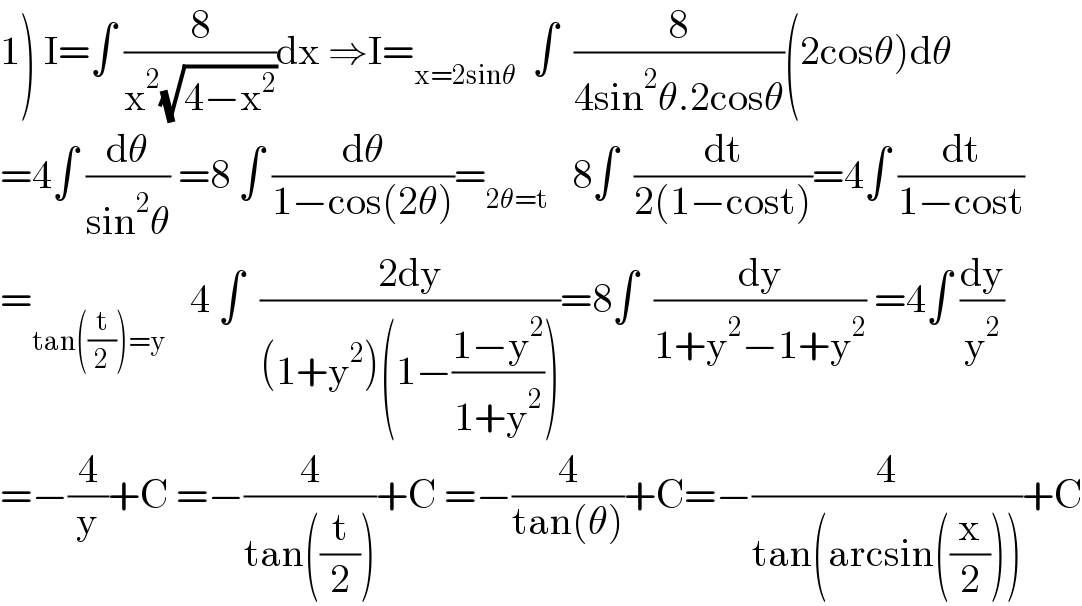
| ||
Question and Answers Forum | ||
Question Number 136968 by Eric002 last updated on 28/Mar/21 | ||
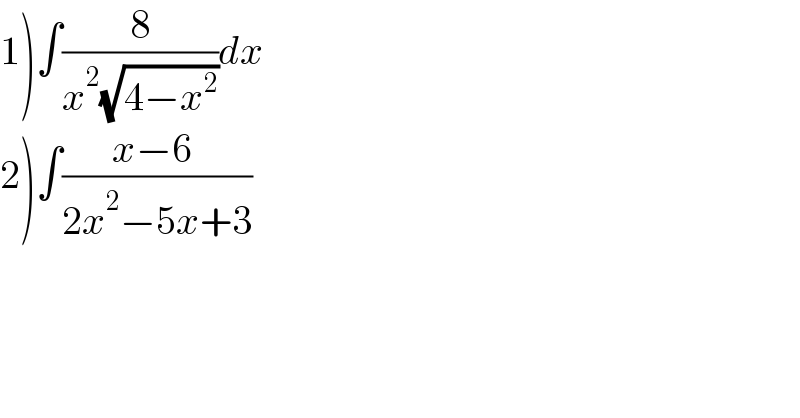 | ||
Answered by EDWIN88 last updated on 28/Mar/21 | ||
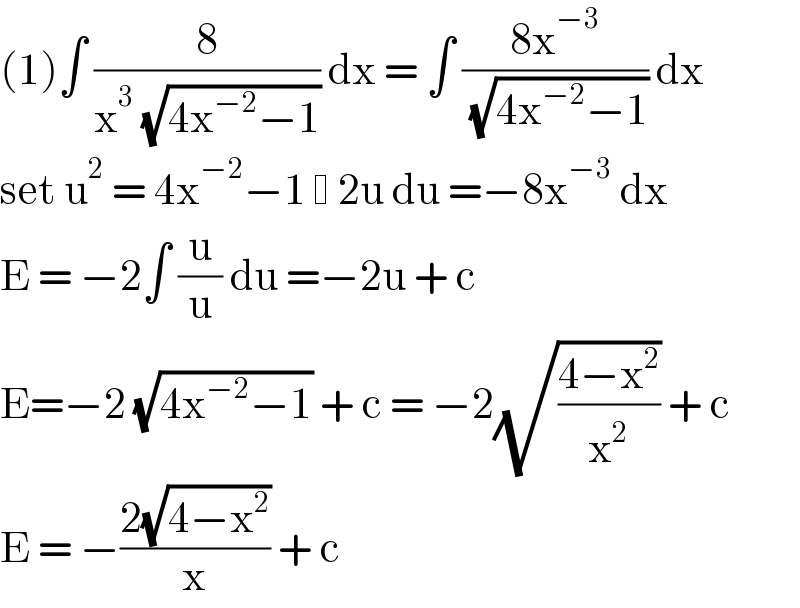 | ||
| ||
Answered by EDWIN88 last updated on 28/Mar/21 | ||
![(2)E=∫ ((x−6)/((2x+1)(x−3))) dx Partial fraction ((x−6)/(2x^2 −5x+3)) = (p/(2x+1)) + (q/(x−3)) where { ((p=[((x−6)/(x−3)) ] _(x=−(1/2)) = ((−13)/(−7))=((13)/7))),((q=[((x−6)/(2x+1)) ]_(x=3) =−(3/7))) :} E=((13)/7)∫ (dx/(2x+1)) −(3/7)∫ (dx/(x−3)) E=((13)/(14)) ln ∣2x+1∣−(3/7) ln ∣x−3∣ + c](Q136975.png) | ||
| ||
Answered by mathmax by abdo last updated on 28/Mar/21 | ||
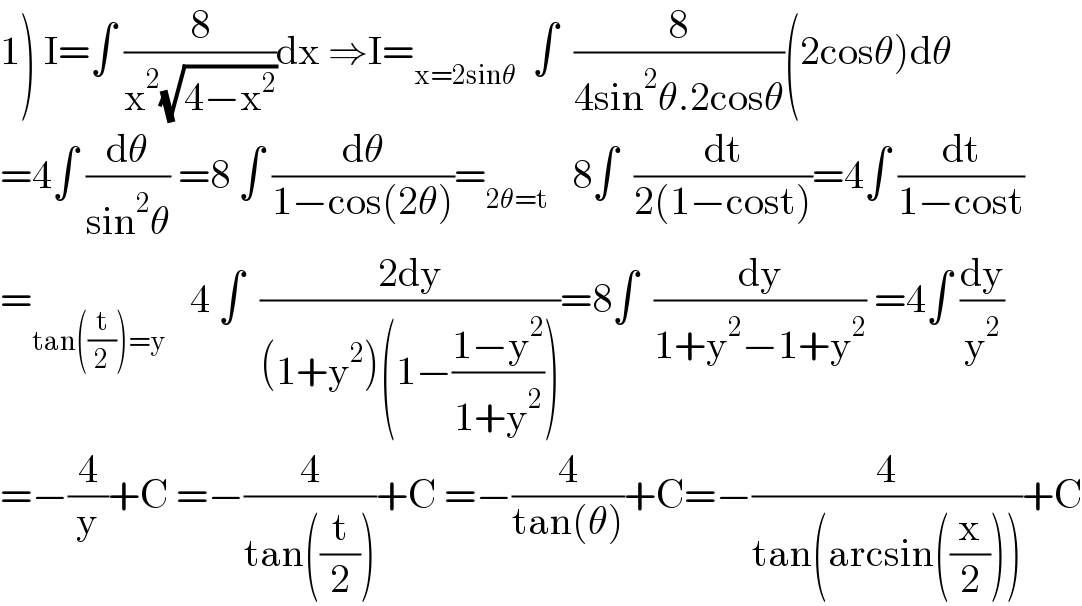 | ||
| ||