Question and Answers Forum

All Questions      Topic List

None Questions

Previous in All Question      Next in All Question      

Previous in None      Next in None      

Question Number 137011 by mohammad17 last updated on 28/Mar/21

Commented by mohammad17 last updated on 28/Mar/21

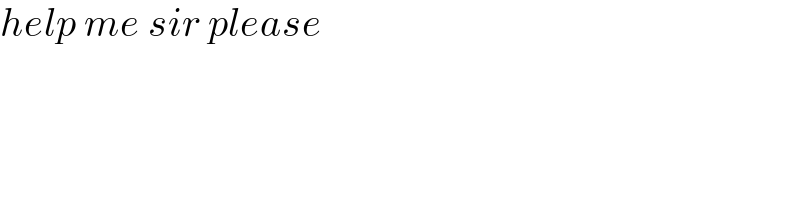
help me sir please

$${help}\:{me}\:{sir}\:{please} \\ $$

Commented by mohammad17 last updated on 28/Mar/21

?????

$$????? \\ $$

Answered by Dwaipayan Shikari last updated on 28/Mar/21

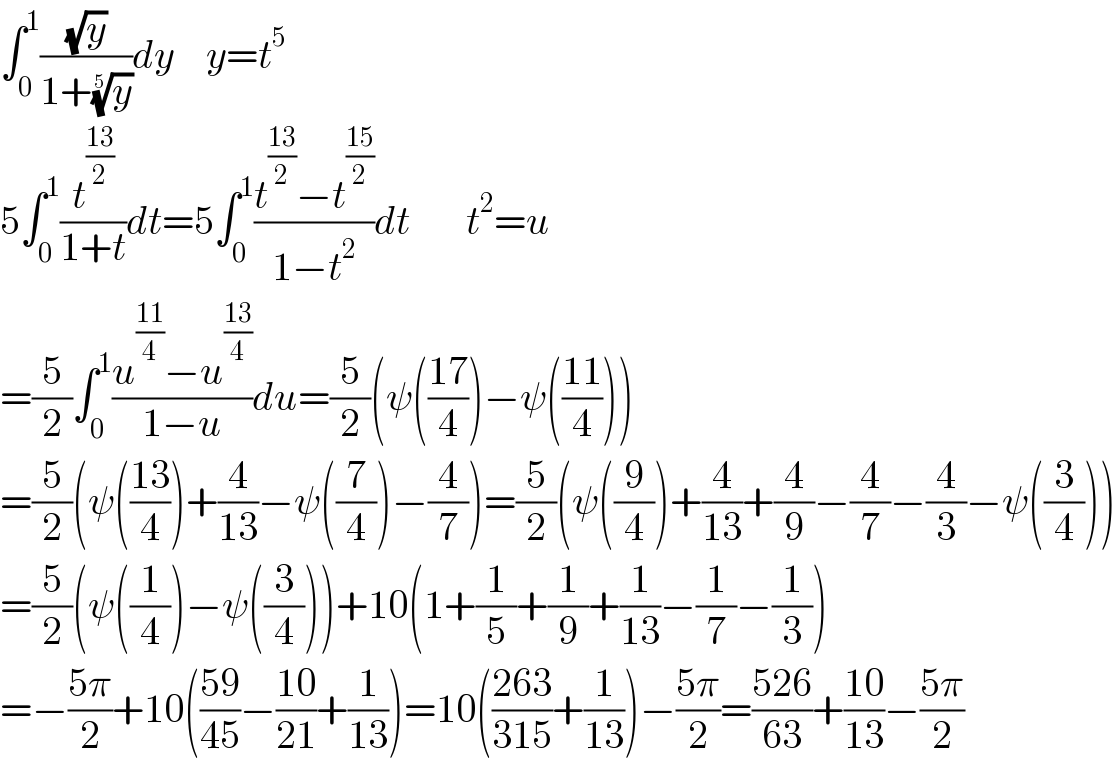
∫_0 ^1 ((√y)/(1+(y)^(1/5) ))dy y=t^5 5∫_0 ^1 (t^((13)/2) /(1+t))dt=5∫_0 ^1 ((t^((13)/2) −t^((15)/2) )/(1−t^2 ))dt t^2 =u =(5/2)∫_0 ^1 ((u^((11)/4) −u^((13)/4) )/(1−u))du=(5/2)(ψ(((17)/4))−ψ(((11)/4))) =(5/2)(ψ(((13)/4))+(4/(13))−ψ((7/4))−(4/7))=(5/2)(ψ((9/4))+(4/(13))+(4/9)−(4/7)−(4/3)−ψ((3/4))) =(5/2)(ψ((1/4))−ψ((3/4)))+10(1+(1/5)+(1/9)+(1/(13))−(1/7)−(1/3)) =−((5π)/2)+10(((59)/(45))−((10)/(21))+(1/(13)))=10(((263)/(315))+(1/(13)))−((5π)/2)=((526)/(63))+((10)/(13))−((5π)/2)

$$\int_{\mathrm{0}} ^{\mathrm{1}} \frac{\sqrt{{y}}}{\mathrm{1}+\sqrt[{\mathrm{5}}]{{y}}}{dy}\:\:\:\:{y}={t}^{\mathrm{5}} \\ $$$$\mathrm{5}\int_{\mathrm{0}} ^{\mathrm{1}} \frac{{t}^{\frac{\mathrm{13}}{\mathrm{2}}} }{\mathrm{1}+{t}}{dt}=\mathrm{5}\int_{\mathrm{0}} ^{\mathrm{1}} \frac{{t}^{\frac{\mathrm{13}}{\mathrm{2}}} −{t}^{\frac{\mathrm{15}}{\mathrm{2}}} }{\mathrm{1}−{t}^{\mathrm{2}} }{dt}\:\:\:\:\:\:\:{t}^{\mathrm{2}} ={u} \\ $$$$=\frac{\mathrm{5}}{\mathrm{2}}\int_{\mathrm{0}} ^{\mathrm{1}} \frac{{u}^{\frac{\mathrm{11}}{\mathrm{4}}} −{u}^{\frac{\mathrm{13}}{\mathrm{4}}} }{\mathrm{1}−{u}}{du}=\frac{\mathrm{5}}{\mathrm{2}}\left(\psi\left(\frac{\mathrm{17}}{\mathrm{4}}\right)−\psi\left(\frac{\mathrm{11}}{\mathrm{4}}\right)\right) \\ $$$$=\frac{\mathrm{5}}{\mathrm{2}}\left(\psi\left(\frac{\mathrm{13}}{\mathrm{4}}\right)+\frac{\mathrm{4}}{\mathrm{13}}−\psi\left(\frac{\mathrm{7}}{\mathrm{4}}\right)−\frac{\mathrm{4}}{\mathrm{7}}\right)=\frac{\mathrm{5}}{\mathrm{2}}\left(\psi\left(\frac{\mathrm{9}}{\mathrm{4}}\right)+\frac{\mathrm{4}}{\mathrm{13}}+\frac{\mathrm{4}}{\mathrm{9}}−\frac{\mathrm{4}}{\mathrm{7}}−\frac{\mathrm{4}}{\mathrm{3}}−\psi\left(\frac{\mathrm{3}}{\mathrm{4}}\right)\right) \\ $$$$=\frac{\mathrm{5}}{\mathrm{2}}\left(\psi\left(\frac{\mathrm{1}}{\mathrm{4}}\right)−\psi\left(\frac{\mathrm{3}}{\mathrm{4}}\right)\right)+\mathrm{10}\left(\mathrm{1}+\frac{\mathrm{1}}{\mathrm{5}}+\frac{\mathrm{1}}{\mathrm{9}}+\frac{\mathrm{1}}{\mathrm{13}}−\frac{\mathrm{1}}{\mathrm{7}}−\frac{\mathrm{1}}{\mathrm{3}}\right) \\ $$$$=−\frac{\mathrm{5}\pi}{\mathrm{2}}+\mathrm{10}\left(\frac{\mathrm{59}}{\mathrm{45}}−\frac{\mathrm{10}}{\mathrm{21}}+\frac{\mathrm{1}}{\mathrm{13}}\right)=\mathrm{10}\left(\frac{\mathrm{263}}{\mathrm{315}}+\frac{\mathrm{1}}{\mathrm{13}}\right)−\frac{\mathrm{5}\pi}{\mathrm{2}}=\frac{\mathrm{526}}{\mathrm{63}}+\frac{\mathrm{10}}{\mathrm{13}}−\frac{\mathrm{5}\pi}{\mathrm{2}} \\ $$

Commented by mohammad17 last updated on 28/Mar/21

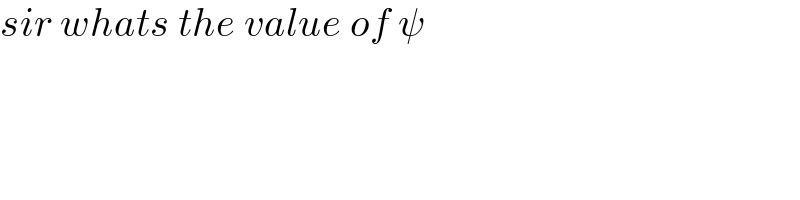
sir whats the value of ψ

$${sir}\:{whats}\:{the}\:{value}\:{of}\:\psi \\ $$

Commented by Dwaipayan Shikari last updated on 28/Mar/21

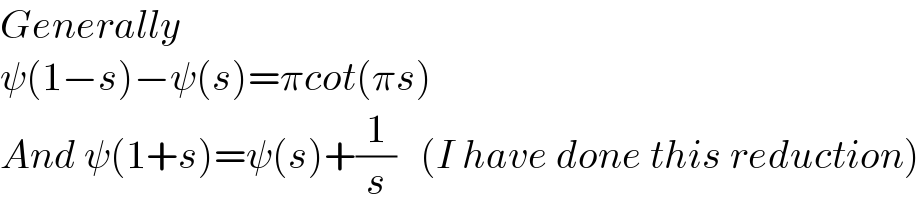
Generally ψ(1−s)−ψ(s)=πcot(πs) And ψ(1+s)=ψ(s)+(1/s) (I have done this reduction)

$${Generally}\: \\ $$$$\psi\left(\mathrm{1}−{s}\right)−\psi\left({s}\right)=\pi{cot}\left(\pi{s}\right) \\ $$$${And}\:\psi\left(\mathrm{1}+{s}\right)=\psi\left({s}\right)+\frac{\mathrm{1}}{{s}}\:\:\:\left({I}\:{have}\:{done}\:{this}\:{reduction}\right) \\ $$

Answered by mathmax by abdo last updated on 29/Mar/21

1)I=∫_0 ^1 ((√x)/(1+x^(1/5) ))dx (at form of serie) ⇒I=_((√x)=t) ∫_0 ^1 (t/(1+t^(2/5) ))(2t)dt =2∫_0 ^1 (t^2 /(1+t^(2/5) ))dt changement t^(2/5) =y give t=y^(5/2) ⇒ I=2.(5/2) ∫_0 ^1 (y^5 /(1+y)) y^((5/2)−1) dy =5∫_0 ^1 (y^(((15)/2)−1) /(1+y))dy =5 ∫_0 ^1 y^((13)/2) Σ_(n=0) ^∞ (−1)^n y^n dy =5 Σ_(n=0) ^∞ (−1)^n ∫_0 ^1 y^(n+((13)/2)) dy =5Σ_(n=0) ^∞ (−1)^n (1/(n+((13)/2)+1))[y^(n+((13)/2)+1) ]_0 ^1 =5Σ_(n=0) ^∞ (((−1)^n )/(n+((15)/2))) =10 Σ_(n=0) ^∞ (((−1)^n )/(2n+15)) rest to find the value of this serie ...be continued...

$$\left.\mathrm{1}\right)\mathrm{I}=\int_{\mathrm{0}} ^{\mathrm{1}} \:\frac{\sqrt{\mathrm{x}}}{\mathrm{1}+\mathrm{x}^{\frac{\mathrm{1}}{\mathrm{5}}} }\mathrm{dx}\:\:\:\left(\mathrm{at}\:\mathrm{form}\:\mathrm{of}\:\mathrm{serie}\right)\:\Rightarrow\mathrm{I}=_{\sqrt{\mathrm{x}}=\mathrm{t}} \:\:\:\int_{\mathrm{0}} ^{\mathrm{1}} \:\frac{\mathrm{t}}{\mathrm{1}+\mathrm{t}^{\frac{\mathrm{2}}{\mathrm{5}}} }\left(\mathrm{2t}\right)\mathrm{dt} \\ $$$$=\mathrm{2}\int_{\mathrm{0}} ^{\mathrm{1}} \:\frac{\mathrm{t}^{\mathrm{2}} }{\mathrm{1}+\mathrm{t}^{\frac{\mathrm{2}}{\mathrm{5}}} }\mathrm{dt}\:\:\:\:\:\:\mathrm{changement}\:\:\mathrm{t}^{\frac{\mathrm{2}}{\mathrm{5}}} \:=\mathrm{y}\:\mathrm{give}\:\mathrm{t}=\mathrm{y}^{\frac{\mathrm{5}}{\mathrm{2}}} \:\Rightarrow \\ $$$$\mathrm{I}=\mathrm{2}.\frac{\mathrm{5}}{\mathrm{2}}\:\int_{\mathrm{0}} ^{\mathrm{1}} \:\frac{\mathrm{y}^{\mathrm{5}} }{\mathrm{1}+\mathrm{y}}\:\mathrm{y}^{\frac{\mathrm{5}}{\mathrm{2}}−\mathrm{1}} \:\mathrm{dy}\:=\mathrm{5}\int_{\mathrm{0}} ^{\mathrm{1}} \:\frac{\mathrm{y}^{\frac{\mathrm{15}}{\mathrm{2}}−\mathrm{1}} }{\mathrm{1}+\mathrm{y}}\mathrm{dy} \\ $$$$=\mathrm{5}\:\int_{\mathrm{0}} ^{\mathrm{1}} \:\mathrm{y}^{\frac{\mathrm{13}}{\mathrm{2}}} \sum_{\mathrm{n}=\mathrm{0}} ^{\infty} \:\left(−\mathrm{1}\right)^{\mathrm{n}} \:\mathrm{y}^{\mathrm{n}} \:\mathrm{dy} \\ $$$$=\mathrm{5}\:\sum_{\mathrm{n}=\mathrm{0}} ^{\infty} \:\left(−\mathrm{1}\right)^{\mathrm{n}} \:\int_{\mathrm{0}} ^{\mathrm{1}} \:\mathrm{y}^{\mathrm{n}+\frac{\mathrm{13}}{\mathrm{2}}} \:\mathrm{dy} \\ $$$$=\mathrm{5}\sum_{\mathrm{n}=\mathrm{0}} ^{\infty} \left(−\mathrm{1}\right)^{\mathrm{n}} \:\frac{\mathrm{1}}{\mathrm{n}+\frac{\mathrm{13}}{\mathrm{2}}+\mathrm{1}}\left[\mathrm{y}^{\mathrm{n}+\frac{\mathrm{13}}{\mathrm{2}}+\mathrm{1}} \right]_{\mathrm{0}} ^{\mathrm{1}} \\ $$$$=\mathrm{5}\sum_{\mathrm{n}=\mathrm{0}} ^{\infty} \:\:\:\frac{\left(−\mathrm{1}\right)^{\mathrm{n}} }{\mathrm{n}+\frac{\mathrm{15}}{\mathrm{2}}}\:=\mathrm{10}\:\sum_{\mathrm{n}=\mathrm{0}} ^{\infty} \:\frac{\left(−\mathrm{1}\right)^{\mathrm{n}} }{\mathrm{2n}+\mathrm{15}} \\ $$$$\mathrm{rest}\:\mathrm{to}\:\mathrm{find}\:\mathrm{the}\:\mathrm{value}\:\mathrm{of}\:\mathrm{this}\:\mathrm{serie}\:...\mathrm{be}\:\mathrm{continued}... \\ $$

Answered by mathmax by abdo last updated on 29/Mar/21

Φ=∫_0 ^∞ e^((−(y^2 −3y))/(a^2 +b^2 )) dy ⇒Φ=∫_0 ^∞ e^(−{y^2 −2(3/2)y +(9/4)−(9/4)}×(1/(a^2 +b^2 ))) dy =∫_0 ^∞ e^((−(y−(3/2))^2 +(9/4))/(a^2 +b^2 )) dy =e^(9/(4(a^2 +b^2 ))) ∫_0 ^∞ e^(−(((y−(3/2))/( (√(a^2 +b^2 )))))^2 ) dy =_(((y−(3/2))/( (√(a^2 +b^2 ))))=z) e^(9/(4(a^2 +b^2 ))) .∫_(−(3/(2(√(a^2 +b^2 ))))) ^∞ e^(−z^2 ) (√(a^2 +b^2 ))dz =(√(a^2 +b^2 )).e^(9/(4(a^2 +b^2 ))) { ∫_(−(3/(2(√(a^2 +b^2 ))))) ^0 e^(−z^2 ) dz +((√π)/2)} we have ∫_(−(3/(2(√(a^2 +b^2 ))))) ^0 e^(−z^2 ) dz =_(z=−u) −∫_0 ^(3/(2(√(a^2 +b^2 )))) e^(−u^2 ) (−du) ⇒ Φ =(√(a^2 +b^2 )).e^(9/(4(a^2 +b^2 ))) { ((√π)/2) +∫_0 ^(3/(2(√(a^2 +b^2 )))) e^(−z^2 ) dz}

$$\Phi=\int_{\mathrm{0}} ^{\infty} \:\:\mathrm{e}^{\frac{−\left(\mathrm{y}^{\mathrm{2}} −\mathrm{3y}\right)}{\mathrm{a}^{\mathrm{2}} \:+\mathrm{b}^{\mathrm{2}} }} \:\mathrm{dy}\:\Rightarrow\Phi=\int_{\mathrm{0}} ^{\infty} \:\:\mathrm{e}^{−\left\{\mathrm{y}^{\mathrm{2}} −\mathrm{2}\frac{\mathrm{3}}{\mathrm{2}}\mathrm{y}\:+\frac{\mathrm{9}}{\mathrm{4}}−\frac{\mathrm{9}}{\mathrm{4}}\right\}×\frac{\mathrm{1}}{\mathrm{a}^{\mathrm{2}} \:+\mathrm{b}^{\mathrm{2}} }} \:\mathrm{dy} \\ $$$$=\int_{\mathrm{0}} ^{\infty} \:\:\mathrm{e}^{\frac{−\left(\mathrm{y}−\frac{\mathrm{3}}{\mathrm{2}}\right)^{\mathrm{2}} +\frac{\mathrm{9}}{\mathrm{4}}}{\mathrm{a}^{\mathrm{2}} \:+\mathrm{b}^{\mathrm{2}} }} \:\mathrm{dy}\:=\mathrm{e}^{\frac{\mathrm{9}}{\mathrm{4}\left(\mathrm{a}^{\mathrm{2}} +\mathrm{b}^{\mathrm{2}} \right)}} \:\int_{\mathrm{0}} ^{\infty} \:\:\mathrm{e}^{−\left(\frac{\mathrm{y}−\frac{\mathrm{3}}{\mathrm{2}}}{\:\sqrt{\mathrm{a}^{\mathrm{2}} +\mathrm{b}^{\mathrm{2}} }}\right)^{\mathrm{2}} } \:\mathrm{dy} \\ $$$$=_{\frac{\mathrm{y}−\frac{\mathrm{3}}{\mathrm{2}}}{\:\sqrt{\mathrm{a}^{\mathrm{2}} +\mathrm{b}^{\mathrm{2}} }}=\mathrm{z}} \:\:\:\mathrm{e}^{\frac{\mathrm{9}}{\mathrm{4}\left(\mathrm{a}^{\mathrm{2}} \:+\mathrm{b}^{\mathrm{2}} \right)}} \:.\int_{−\frac{\mathrm{3}}{\mathrm{2}\sqrt{\mathrm{a}^{\mathrm{2}} +\mathrm{b}^{\mathrm{2}} }}} ^{\infty} \:\mathrm{e}^{−\mathrm{z}^{\mathrm{2}} } \sqrt{\mathrm{a}^{\mathrm{2}} +\mathrm{b}^{\mathrm{2}} }\mathrm{dz} \\ $$$$=\sqrt{\mathrm{a}^{\mathrm{2}} +\mathrm{b}^{\mathrm{2}} }.\mathrm{e}^{\frac{\mathrm{9}}{\mathrm{4}\left(\mathrm{a}^{\mathrm{2}} +\mathrm{b}^{\mathrm{2}} \right)}} \:\left\{\:\int_{−\frac{\mathrm{3}}{\mathrm{2}\sqrt{\mathrm{a}^{\mathrm{2}} +\mathrm{b}^{\mathrm{2}} }}} ^{\mathrm{0}} \:\mathrm{e}^{−\mathrm{z}^{\mathrm{2}} } \mathrm{dz}\:+\frac{\sqrt{\pi}}{\mathrm{2}}\right\} \\ $$$$\mathrm{we}\:\mathrm{have}\:\int_{−\frac{\mathrm{3}}{\mathrm{2}\sqrt{\mathrm{a}^{\mathrm{2}} +\mathrm{b}^{\mathrm{2}} }}} ^{\mathrm{0}} \:\mathrm{e}^{−\mathrm{z}^{\mathrm{2}} } \mathrm{dz}\:=_{\mathrm{z}=−\mathrm{u}} \:\:\:−\int_{\mathrm{0}} ^{\frac{\mathrm{3}}{\mathrm{2}\sqrt{\mathrm{a}^{\mathrm{2}} +\mathrm{b}^{\mathrm{2}} }}} \:\:\:\mathrm{e}^{−\mathrm{u}^{\mathrm{2}} } \left(−\mathrm{du}\right)\:\Rightarrow \\ $$$$\Phi\:=\sqrt{\mathrm{a}^{\mathrm{2}} +\mathrm{b}^{\mathrm{2}} }.\mathrm{e}^{\frac{\mathrm{9}}{\mathrm{4}\left(\mathrm{a}^{\mathrm{2}} \:+\mathrm{b}^{\mathrm{2}} \right)}} \:\left\{\:\frac{\sqrt{\pi}}{\mathrm{2}}\:+\int_{\mathrm{0}} ^{\frac{\mathrm{3}}{\mathrm{2}\sqrt{\mathrm{a}^{\mathrm{2}} \:+\mathrm{b}^{\mathrm{2}} }}} \:\:\:\:\mathrm{e}^{−\mathrm{z}^{\mathrm{2}} } \mathrm{dz}\right\} \\ $$

Answered by mathmax by abdo last updated on 29/Mar/21

3) I=∫_(−1) ^1 (e^(2y) /( (√7)+e^y ))dy we do the chanhement e^y =x ⇒ I =∫_(1/e) ^e (x^2 /( (√7)+x))(dx/x) =∫_(1/e) ^e (x/(x+(√7)))dx =∫_(1/e) ^e ((x+(√7)−(√7))/(x+(√7)))dx =[x]_(1/e) ^e −(√7)[ln(x+(√7))]_(1/e) ^e =e−e^(−1) −(√7){ln(e+(√7))−ln(e^(−1) +(√7))}

$$\left.\mathrm{3}\right)\:\mathrm{I}=\int_{−\mathrm{1}} ^{\mathrm{1}} \:\frac{\mathrm{e}^{\mathrm{2y}} }{\:\sqrt{\mathrm{7}}+\mathrm{e}^{\mathrm{y}} }\mathrm{dy}\:\:\mathrm{we}\:\mathrm{do}\:\mathrm{the}\:\mathrm{chanhement}\:\mathrm{e}^{\mathrm{y}} =\mathrm{x}\:\Rightarrow \\ $$$$\mathrm{I}\:=\int_{\frac{\mathrm{1}}{\mathrm{e}}} ^{\mathrm{e}} \:\:\frac{\mathrm{x}^{\mathrm{2}} }{\:\sqrt{\mathrm{7}}+\mathrm{x}}\frac{\mathrm{dx}}{\mathrm{x}}\:=\int_{\frac{\mathrm{1}}{\mathrm{e}}} ^{\mathrm{e}} \:\frac{\mathrm{x}}{\mathrm{x}+\sqrt{\mathrm{7}}}\mathrm{dx}\:=\int_{\frac{\mathrm{1}}{\mathrm{e}}} ^{\mathrm{e}} \:\frac{\mathrm{x}+\sqrt{\mathrm{7}}−\sqrt{\mathrm{7}}}{\mathrm{x}+\sqrt{\mathrm{7}}}\mathrm{dx} \\ $$$$=\left[\mathrm{x}\right]_{\frac{\mathrm{1}}{\mathrm{e}}} ^{\mathrm{e}} −\sqrt{\mathrm{7}}\left[\mathrm{ln}\left(\mathrm{x}+\sqrt{\mathrm{7}}\right)\right]_{\frac{\mathrm{1}}{\mathrm{e}}} ^{\mathrm{e}} \:=\mathrm{e}−\mathrm{e}^{−\mathrm{1}} \:−\sqrt{\mathrm{7}}\left\{\mathrm{ln}\left(\mathrm{e}+\sqrt{\mathrm{7}}\right)−\mathrm{ln}\left(\mathrm{e}^{−\mathrm{1}} \:+\sqrt{\mathrm{7}}\right)\right\} \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com