Question and Answers Forum

All Questions      Topic List

Algebra Questions

Previous in All Question      Next in All Question      

Previous in Algebra      Next in Algebra      

Question Number 137037 by JulioCesar last updated on 29/Mar/21

Answered by mathmax by abdo last updated on 29/Mar/21

$$\mathrm{I}=\int \frac{\mathrm{dx}}{{({\mathrm{x}}^3-8)}^2}\left(\mathrm{compolex}\mathrm{method}\right)\Rightarrow \mathrm{I}=\int \frac{\mathrm{dx}}{{(\mathrm{x}-2)}^2{({\mathrm{x}}^2+2\mathrm{x}+4)}^2}$$$${\mathrm{x}}^2+2\mathrm{x}+4=0\to {\mathrm{\Delta }}^{{}^{\prime }}=-3\Rightarrow {\mathrm{x}}_1=-1+\mathrm{i}\sqrt{3}=2(-\frac{1}{2}+\frac{\mathrm{i}\sqrt{3}}{2})={2\mathrm{e}}^{\frac{2\mathrm{i}\pi }{3}}$$$${\mathrm{x}}_2=-1-\mathrm{i}\sqrt{3}={2\mathrm{e}}^{-\frac{2\mathrm{i}\pi }{3}}\Rightarrow \mathrm{I}=\int \frac{\mathrm{dx}}{{(\mathrm{x}-2)}^2{(\mathrm{x}-{2\mathrm{e}}^{\frac{2\mathrm{i}\pi }{3}})}^2(\mathrm{x}-{\mathrm{e}}^{-\frac{2\mathrm{i}\pi }{3}})}$$$$=\int \frac{\mathrm{dx}}{{(\mathrm{x}-2)}^2{\left(\frac{\mathrm{x}-{\mathrm{e}}^{\frac{2\mathrm{i}\pi }{3}}}{\mathrm{x}-{\mathrm{e}}^{-\frac{2\mathrm{i}\pi }{3}}}\right)}^2{(\mathrm{x}-{\mathrm{e}}^{-\frac{2\mathrm{i}\pi }{3}})}^4}$$$$\mathrm{changement}\frac{\mathrm{x}-{\mathrm{e}}^{\frac{2\mathrm{i}\pi }{3}}}{\mathrm{x}-{\mathrm{e}}^{-\frac{2\mathrm{i}\pi }{3}}}=\mathrm{z}\Rightarrow \mathrm{x}-{\mathrm{e}}^{\frac{2\mathrm{i}\pi }{3}}=\mathrm{zx}-{\mathrm{e}}^{-\frac{2\mathrm{i}\pi }{3}}\mathrm{z}\Rightarrow$$$$(1-\mathrm{z})\mathrm{x}={\mathrm{e}}^{\frac{2\mathrm{i}\pi }{3}}-{\mathrm{e}}^{-\frac{2\mathrm{i}\pi }{3}}\mathrm{z}\Rightarrow \mathrm{x}=\frac{{\mathrm{e}}^{-\frac{2\mathrm{i}\pi }{3}}\mathrm{z}-{\mathrm{e}}^{\frac{2\mathrm{i}\pi }{3}}}{\mathrm{z}-1}\Rightarrow$$$$\frac{\mathrm{dx}}{\mathrm{dz}}=\frac{{\mathrm{e}}^{-\frac{2\mathrm{i}\pi }{3}}(\mathrm{z}-1)-{\mathrm{e}}^{-\frac{2\mathrm{i}\pi }{3}}\mathrm{z}+{\mathrm{e}}^{\frac{2\mathrm{i}\pi }{3}}}{{(\mathrm{z}-1)}^2}=\frac{2\mathrm{isin}\left(\frac{\pi }{3}\right)}{{(\mathrm{z}-1)}^2}=\frac{2\mathrm{i}\frac{\sqrt{3}}{2}}{{(\mathrm{z}-1)}^2}=\frac{\mathrm{i}\sqrt{3}}{{(\mathrm{z}-1)}^2}$$$$\mathrm{x}-2=\frac{{\mathrm{e}}^{-\frac{2\mathrm{i}\pi }{3}}\mathrm{z}-{\mathrm{e}}^{\frac{2\mathrm{i}\pi }{3}}}{\mathrm{z}-1}-2=\frac{{\mathrm{e}}^{-\frac{2\mathrm{i}\pi }{3}}\mathrm{z}-{\mathrm{e}}^{\frac{2\mathrm{i}\pi }{3}}-2\mathrm{z}+2}{\mathrm{z}-1}$$$$\mathrm{x}-{\mathrm{e}}^{-\frac{2\mathrm{i}\pi }{3}}=\frac{{\mathrm{e}}^{-\frac{2\mathrm{i}\pi }{3}}\mathrm{z}-{\mathrm{e}}^{\frac{2\mathrm{i}\pi }{3}}}{\mathrm{z}-1}-{\mathrm{e}}^{\frac{-2\mathrm{i}\pi }{3}}=\frac{-{\mathrm{e}}^{\frac{2\mathrm{i}\pi }{3}}+{\mathrm{e}}^{-\frac{2\mathrm{i}\pi }{3}}}{\mathrm{z}-1}=\frac{-\mathrm{i}\sqrt{3}}{(\mathrm{z}-1)}\Rightarrow$$$$\mathrm{I}=\int \frac{1}{{\left(\frac{({\mathrm{e}}^{-\frac{2\mathrm{i}\pi }{3}}-2)\mathrm{z}+2-{\mathrm{e}}^{\frac{2\mathrm{i}\pi }{3}}}{\mathrm{z}-1}\right)}^2.{\mathrm{z}}^2{\left(\frac{-\mathrm{i}\sqrt{3}}{\mathrm{z}-1}\right)}^4}\frac{\mathrm{i}\sqrt{3}}{{(\mathrm{z}-1)}^2}\mathrm{dz}$$$$=\frac{1}{{\left(\mathrm{i}\sqrt{3}\right)}^3}\int \frac{{(\mathrm{z}-1)}^4}{{\mathrm{z}}^2{(\alpha \mathrm{z}+\beta )}^2}\mathrm{dz}(\alpha =({\mathrm{e}}^{-\frac{2\mathrm{i}\pi }{3}}-2)\mathrm{and}\beta =2-{\mathrm{e}}^{\frac{2\mathrm{i}\pi }{3}})\mathrm{but}$$$$\int \frac{{(\mathrm{z}-1)}^4}{{\mathrm{z}}^2{(\alpha \mathrm{z}+\beta )}^2}\mathrm{dz}=\int \frac{1}{{\mathrm{z}}^2{(\alpha \mathrm{z}+\beta )}^2}\sum _{\mathrm{k}=0}^4{\mathrm{C}}_4^{\mathrm{k}}{\mathrm{z}}^{\mathrm{k}}{(-1)}^{4-\mathrm{k}}\mathrm{dz}$$$$=\sum _{\mathrm{k}0}^4{\mathrm{C}}_4^{\mathrm{k}}{(-1)}^{\mathrm{k}}\int \frac{{\mathrm{z}}^{\mathrm{k}-2}}{{(\alpha \mathrm{z}+\beta )}^2}\mathrm{dz}$$$${=}_{\alpha \mathrm{z}+\beta =\mathrm{t}}\sum _{\mathrm{k}=0}^4{\mathrm{C}}_4^{\mathrm{k}}{(-1)}^{\mathrm{k}}\int \frac{{\left(\frac{\mathrm{t}-\beta }{\alpha }\right)}^{\mathrm{k}-2}}{{\mathrm{t}}^2}\frac{\mathrm{dt}}{\alpha }$$$$=\sum _{\mathrm{k}=0}^4{(-1)}^{\mathrm{k}}{\mathrm{C}}_4^{\mathrm{k}}\frac{1}{{\alpha }^{\mathrm{k}-1}}\int \frac{{(\mathrm{t}-\beta )}^{\mathrm{k}-2}}{{\mathrm{t}}^2}\mathrm{dt}\mathrm{and}$$$${\mathrm{I}}_{\mathrm{k}}=\int \frac{{(\mathrm{t}-\beta )}^{\mathrm{k}-2}}{{\mathrm{t}}^2}\mathrm{dt}\mathrm{are}\mathrm{eazy}\mathrm{to}\mathrm{find}....$$

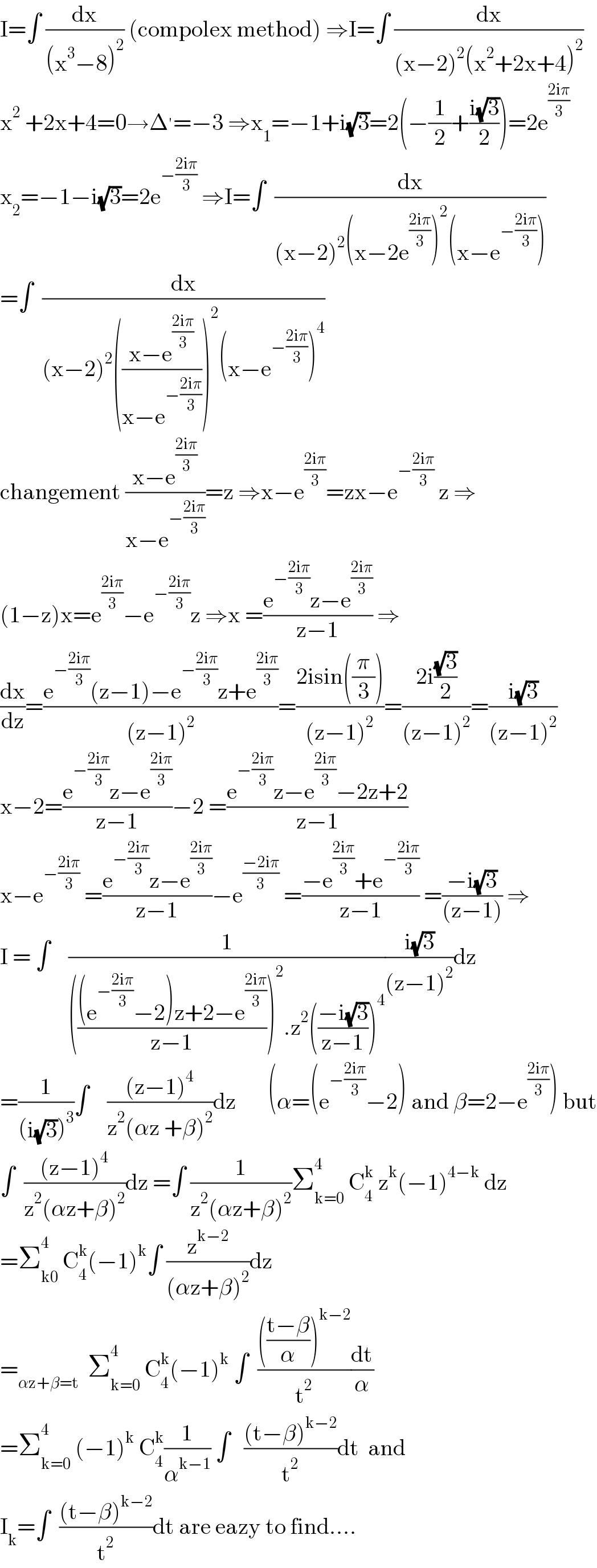
Answered by MJS_new last updated on 30/Mar/21

$$\int \frac{dx}{{(x^3-8)}^2}=$$$$\left[\mathrm{Ostrogradski}\right]$$$$=-\frac{x}{24(x^3-8)}-\frac{1}{12}\int \frac{dx}{x^3-8}=$$$$=-\frac{x}{24(x^3-8)}-\frac{1}{144}\int \frac{dx}{x-2}+\frac{1}{144}\int \frac{x+4}{x^2+2x+4}dx=$$$$=-\frac{x}{24(x^3-8)}-\frac{\ln \mid x-2\mid }{144}+\frac{1}{288}\int \frac{2x+2}{x^2+2x+4}dx+\frac{1}{48}\int \frac{dx}{x^2+2x+4}=$$$$=-\frac{x}{24(x^3-8)}-\frac{\ln \mid x-2\mid }{144}+\frac{\ln (x^2+2x+4)}{288}+\frac{\sqrt{3}\arctan \frac{x+1}{\sqrt{3}}}{144}+C$$

Commented by JulioCesar last updated on 02/Apr/21

I don't understand sir

Terms of Service

Privacy Policy

Contact: info@tinkutara.com