Question and Answers Forum

All Questions      Topic List

Number Theory Questions

Previous in All Question      Next in All Question      

Previous in Number Theory      Next in Number Theory      

Question Number 13744 by AH Soomro last updated on 23/May/17

Solve the following 7^x ≡13(mod 18) Pl give complete process.

$${Solve}\:{the}\:{following} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\mathrm{7}^{{x}} \equiv\mathrm{13}\left({mod}\:\mathrm{18}\right) \\ $$$${Pl}\:{give}\:{complete}\:{process}. \\ $$

Commented by prakash jain last updated on 23/May/17

7≡7 (mod 18) 7^2 =49≡13 (mod 18) 7^3 =343≡1 (mod 18) 7^(3n) ≡1 (mod 18) 7^(3n+1) ≡7(mod 18) 7^(3n+2) ≡13 (mod 18) x=3n+2, n∈{0,1,2...}

$$\mathrm{7}\equiv\mathrm{7}\:\left(\mathrm{mod}\:\mathrm{18}\right) \\ $$$$\mathrm{7}^{\mathrm{2}} =\mathrm{49}\equiv\mathrm{13}\:\left(\mathrm{mod}\:\mathrm{18}\right) \\ $$$$\mathrm{7}^{\mathrm{3}} =\mathrm{343}\equiv\mathrm{1}\:\left(\mathrm{mod}\:\mathrm{18}\right) \\ $$$$\mathrm{7}^{\mathrm{3n}} \equiv\mathrm{1}\:\left(\mathrm{mod}\:\mathrm{18}\right) \\ $$$$\mathrm{7}^{\mathrm{3}{n}+\mathrm{1}} \equiv\mathrm{7}\left(\mathrm{mod}\:\mathrm{18}\right) \\ $$$$\mathrm{7}^{\mathrm{3}{n}+\mathrm{2}} \equiv\mathrm{13}\:\left(\mathrm{mod}\:\mathrm{18}\right) \\ $$$${x}=\mathrm{3}{n}+\mathrm{2},\:{n}\in\left\{\mathrm{0},\mathrm{1},\mathrm{2}...\right\} \\ $$

Commented by mrW1 last updated on 23/May/17

∮antastiC!

$$\oint{antastiC}! \\ $$

Commented by RasheedSindhi last updated on 24/May/17

We can come directly to third step, because Euler′s theorem tells us that If (a,m)=1, then a^(∅(m)) ≡1(mod m) [ where ∅ is Euler function and ∅(m) is meant number of coprimes of m which are not greater than m.] Hence 7^3 ≡1(mod 18) ∵ ∅(7)=3 and (7,18)=1

$$\mathrm{We}\:\mathrm{can}\:\mathrm{come}\:\mathrm{directly}\:\mathrm{to} \\ $$$$\mathrm{third}\:\mathrm{step},\:\mathrm{because}\:\mathrm{Euler}'\mathrm{s} \\ $$$$\mathrm{theorem}\:\mathrm{tells}\:\mathrm{us}\:\mathrm{that}\: \\ $$$$\:\:\:\:\:\mathrm{If}\:\:\left(\mathrm{a},\mathrm{m}\right)=\mathrm{1},\:\mathrm{then}\: \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\mathrm{a}^{\emptyset\left(\mathrm{m}\right)} \equiv\mathrm{1}\left(\mathrm{mod}\:\mathrm{m}\right) \\ $$$$\:\:\:\:\:\:\:\left[\:\mathrm{where}\:\emptyset\:\mathrm{is}\:\mathrm{Euler}\:\mathrm{function}\right. \\ $$$$\mathrm{and}\:\:\emptyset\left(\mathrm{m}\right)\:\mathrm{is}\:\mathrm{meant}\:\mathrm{number}\:\mathrm{of} \\ $$$$\mathrm{coprimes}\:\mathrm{of}\:\:\mathrm{m}\:\mathrm{which}\:\mathrm{are}\:\mathrm{not} \\ $$$$\left.\:\mathrm{greater}\:\mathrm{than}\:\mathrm{m}.\right] \\ $$$$\mathrm{Hence}\:\mathrm{7}^{\mathrm{3}} \equiv\mathrm{1}\left(\mathrm{mod}\:\mathrm{18}\right) \\ $$$$\because\:\emptyset\left(\mathrm{7}\right)=\mathrm{3}\:\mathrm{and}\:\left(\mathrm{7},\mathrm{18}\right)=\mathrm{1} \\ $$

Commented by AH Soomro last updated on 24/May/17

Thanks to all.

$$\mathrm{Thanks}\:\mathrm{to}\:\mathrm{all}. \\ $$

Answered by mrW1 last updated on 23/May/17

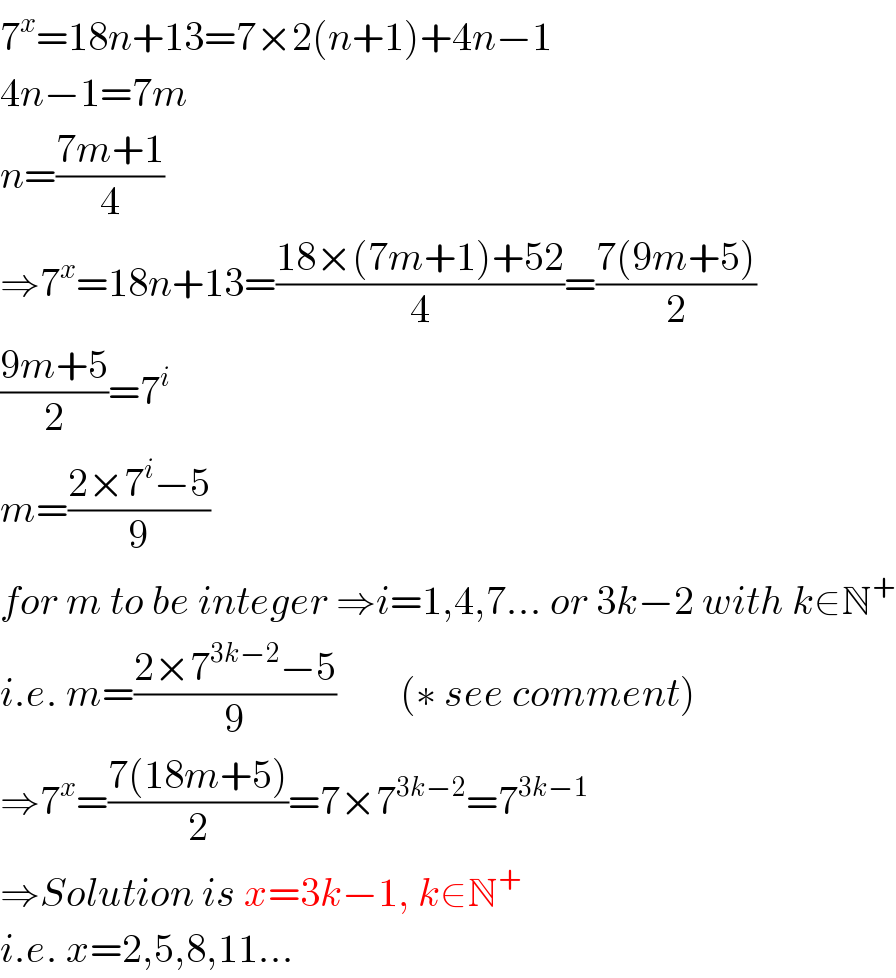
7^x =18n+13=7×2(n+1)+4n−1 4n−1=7m n=((7m+1)/4) ⇒7^x =18n+13=((18×(7m+1)+52)/4)=((7(9m+5))/2) ((9m+5)/2)=7^i m=((2×7^i −5)/9) for m to be integer ⇒i=1,4,7... or 3k−2 with k∈N^+ i.e. m=((2×7^(3k−2) −5)/9) (∗ see comment) ⇒7^x =((7(18m+5))/2)=7×7^(3k−2) =7^(3k−1) ⇒Solution is x=3k−1, k∈N^+ i.e. x=2,5,8,11...

$$\mathrm{7}^{{x}} =\mathrm{18}{n}+\mathrm{13}=\mathrm{7}×\mathrm{2}\left({n}+\mathrm{1}\right)+\mathrm{4}{n}−\mathrm{1} \\ $$$$\mathrm{4}{n}−\mathrm{1}=\mathrm{7}{m} \\ $$$${n}=\frac{\mathrm{7}{m}+\mathrm{1}}{\mathrm{4}} \\ $$$$\Rightarrow\mathrm{7}^{{x}} =\mathrm{18}{n}+\mathrm{13}=\frac{\mathrm{18}×\left(\mathrm{7}{m}+\mathrm{1}\right)+\mathrm{52}}{\mathrm{4}}=\frac{\mathrm{7}\left(\mathrm{9}{m}+\mathrm{5}\right)}{\mathrm{2}} \\ $$$$\frac{\mathrm{9}{m}+\mathrm{5}}{\mathrm{2}}=\mathrm{7}^{{i}} \\ $$$${m}=\frac{\mathrm{2}×\mathrm{7}^{{i}} −\mathrm{5}}{\mathrm{9}} \\ $$$${for}\:{m}\:{to}\:{be}\:{integer}\:\Rightarrow{i}=\mathrm{1},\mathrm{4},\mathrm{7}...\:{or}\:\mathrm{3}{k}−\mathrm{2}\:{with}\:{k}\in\mathbb{N}^{+} \\ $$$${i}.{e}.\:{m}=\frac{\mathrm{2}×\mathrm{7}^{\mathrm{3}{k}−\mathrm{2}} −\mathrm{5}}{\mathrm{9}}\:\:\:\:\:\:\:\:\left(\ast\:{see}\:{comment}\right) \\ $$$$\Rightarrow\mathrm{7}^{{x}} =\frac{\mathrm{7}\left(\mathrm{18}{m}+\mathrm{5}\right)}{\mathrm{2}}=\mathrm{7}×\mathrm{7}^{\mathrm{3}{k}−\mathrm{2}} =\mathrm{7}^{\mathrm{3}{k}−\mathrm{1}} \\ $$$$\Rightarrow{Solution}\:{is}\:{x}=\mathrm{3}{k}−\mathrm{1},\:{k}\in\mathbb{N}^{+} \\ $$$${i}.{e}.\:{x}=\mathrm{2},\mathrm{5},\mathrm{8},\mathrm{11}... \\ $$

Commented by mrW1 last updated on 23/May/17

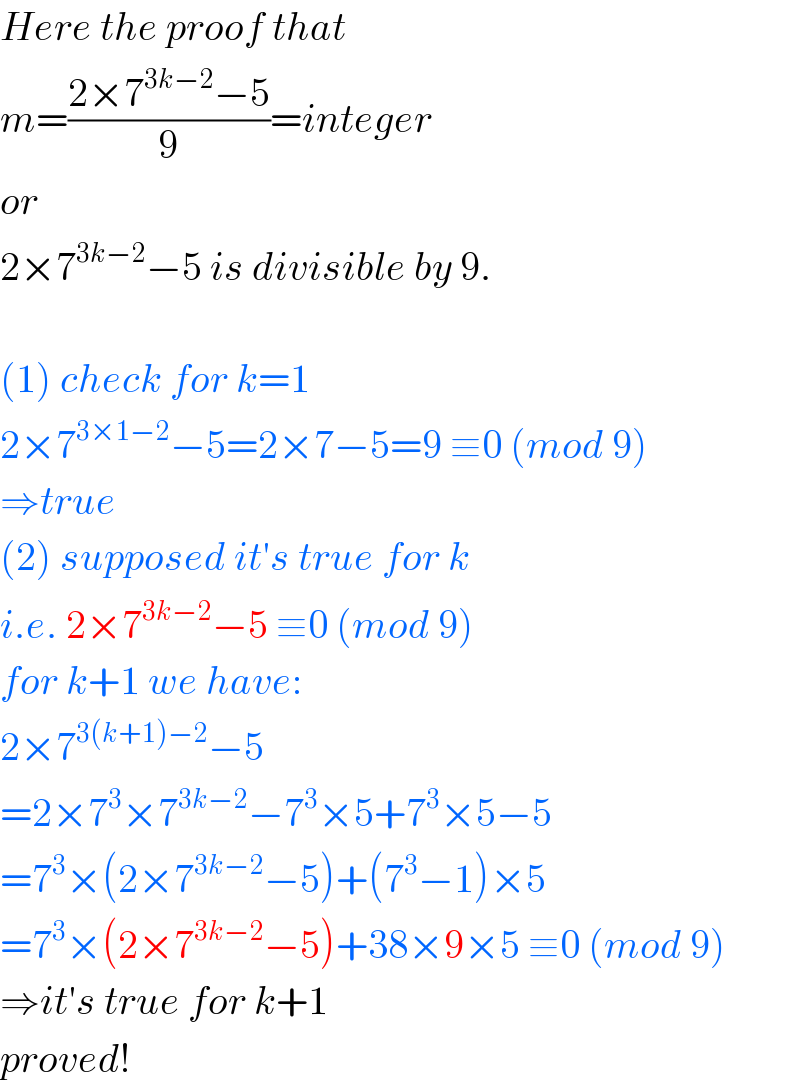
Here the proof that m=((2×7^(3k−2) −5)/9)=integer or 2×7^(3k−2) −5 is divisible by 9. (1) check for k=1 2×7^(3×1−2) −5=2×7−5=9 ≡0 (mod 9) ⇒true (2) supposed it′s true for k i.e. 2×7^(3k−2) −5 ≡0 (mod 9) for k+1 we have: 2×7^(3(k+1)−2) −5 =2×7^3 ×7^(3k−2) −7^3 ×5+7^3 ×5−5 =7^3 ×(2×7^(3k−2) −5)+(7^3 −1)×5 =7^3 ×(2×7^(3k−2) −5)+38×9×5 ≡0 (mod 9) ⇒it′s true for k+1 proved!

$${Here}\:{the}\:{proof}\:{that} \\ $$$${m}=\frac{\mathrm{2}×\mathrm{7}^{\mathrm{3}{k}−\mathrm{2}} −\mathrm{5}}{\mathrm{9}}={integer} \\ $$$${or} \\ $$$$\mathrm{2}×\mathrm{7}^{\mathrm{3}{k}−\mathrm{2}} −\mathrm{5}\:{is}\:{divisible}\:{by}\:\mathrm{9}. \\ $$$$ \\ $$$$\left(\mathrm{1}\right)\:{check}\:{for}\:{k}=\mathrm{1} \\ $$$$\mathrm{2}×\mathrm{7}^{\mathrm{3}×\mathrm{1}−\mathrm{2}} −\mathrm{5}=\mathrm{2}×\mathrm{7}−\mathrm{5}=\mathrm{9}\:\equiv\mathrm{0}\:\left({mod}\:\mathrm{9}\right) \\ $$$$\Rightarrow{true} \\ $$$$\left(\mathrm{2}\right)\:{supposed}\:{it}'{s}\:{true}\:{for}\:{k} \\ $$$${i}.{e}.\:\mathrm{2}×\mathrm{7}^{\mathrm{3}{k}−\mathrm{2}} −\mathrm{5}\:\equiv\mathrm{0}\:\left({mod}\:\mathrm{9}\right) \\ $$$${for}\:{k}+\mathrm{1}\:{we}\:{have}: \\ $$$$\mathrm{2}×\mathrm{7}^{\mathrm{3}\left({k}+\mathrm{1}\right)−\mathrm{2}} −\mathrm{5} \\ $$$$=\mathrm{2}×\mathrm{7}^{\mathrm{3}} ×\mathrm{7}^{\mathrm{3}{k}−\mathrm{2}} −\mathrm{7}^{\mathrm{3}} ×\mathrm{5}+\mathrm{7}^{\mathrm{3}} ×\mathrm{5}−\mathrm{5} \\ $$$$=\mathrm{7}^{\mathrm{3}} ×\left(\mathrm{2}×\mathrm{7}^{\mathrm{3}{k}−\mathrm{2}} −\mathrm{5}\right)+\left(\mathrm{7}^{\mathrm{3}} −\mathrm{1}\right)×\mathrm{5} \\ $$$$=\mathrm{7}^{\mathrm{3}} ×\left(\mathrm{2}×\mathrm{7}^{\mathrm{3}{k}−\mathrm{2}} −\mathrm{5}\right)+\mathrm{38}×\mathrm{9}×\mathrm{5}\:\equiv\mathrm{0}\:\left({mod}\:\mathrm{9}\right) \\ $$$$\Rightarrow{it}'{s}\:{true}\:{for}\:{k}+\mathrm{1} \\ $$$${proved}! \\ $$

Commented by AH Soomro last updated on 24/May/17

Thanks.

$${Thanks}. \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com