
Question and Answers Forum
Question Number 137829 by mnjuly1970 last updated on 07/Apr/21
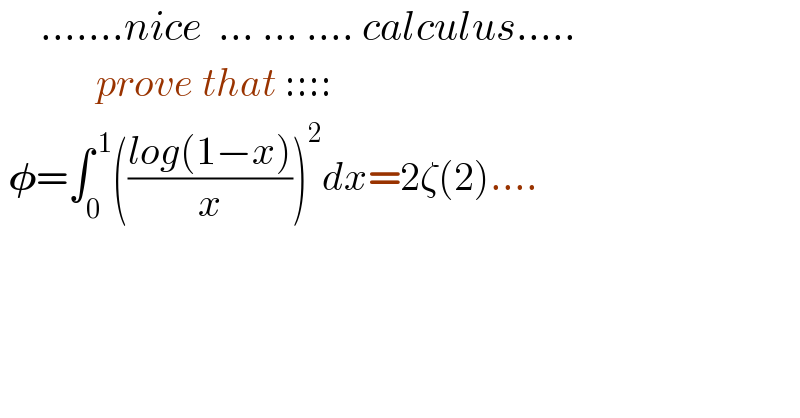
Answered by EnterUsername last updated on 07/Apr/21
![∫_0 ^1 (((ln(1−x))/x))^2 dx =∫_0 ^1 ((ln^2 x)/((1−x)^2 ))dx=[((ln^2 x)/(1−x))−2∫((lnx)/(x(1−x)))dx]_0 ^1 =[((ln^2 x)/(1−x))−2∫(((lnx)/x)+((lnx)/(1−x)))dx]_0 ^1 =[((ln^2 x)/(1−x))−ln^2 x]_0 ^1 −2∫_0 ^1 ((lnx)/(1−x))dx =2ψ′(1)=2Σ_(n=0) ^∞ (1/((n+1)^2 ))=2Σ_(n=1) ^∞ (1/n^2 )=2ζ(2)=(π^2 /3)](Q137831.png)
Commented by mnjuly1970 last updated on 07/Apr/21

| ||
Question and Answers Forum | ||
Question Number 137829 by mnjuly1970 last updated on 07/Apr/21 | ||
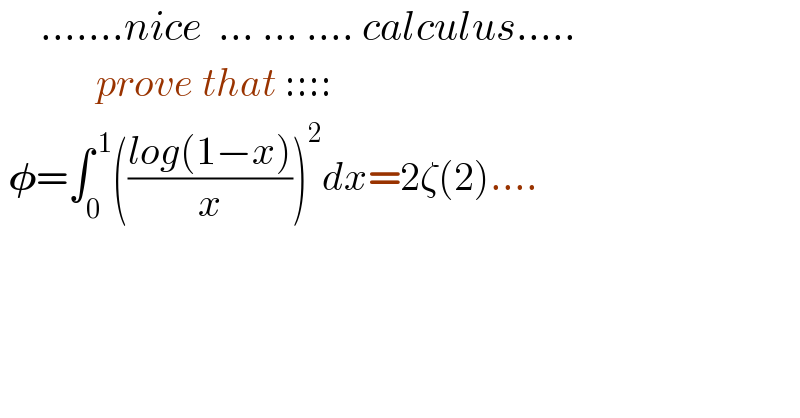 | ||
Answered by EnterUsername last updated on 07/Apr/21 | ||
![∫_0 ^1 (((ln(1−x))/x))^2 dx =∫_0 ^1 ((ln^2 x)/((1−x)^2 ))dx=[((ln^2 x)/(1−x))−2∫((lnx)/(x(1−x)))dx]_0 ^1 =[((ln^2 x)/(1−x))−2∫(((lnx)/x)+((lnx)/(1−x)))dx]_0 ^1 =[((ln^2 x)/(1−x))−ln^2 x]_0 ^1 −2∫_0 ^1 ((lnx)/(1−x))dx =2ψ′(1)=2Σ_(n=0) ^∞ (1/((n+1)^2 ))=2Σ_(n=1) ^∞ (1/n^2 )=2ζ(2)=(π^2 /3)](Q137831.png) | ||
| ||
Commented by mnjuly1970 last updated on 07/Apr/21 | ||
 | ||