
Question and Answers Forum
Question Number 138041 by mnjuly1970 last updated on 09/Apr/21
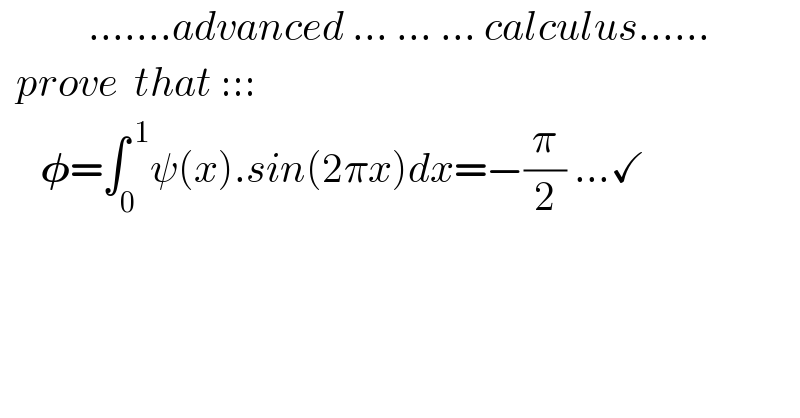
Answered by Dwaipayan Shikari last updated on 09/Apr/21
![∫_0 ^1 ψ(x)sin(2πx)dx =[sin(2πx)log(Γ(x))]_0 ^1 −2π∫_0 ^1 log(Γ(x))cos(2πx) =−π∫_0 ^1 log(π)cos(2πx)+π∫_0 ^1 log(sin(πx))cos(2πx)dx =∫_0 ^π log(sin(u))cos(2u)du =[(1/2)log(sin(u))sin(2u)]_0 ^π −(1/2)∫_0 ^π ((sin(2u)cos(u))/(sin(u)))du =−(1/2)∫_0 ^π 1+cos(2u)du=−(π/2)](Q138052.png)
Commented by mnjuly1970 last updated on 09/Apr/21
Answered by mnjuly1970 last updated on 09/Apr/21
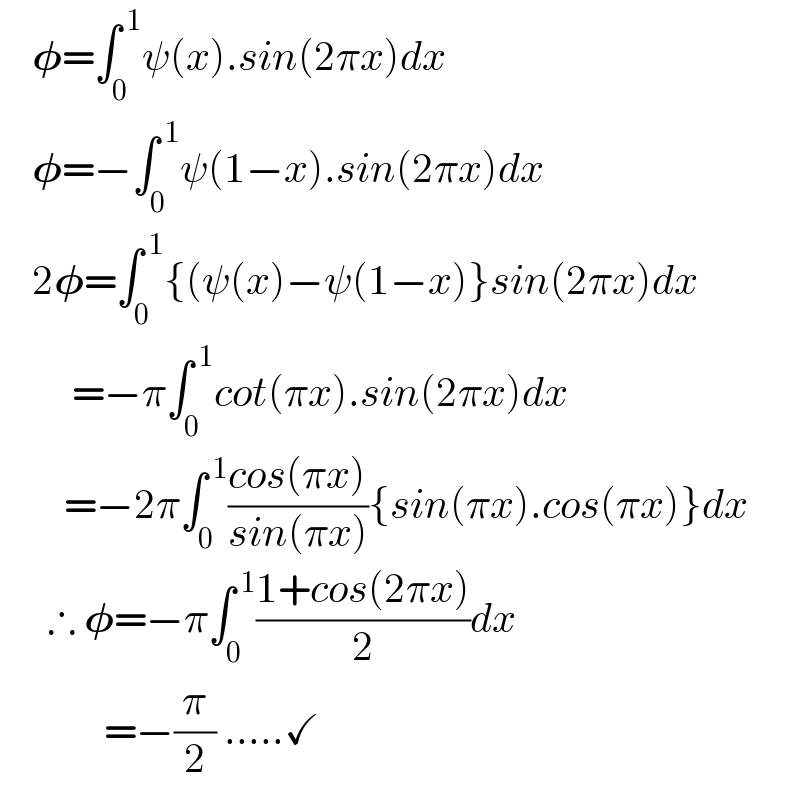
| ||
Question and Answers Forum | ||
Question Number 138041 by mnjuly1970 last updated on 09/Apr/21 | ||
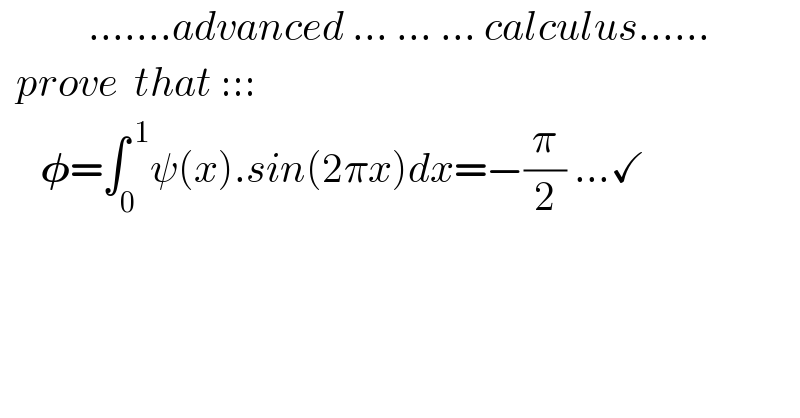 | ||
Answered by Dwaipayan Shikari last updated on 09/Apr/21 | ||
![∫_0 ^1 ψ(x)sin(2πx)dx =[sin(2πx)log(Γ(x))]_0 ^1 −2π∫_0 ^1 log(Γ(x))cos(2πx) =−π∫_0 ^1 log(π)cos(2πx)+π∫_0 ^1 log(sin(πx))cos(2πx)dx =∫_0 ^π log(sin(u))cos(2u)du =[(1/2)log(sin(u))sin(2u)]_0 ^π −(1/2)∫_0 ^π ((sin(2u)cos(u))/(sin(u)))du =−(1/2)∫_0 ^π 1+cos(2u)du=−(π/2)](Q138052.png) | ||
| ||
Commented by mnjuly1970 last updated on 09/Apr/21 | ||
 | ||
Answered by mnjuly1970 last updated on 09/Apr/21 | ||
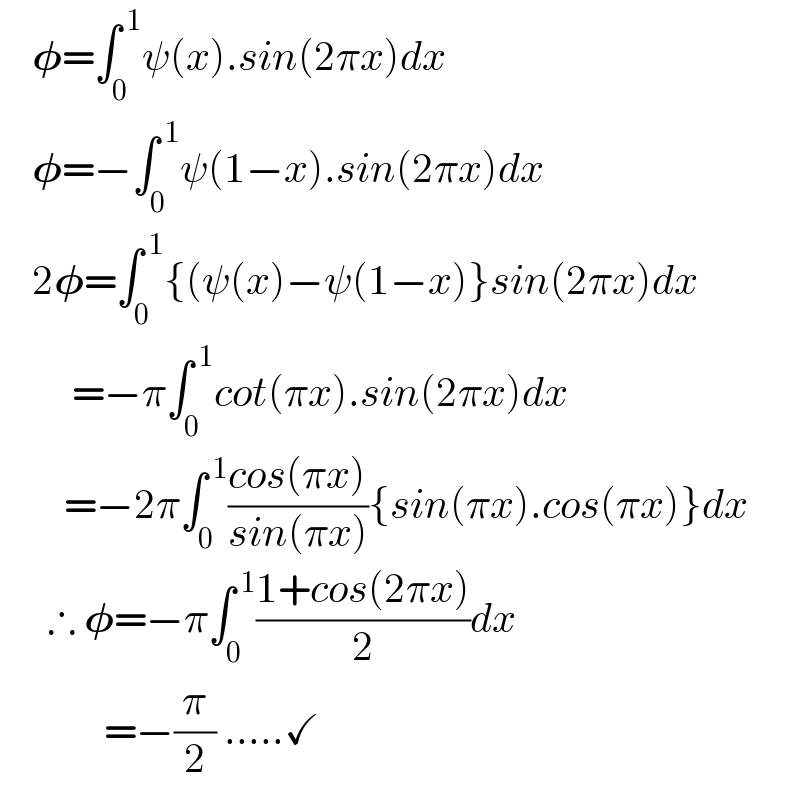 | ||
| ||