
Question and Answers Forum
Question Number 138112 by 676597498 last updated on 10/Apr/21
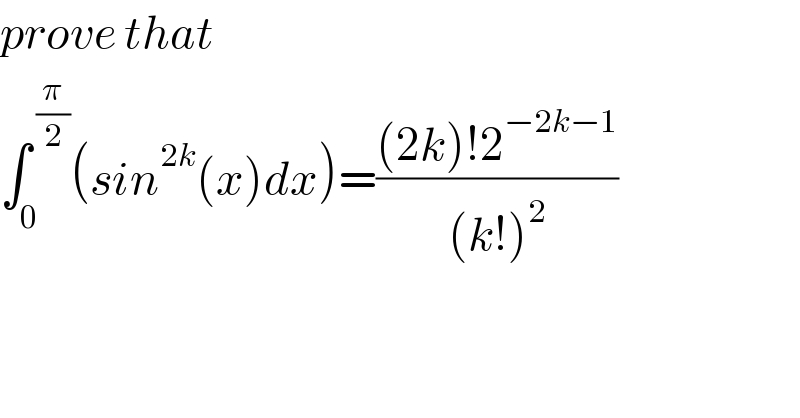
Answered by Dwaipayan Shikari last updated on 10/Apr/21
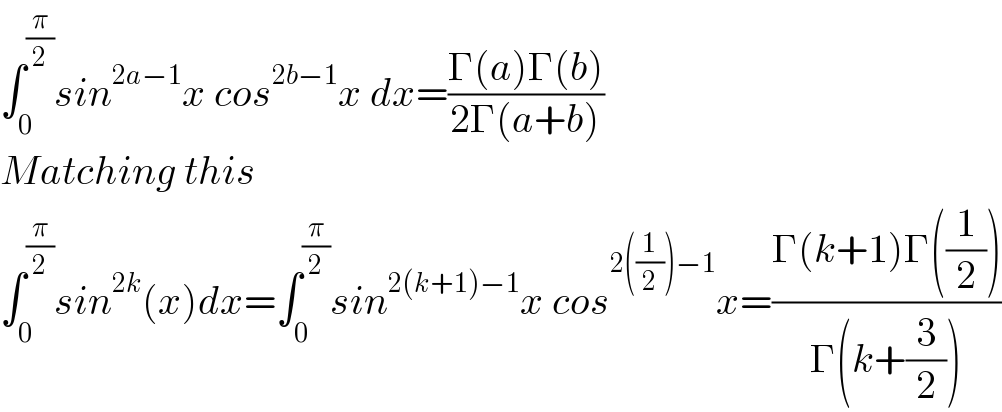
Answered by mathmax by abdo last updated on 10/Apr/21
![let I_n =∫_0 ^(π/2) sin^n xdx ⇒I_n =∫_0 ^(π/2) sin^(n−2) x (1−cos^2 x)dx =∫_0 ^(π/2) sin^(n−2) xdx−∫_0 ^(π/2) cos^2 x sin^(n−2) xdx we[have ∫_0 ^(π/2) sin^(n−2) xdx=I_(n−2) and by recurrence ∫_0 ^(π/2) cosx (cosx sin^(n−2) x)dx =[((sin^(n−1) x)/(n−1))cosx]_0 ^(π/2) +∫_0 ^(π/2) sinx ((sin^(n−1) x)/(n−1))dx =(1/(n−1))I_n ⇒I_n =I_(n−2) −(1/(n−1))I_n ⇒(1+(1/(n−1)))I_n =I_(n−2) ⇒ (n/(n−1))I_n =I_(n−2) ⇒I_n =((n−1)/n) I_(n−2) ⇒ I_(2n) =((2n−1)/(2n))I_(2n−2) (n≥1) ⇒Π_(k=1) ^(n ) I_(2k) =Π_(k=1) ^n ((2k−1)/(2k)) I_(2k−2) ⇒ I_2 .I_4 ......I_(2n) =((Π_(k=1) ^n (2k−1))/(2^n n!)) I_0 .I_2 .....I_(2n−2) ⇒ I_(2n) =((1.3.5....(2n−1))/(2^n .n!)) I_0 =(π/2) ((1.2.3.4.5.....(2n−1)(2n))/(2^n n! .2^(n .) n!)) =(π/2)×(((2n)!)/(2^(2n) (n!)^2 )) ⇒∫_0 ^(π/2) sin^(2n) xdx =((π(2n)!)/(2^(2n+1) (n!)^2 ))](Q138127.png)
| ||
Question and Answers Forum | ||
Question Number 138112 by 676597498 last updated on 10/Apr/21 | ||
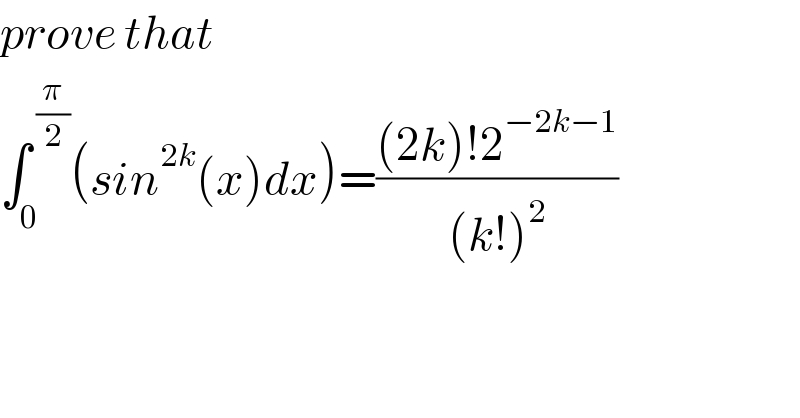 | ||
Answered by Dwaipayan Shikari last updated on 10/Apr/21 | ||
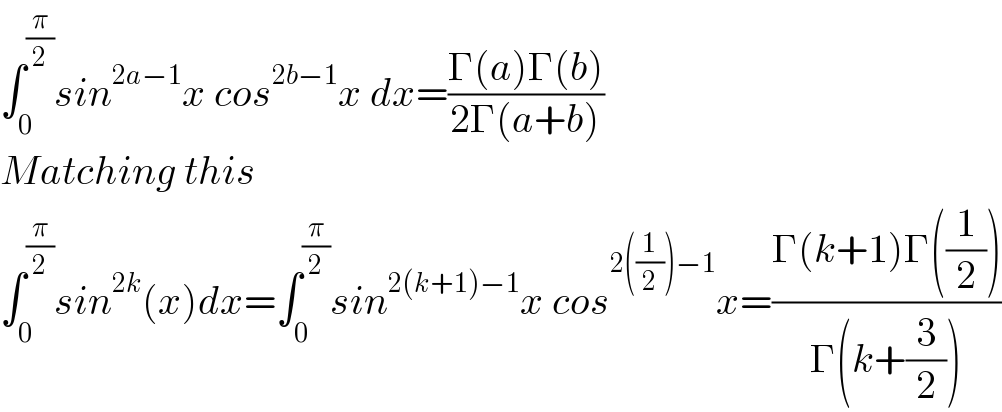 | ||
| ||
Answered by mathmax by abdo last updated on 10/Apr/21 | ||
![let I_n =∫_0 ^(π/2) sin^n xdx ⇒I_n =∫_0 ^(π/2) sin^(n−2) x (1−cos^2 x)dx =∫_0 ^(π/2) sin^(n−2) xdx−∫_0 ^(π/2) cos^2 x sin^(n−2) xdx we[have ∫_0 ^(π/2) sin^(n−2) xdx=I_(n−2) and by recurrence ∫_0 ^(π/2) cosx (cosx sin^(n−2) x)dx =[((sin^(n−1) x)/(n−1))cosx]_0 ^(π/2) +∫_0 ^(π/2) sinx ((sin^(n−1) x)/(n−1))dx =(1/(n−1))I_n ⇒I_n =I_(n−2) −(1/(n−1))I_n ⇒(1+(1/(n−1)))I_n =I_(n−2) ⇒ (n/(n−1))I_n =I_(n−2) ⇒I_n =((n−1)/n) I_(n−2) ⇒ I_(2n) =((2n−1)/(2n))I_(2n−2) (n≥1) ⇒Π_(k=1) ^(n ) I_(2k) =Π_(k=1) ^n ((2k−1)/(2k)) I_(2k−2) ⇒ I_2 .I_4 ......I_(2n) =((Π_(k=1) ^n (2k−1))/(2^n n!)) I_0 .I_2 .....I_(2n−2) ⇒ I_(2n) =((1.3.5....(2n−1))/(2^n .n!)) I_0 =(π/2) ((1.2.3.4.5.....(2n−1)(2n))/(2^n n! .2^(n .) n!)) =(π/2)×(((2n)!)/(2^(2n) (n!)^2 )) ⇒∫_0 ^(π/2) sin^(2n) xdx =((π(2n)!)/(2^(2n+1) (n!)^2 ))](Q138127.png) | ||
| ||