Question and Answers Forum

All Questions      Topic List

Integration Questions

Previous in All Question      Next in All Question      

Previous in Integration      Next in Integration      

Question Number 138710 by bramlexs22 last updated on 17/Apr/21

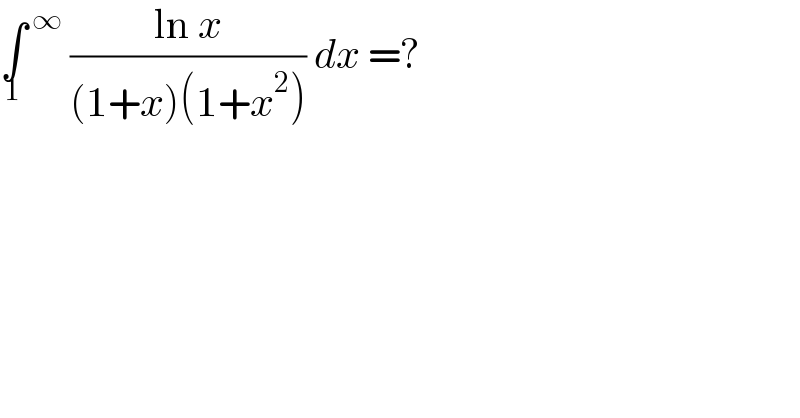
∫^( ∞) _1 ((ln x)/((1+x)(1+x^2 ))) dx =?

$$\underset{\mathrm{1}} {\int}^{\:\infty} \:\frac{\mathrm{ln}\:{x}}{\left(\mathrm{1}+{x}\right)\left(\mathrm{1}+{x}^{\mathrm{2}} \right)}\:{dx}\:=? \\ $$

Answered by mathmax by abdo last updated on 17/Apr/21

Φ=∫_1 ^∞ ((logx)/((1+x)(1+x^2 )))dx ⇒Φ=_(x=(1/t)) −∫_0 ^1 ((−logt)/((1+(1/t))(1+(1/t^2 ))))(−(dt/t^2 )) =−∫_0 ^1 ((tlogt)/((t+1)(t^2 +1)))dt =−∫_0 ^1 (((t+1−1)logt)/((t+1)(t^2 +1)))dt =−∫_0 ^1 ((logt)/(t^2 +1))dt +∫_0 ^1 ((logt)/((t+1)(t^2 +1)))dt we have ∫_0 ^1 ((logt)/(t^2 +1))dt =∫_0 ^1 logtΣ_(n0) ^∞ (−1)^n t^(2n) dt =Σ_(n=0) ^∞ (−1)^n ∫_0 ^1 t^(2n) logt dt =Σ_(n=0) ^∞ (−1)^n u_n u_n =[(t^(2n+1) /(2n+1))logt]_0 ^1 −∫_0 ^1 (t^(2n) /(2n+1))dt =−(1/((2n+1)^2 )) ⇒∫_0 ^1 ((logt)/(t^2 +1))dt =−Σ_(n=0) ^∞ (((−1)^n )/((2n+1)^2 )) =−K(katalan constant) ∫_0 ^1 ((logt)/((t+1)(t^2 +1)))dt =(1/2)∫_0 ^1 ((1/(t+1))−((t−1)/(t^2 +1)))logt dt =(1/2)∫_0 ^1 ((logt)/(t+1))dt −(1/2)∫_0 ^1 (((t−1)logt)/(t^2 +1))dt ∫_0 ^1 ((logt)/(t+1))dt =[log(t+1)logt]_0 ^1 −∫_0 ^1 ((log(t+1))/t)dt we have (d/dt)log(1+t)=(1/(1+t)) =Σ_(n=0) ^∞ (−1)^n t^n ⇒ log(1+t)=Σ_(n=0) ^∞ (−1)^n (t^(n+1) /(n+1))+c(c=0) =Σ_(n=1) ^∞ (((−1)^(n−1) t^n )/n) ⇒ ∫_0 ^1 ((log(1+t))/t)dt =Σ_(n=1) ^∞ ∫_0 ^1 (((−1)^(n−1) t^(n−1) )/n)dt =Σ_(n=1) ^∞ (((−1)^(n−1) )/n^2 ) =−Σ_(n=1) ^∞ (((−1)^n )/n^2 ) =−(2^(1−2) −1)ξ(2) =−((1/2)−1)(π^2 /6) =(π^2 /(12)) ∫_0 ^1 (((t−1)logt)/(t^2 +1))dt =∫_0 ^1 (t−1)logtΣ_(n=0) ^∞ (−1)^n t^(2n) dt =Σ_(n=0) ^∞ (−1)^n ∫_0 ^1 (t^(2n+1) −t^(2n) )logt dt =Σ_(n=0) ^∞ (−1)^n v_n with v_n =∫_0 ^1 (t^(2n+1) −t^(2n) )logt dt =[((t^(2n+2) /(2n+2))−(t^(2n+1) /(2n+1)))logt]_0 ^1 −∫_0 ^1 ((t^(2n+1) /(2n+2))−(t^(2n) /(2n+1)))dt =−(1/((2n+2)^2 ))+(1/((2n+1)^2 )) ⇒ ∫_0 ^1 (((t−1)logt)/(t^2 +1))dt =−Σ_(n=0) ^∞ (((−1)^n )/(4(n+1)^2 ))+Σ_(n=0) ^∞ (((−1)^n )/((2n+1)^2 )) =−(1/4)Σ_(n=1) ^∞ (((−1)^(n−1) )/n^2 )+K =(1/4)Σ_(n=1) ^∞ (((−1)^n )/n^2 )+K =(1/4)(2^(1−2) −1)ξ(2)=(1/4)(−(1/2)).(π^2 /6) =−(π^2 /(48)) rest to collect the values...

$$\Phi=\int_{\mathrm{1}} ^{\infty} \:\frac{\mathrm{logx}}{\left(\mathrm{1}+\mathrm{x}\right)\left(\mathrm{1}+\mathrm{x}^{\mathrm{2}} \right)}\mathrm{dx}\:\Rightarrow\Phi=_{\mathrm{x}=\frac{\mathrm{1}}{\mathrm{t}}} \:−\int_{\mathrm{0}} ^{\mathrm{1}} \:\frac{−\mathrm{logt}}{\left(\mathrm{1}+\frac{\mathrm{1}}{\mathrm{t}}\right)\left(\mathrm{1}+\frac{\mathrm{1}}{\mathrm{t}^{\mathrm{2}} }\right)}\left(−\frac{\mathrm{dt}}{\mathrm{t}^{\mathrm{2}} }\right) \\ $$$$=−\int_{\mathrm{0}} ^{\mathrm{1}} \:\frac{\mathrm{tlogt}}{\left(\mathrm{t}+\mathrm{1}\right)\left(\mathrm{t}^{\mathrm{2}} \:+\mathrm{1}\right)}\mathrm{dt}\:=−\int_{\mathrm{0}} ^{\mathrm{1}} \:\frac{\left(\mathrm{t}+\mathrm{1}−\mathrm{1}\right)\mathrm{logt}}{\left(\mathrm{t}+\mathrm{1}\right)\left(\mathrm{t}^{\mathrm{2}} \:+\mathrm{1}\right)}\mathrm{dt} \\ $$$$=−\int_{\mathrm{0}} ^{\mathrm{1}} \:\frac{\mathrm{logt}}{\mathrm{t}^{\mathrm{2}} \:+\mathrm{1}}\mathrm{dt}\:+\int_{\mathrm{0}} ^{\mathrm{1}} \:\frac{\mathrm{logt}}{\left(\mathrm{t}+\mathrm{1}\right)\left(\mathrm{t}^{\mathrm{2}} +\mathrm{1}\right)}\mathrm{dt}\:\:\mathrm{we}\:\mathrm{have} \\ $$$$\int_{\mathrm{0}} ^{\mathrm{1}} \:\frac{\mathrm{logt}}{\mathrm{t}^{\mathrm{2}} \:+\mathrm{1}}\mathrm{dt}\:=\int_{\mathrm{0}} ^{\mathrm{1}} \:\mathrm{logt}\sum_{\mathrm{n0}} ^{\infty} \:\left(−\mathrm{1}\right)^{\mathrm{n}} \mathrm{t}^{\mathrm{2n}} \mathrm{dt} \\ $$$$=\sum_{\mathrm{n}=\mathrm{0}} ^{\infty} \:\left(−\mathrm{1}\right)^{\mathrm{n}} \int_{\mathrm{0}} ^{\mathrm{1}} \:\:\mathrm{t}^{\mathrm{2n}} \:\mathrm{logt}\:\mathrm{dt}\:=\sum_{\mathrm{n}=\mathrm{0}} ^{\infty} \left(−\mathrm{1}\right)^{\mathrm{n}} \mathrm{u}_{\mathrm{n}} \\ $$$$\mathrm{u}_{\mathrm{n}} =\left[\frac{\mathrm{t}^{\mathrm{2n}+\mathrm{1}} }{\mathrm{2n}+\mathrm{1}}\mathrm{logt}\right]_{\mathrm{0}} ^{\mathrm{1}} −\int_{\mathrm{0}} ^{\mathrm{1}} \:\frac{\mathrm{t}^{\mathrm{2n}} }{\mathrm{2n}+\mathrm{1}}\mathrm{dt} \\ $$$$=−\frac{\mathrm{1}}{\left(\mathrm{2n}+\mathrm{1}\right)^{\mathrm{2}} }\:\Rightarrow\int_{\mathrm{0}} ^{\mathrm{1}} \:\frac{\mathrm{logt}}{\mathrm{t}^{\mathrm{2}} \:+\mathrm{1}}\mathrm{dt}\:=−\sum_{\mathrm{n}=\mathrm{0}} ^{\infty} \:\frac{\left(−\mathrm{1}\right)^{\mathrm{n}} }{\left(\mathrm{2n}+\mathrm{1}\right)^{\mathrm{2}} }\:=−\mathrm{K}\left(\mathrm{katalan}\:\mathrm{constant}\right) \\ $$$$\int_{\mathrm{0}} ^{\mathrm{1}} \:\frac{\mathrm{logt}}{\left(\mathrm{t}+\mathrm{1}\right)\left(\mathrm{t}^{\mathrm{2}} \:+\mathrm{1}\right)}\mathrm{dt}\:=\frac{\mathrm{1}}{\mathrm{2}}\int_{\mathrm{0}} ^{\mathrm{1}} \left(\frac{\mathrm{1}}{\mathrm{t}+\mathrm{1}}−\frac{\mathrm{t}−\mathrm{1}}{\mathrm{t}^{\mathrm{2}} \:+\mathrm{1}}\right)\mathrm{logt}\:\mathrm{dt} \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}}\int_{\mathrm{0}} ^{\mathrm{1}} \:\frac{\mathrm{logt}}{\mathrm{t}+\mathrm{1}}\mathrm{dt}\:−\frac{\mathrm{1}}{\mathrm{2}}\int_{\mathrm{0}} ^{\mathrm{1}} \:\frac{\left(\mathrm{t}−\mathrm{1}\right)\mathrm{logt}}{\mathrm{t}^{\mathrm{2}} \:+\mathrm{1}}\mathrm{dt} \\ $$$$\int_{\mathrm{0}} ^{\mathrm{1}} \:\frac{\mathrm{logt}}{\mathrm{t}+\mathrm{1}}\mathrm{dt}\:=\left[\mathrm{log}\left(\mathrm{t}+\mathrm{1}\right)\mathrm{logt}\right]_{\mathrm{0}} ^{\mathrm{1}} −\int_{\mathrm{0}} ^{\mathrm{1}} \:\frac{\mathrm{log}\left(\mathrm{t}+\mathrm{1}\right)}{\mathrm{t}}\mathrm{dt} \\ $$$$\mathrm{we}\:\mathrm{have}\:\frac{\mathrm{d}}{\mathrm{dt}}\mathrm{log}\left(\mathrm{1}+\mathrm{t}\right)=\frac{\mathrm{1}}{\mathrm{1}+\mathrm{t}}\:=\sum_{\mathrm{n}=\mathrm{0}} ^{\infty} \left(−\mathrm{1}\right)^{\mathrm{n}} \mathrm{t}^{\mathrm{n}} \:\Rightarrow \\ $$$$\mathrm{log}\left(\mathrm{1}+\mathrm{t}\right)=\sum_{\mathrm{n}=\mathrm{0}} ^{\infty} \:\left(−\mathrm{1}\right)^{\mathrm{n}} \:\frac{\mathrm{t}^{\mathrm{n}+\mathrm{1}} }{\mathrm{n}+\mathrm{1}}+\mathrm{c}\left(\mathrm{c}=\mathrm{0}\right)\:=\sum_{\mathrm{n}=\mathrm{1}} ^{\infty} \:\frac{\left(−\mathrm{1}\right)^{\mathrm{n}−\mathrm{1}} \:\mathrm{t}^{\mathrm{n}} }{\mathrm{n}}\:\Rightarrow \\ $$$$\int_{\mathrm{0}} ^{\mathrm{1}} \frac{\mathrm{log}\left(\mathrm{1}+\mathrm{t}\right)}{\mathrm{t}}\mathrm{dt}\:=\sum_{\mathrm{n}=\mathrm{1}} ^{\infty} \int_{\mathrm{0}} ^{\mathrm{1}} \:\frac{\left(−\mathrm{1}\right)^{\mathrm{n}−\mathrm{1}} \mathrm{t}^{\mathrm{n}−\mathrm{1}} \:}{\mathrm{n}}\mathrm{dt} \\ $$$$=\sum_{\mathrm{n}=\mathrm{1}} ^{\infty} \:\frac{\left(−\mathrm{1}\right)^{\mathrm{n}−\mathrm{1}} }{\mathrm{n}^{\mathrm{2}} }\:=−\sum_{\mathrm{n}=\mathrm{1}} ^{\infty} \:\frac{\left(−\mathrm{1}\right)^{\mathrm{n}} }{\mathrm{n}^{\mathrm{2}} }\:=−\left(\mathrm{2}^{\mathrm{1}−\mathrm{2}} −\mathrm{1}\right)\xi\left(\mathrm{2}\right) \\ $$$$=−\left(\frac{\mathrm{1}}{\mathrm{2}}−\mathrm{1}\right)\frac{\pi^{\mathrm{2}} }{\mathrm{6}}\:=\frac{\pi^{\mathrm{2}} }{\mathrm{12}} \\ $$$$\int_{\mathrm{0}} ^{\mathrm{1}} \:\frac{\left(\mathrm{t}−\mathrm{1}\right)\mathrm{logt}}{\mathrm{t}^{\mathrm{2}} \:+\mathrm{1}}\mathrm{dt}\:=\int_{\mathrm{0}} ^{\mathrm{1}} \left(\mathrm{t}−\mathrm{1}\right)\mathrm{logt}\sum_{\mathrm{n}=\mathrm{0}} ^{\infty} \left(−\mathrm{1}\right)^{\mathrm{n}} \:\mathrm{t}^{\mathrm{2n}} \:\mathrm{dt} \\ $$$$=\sum_{\mathrm{n}=\mathrm{0}} ^{\infty} \left(−\mathrm{1}\right)^{\mathrm{n}} \:\int_{\mathrm{0}} ^{\mathrm{1}} \left(\mathrm{t}^{\mathrm{2n}+\mathrm{1}} −\mathrm{t}^{\mathrm{2n}} \right)\mathrm{logt}\:\mathrm{dt} \\ $$$$=\sum_{\mathrm{n}=\mathrm{0}} ^{\infty} \left(−\mathrm{1}\right)^{\mathrm{n}} \mathrm{v}_{\mathrm{n}} \:\:\mathrm{with}\:\mathrm{v}_{\mathrm{n}} =\int_{\mathrm{0}} ^{\mathrm{1}} \left(\mathrm{t}^{\mathrm{2n}+\mathrm{1}} −\mathrm{t}^{\mathrm{2n}} \right)\mathrm{logt}\:\mathrm{dt} \\ $$$$=\left[\left(\frac{\mathrm{t}^{\mathrm{2n}+\mathrm{2}} }{\mathrm{2n}+\mathrm{2}}−\frac{\mathrm{t}^{\mathrm{2n}+\mathrm{1}} }{\mathrm{2n}+\mathrm{1}}\right)\mathrm{logt}\right]_{\mathrm{0}} ^{\mathrm{1}} −\int_{\mathrm{0}} ^{\mathrm{1}} \left(\frac{\mathrm{t}^{\mathrm{2n}+\mathrm{1}} }{\mathrm{2n}+\mathrm{2}}−\frac{\mathrm{t}^{\mathrm{2n}} }{\mathrm{2n}+\mathrm{1}}\right)\mathrm{dt} \\ $$$$=−\frac{\mathrm{1}}{\left(\mathrm{2n}+\mathrm{2}\right)^{\mathrm{2}} }+\frac{\mathrm{1}}{\left(\mathrm{2n}+\mathrm{1}\right)^{\mathrm{2}} }\:\Rightarrow \\ $$$$\int_{\mathrm{0}} ^{\mathrm{1}} \:\frac{\left(\mathrm{t}−\mathrm{1}\right)\mathrm{logt}}{\mathrm{t}^{\mathrm{2}} \:+\mathrm{1}}\mathrm{dt}\:=−\sum_{\mathrm{n}=\mathrm{0}} ^{\infty} \:\frac{\left(−\mathrm{1}\right)^{\mathrm{n}} }{\mathrm{4}\left(\mathrm{n}+\mathrm{1}\right)^{\mathrm{2}} }+\sum_{\mathrm{n}=\mathrm{0}} ^{\infty} \:\frac{\left(−\mathrm{1}\right)^{\mathrm{n}} }{\left(\mathrm{2n}+\mathrm{1}\right)^{\mathrm{2}} } \\ $$$$=−\frac{\mathrm{1}}{\mathrm{4}}\sum_{\mathrm{n}=\mathrm{1}} ^{\infty} \:\frac{\left(−\mathrm{1}\right)^{\mathrm{n}−\mathrm{1}} }{\mathrm{n}^{\mathrm{2}} }+\mathrm{K} \\ $$$$=\frac{\mathrm{1}}{\mathrm{4}}\sum_{\mathrm{n}=\mathrm{1}} ^{\infty} \:\frac{\left(−\mathrm{1}\right)^{\mathrm{n}} }{\mathrm{n}^{\mathrm{2}} }+\mathrm{K}\:=\frac{\mathrm{1}}{\mathrm{4}}\left(\mathrm{2}^{\mathrm{1}−\mathrm{2}} −\mathrm{1}\right)\xi\left(\mathrm{2}\right)=\frac{\mathrm{1}}{\mathrm{4}}\left(−\frac{\mathrm{1}}{\mathrm{2}}\right).\frac{\pi^{\mathrm{2}} }{\mathrm{6}} \\ $$$$=−\frac{\pi^{\mathrm{2}} }{\mathrm{48}}\:\:\:\mathrm{rest}\:\mathrm{to}\:\mathrm{collect}\:\mathrm{the}\:\mathrm{values}... \\ $$

Answered by Kamel last updated on 17/Apr/21

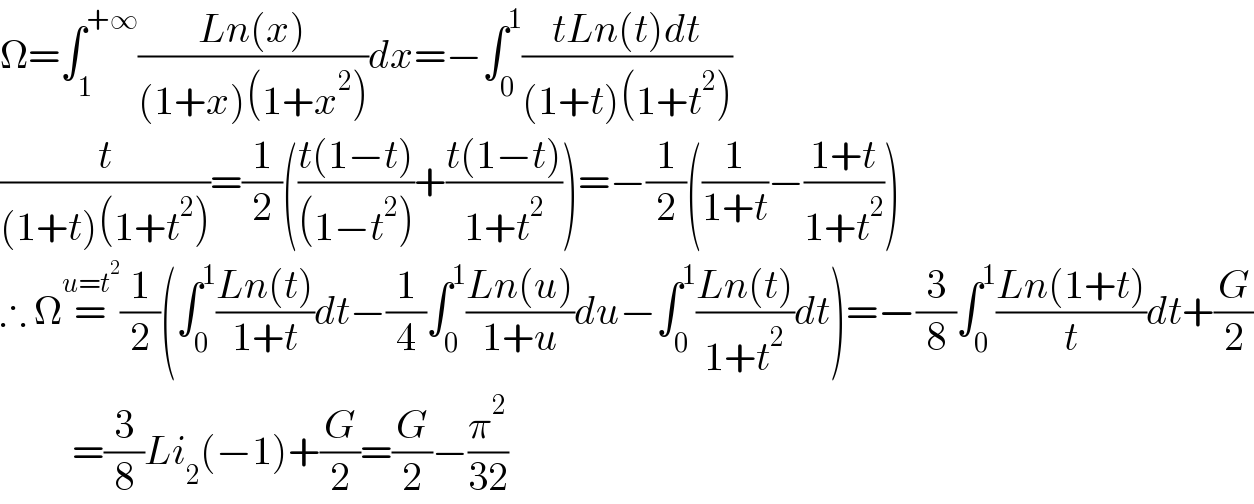
Ω=∫_1 ^(+∞) ((Ln(x))/((1+x)(1+x^2 )))dx=−∫_0 ^1 ((tLn(t)dt)/((1+t)(1+t^2 ))) (t/((1+t)(1+t^2 )))=(1/2)(((t(1−t))/((1−t^2 )))+((t(1−t))/(1+t^2 )))=−(1/2)((1/(1+t))−((1+t)/(1+t^2 ))) ∴ Ω=^(u=t^2 ) (1/2)(∫_0 ^1 ((Ln(t))/(1+t))dt−(1/4)∫_0 ^1 ((Ln(u))/(1+u))du−∫_0 ^1 ((Ln(t))/(1+t^2 ))dt)=−(3/8)∫_0 ^1 ((Ln(1+t))/t)dt+(G/2) =(3/8)Li_2 (−1)+(G/2)=(G/2)−(π^2 /(32))

$$\Omega=\int_{\mathrm{1}} ^{+\infty} \frac{{Ln}\left({x}\right)}{\left(\mathrm{1}+{x}\right)\left(\mathrm{1}+{x}^{\mathrm{2}} \right)}{dx}=−\int_{\mathrm{0}} ^{\mathrm{1}} \frac{{tLn}\left({t}\right){dt}}{\left(\mathrm{1}+{t}\right)\left(\mathrm{1}+{t}^{\mathrm{2}} \right)} \\ $$$$\frac{{t}}{\left(\mathrm{1}+{t}\right)\left(\mathrm{1}+{t}^{\mathrm{2}} \right)}=\frac{\mathrm{1}}{\mathrm{2}}\left(\frac{{t}\left(\mathrm{1}−{t}\right)}{\left(\mathrm{1}−{t}^{\mathrm{2}} \right)}+\frac{{t}\left(\mathrm{1}−{t}\right)}{\mathrm{1}+{t}^{\mathrm{2}} }\right)=−\frac{\mathrm{1}}{\mathrm{2}}\left(\frac{\mathrm{1}}{\mathrm{1}+{t}}−\frac{\mathrm{1}+{t}}{\mathrm{1}+{t}^{\mathrm{2}} }\right) \\ $$$$\therefore\:\Omega\overset{{u}={t}^{\mathrm{2}} } {=}\frac{\mathrm{1}}{\mathrm{2}}\left(\int_{\mathrm{0}} ^{\mathrm{1}} \frac{{Ln}\left({t}\right)}{\mathrm{1}+{t}}{dt}−\frac{\mathrm{1}}{\mathrm{4}}\int_{\mathrm{0}} ^{\mathrm{1}} \frac{{Ln}\left({u}\right)}{\mathrm{1}+{u}}{du}−\int_{\mathrm{0}} ^{\mathrm{1}} \frac{{Ln}\left({t}\right)}{\mathrm{1}+{t}^{\mathrm{2}} }{dt}\right)=−\frac{\mathrm{3}}{\mathrm{8}}\int_{\mathrm{0}} ^{\mathrm{1}} \frac{{Ln}\left(\mathrm{1}+{t}\right)}{{t}}{dt}+\frac{{G}}{\mathrm{2}} \\ $$$$\:\:\:\:\:\:\:\:\:=\frac{\mathrm{3}}{\mathrm{8}}{Li}_{\mathrm{2}} \left(−\mathrm{1}\right)+\frac{{G}}{\mathrm{2}}=\frac{{G}}{\mathrm{2}}−\frac{\pi^{\mathrm{2}} }{\mathrm{32}} \\ $$

Answered by qaz last updated on 17/Apr/21

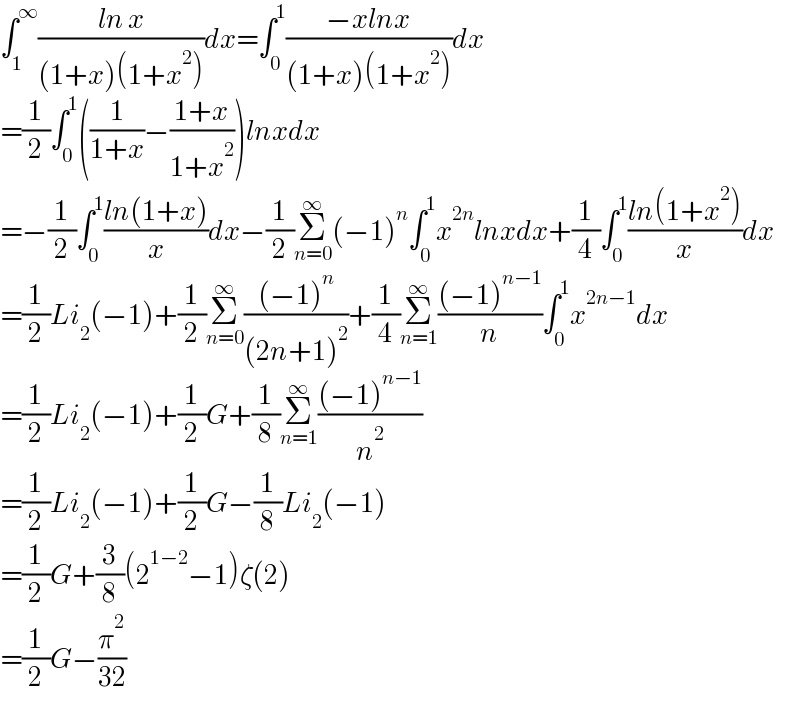
∫_1 ^∞ ((ln x)/((1+x)(1+x^2 )))dx=∫_0 ^1 ((−xlnx)/((1+x)(1+x^2 )))dx =(1/2)∫_0 ^1 ((1/(1+x))−((1+x)/(1+x^2 )))lnxdx =−(1/2)∫_0 ^1 ((ln(1+x))/x)dx−(1/2)Σ_(n=0) ^∞ (−1)^n ∫_0 ^1 x^(2n) lnxdx+(1/4)∫_0 ^1 ((ln(1+x^2 ))/x)dx =(1/2)Li_2 (−1)+(1/2)Σ_(n=0) ^∞ (((−1)^n )/((2n+1)^2 ))+(1/4)Σ_(n=1) ^∞ (((−1)^(n−1) )/n)∫_0 ^1 x^(2n−1) dx =(1/2)Li_2 (−1)+(1/2)G+(1/8)Σ_(n=1) ^∞ (((−1)^(n−1) )/n^2 ) =(1/2)Li_2 (−1)+(1/2)G−(1/8)Li_2 (−1) =(1/2)G+(3/8)(2^(1−2) −1)ζ(2) =(1/2)G−(π^2 /(32))

$$\int_{\mathrm{1}} ^{\infty} \frac{{ln}\:{x}}{\left(\mathrm{1}+{x}\right)\left(\mathrm{1}+{x}^{\mathrm{2}} \right)}{dx}=\int_{\mathrm{0}} ^{\mathrm{1}} \frac{−{xlnx}}{\left(\mathrm{1}+{x}\right)\left(\mathrm{1}+{x}^{\mathrm{2}} \right)}{dx} \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}}\int_{\mathrm{0}} ^{\mathrm{1}} \left(\frac{\mathrm{1}}{\mathrm{1}+{x}}−\frac{\mathrm{1}+{x}}{\mathrm{1}+{x}^{\mathrm{2}} }\right){lnxdx} \\ $$$$=−\frac{\mathrm{1}}{\mathrm{2}}\int_{\mathrm{0}} ^{\mathrm{1}} \frac{{ln}\left(\mathrm{1}+{x}\right)}{{x}}{dx}−\frac{\mathrm{1}}{\mathrm{2}}\underset{{n}=\mathrm{0}} {\overset{\infty} {\sum}}\left(−\mathrm{1}\right)^{{n}} \int_{\mathrm{0}} ^{\mathrm{1}} {x}^{\mathrm{2}{n}} {lnxdx}+\frac{\mathrm{1}}{\mathrm{4}}\int_{\mathrm{0}} ^{\mathrm{1}} \frac{{ln}\left(\mathrm{1}+{x}^{\mathrm{2}} \right)}{{x}}{dx} \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}}{Li}_{\mathrm{2}} \left(−\mathrm{1}\right)+\frac{\mathrm{1}}{\mathrm{2}}\underset{{n}=\mathrm{0}} {\overset{\infty} {\sum}}\frac{\left(−\mathrm{1}\right)^{{n}} }{\left(\mathrm{2}{n}+\mathrm{1}\right)^{\mathrm{2}} }+\frac{\mathrm{1}}{\mathrm{4}}\underset{{n}=\mathrm{1}} {\overset{\infty} {\sum}}\frac{\left(−\mathrm{1}\right)^{{n}−\mathrm{1}} }{{n}}\int_{\mathrm{0}} ^{\mathrm{1}} {x}^{\mathrm{2}{n}−\mathrm{1}} {dx} \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}}{Li}_{\mathrm{2}} \left(−\mathrm{1}\right)+\frac{\mathrm{1}}{\mathrm{2}}{G}+\frac{\mathrm{1}}{\mathrm{8}}\underset{{n}=\mathrm{1}} {\overset{\infty} {\sum}}\frac{\left(−\mathrm{1}\right)^{{n}−\mathrm{1}} }{{n}^{\mathrm{2}} } \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}}{Li}_{\mathrm{2}} \left(−\mathrm{1}\right)+\frac{\mathrm{1}}{\mathrm{2}}{G}−\frac{\mathrm{1}}{\mathrm{8}}{Li}_{\mathrm{2}} \left(−\mathrm{1}\right) \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}}{G}+\frac{\mathrm{3}}{\mathrm{8}}\left(\mathrm{2}^{\mathrm{1}−\mathrm{2}} −\mathrm{1}\right)\zeta\left(\mathrm{2}\right) \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}}{G}−\frac{\pi^{\mathrm{2}} }{\mathrm{32}} \\ $$

Answered by Ar Brandon last updated on 17/Apr/21

Ω=∫_1 ^∞ ((lnx)/((1+x)(1+x^2 )))dx , x=(1/t) =∫_1 ^0 ((ln((1/t)))/((1+(1/t))(1+(1/t^2 ))))∙(−(dt/t^2 ))=−∫_0 ^1 ((tlnt)/((1+t)(1+t^2 )))dt (t/((t+1)(t^2 +1)))=(a/(t+1))+((bt+c)/(t^2 +1))=((a(t^2 +1)+(bt+c)(t+1))/((t+1)(t^2 +1))) a=−(1/2) , a+b=0 , b=(1/2), a+c=0, c=(1/2) (t/((t+1)(t^2 +1)))=−(1/(2(1+t)))+((1+t)/(2(1+t^2 ))) Ω=(1/2)∫_0 ^1 ((lnt)/(1+t))dt−(1/2)∫_0 ^1 ((lnt)/(1+t^2 ))dt−(1/2)∫_0 ^1 ((tlnt)/(1+t^2 ))dt =(1/2)∫_0 ^1 (((1−t)lnt)/(1−t^2 ))dt−(1/2)∫_0 ^(π/4) ln(tanθ)dθ−(1/8)∫_0 ^1 ((ln(u))/(1+u))du =(1/8)∫_0 ^1 (((v^(−(1/2)) −1)ln(v))/(1−v))dv+(G/2)−(1/8)∫_0 ^1 (((1−u)ln(u))/(1−u^2 ))du =(1/8)∫_0 ^1 (((v^(−(1/2)) −1)ln(v))/(1−v))dv+(G/2)−(1/(32))∫_0 ^1 (((p^(−(1/2)) −1)ln(p))/(1−p))dp =(1/8){ψ′(1)−ψ′((1/2))}+(G/2)−(1/(32)){ψ′(1)−ψ′((1/2))} =(1/8)(ζ(2)−3ζ(2))+(G/2)−(1/(32))(ζ(2)−3ζ(2)) =(G/2)+(3/(32))((π^2 /6)−(π^2 /2))=(G/2)−(π^2 /(32))

$$\Omega=\int_{\mathrm{1}} ^{\infty} \frac{\mathrm{lnx}}{\left(\mathrm{1}+\mathrm{x}\right)\left(\mathrm{1}+\mathrm{x}^{\mathrm{2}} \right)}\mathrm{dx}\:,\:\mathrm{x}=\frac{\mathrm{1}}{\mathrm{t}} \\ $$$$\:\:\:\:=\int_{\mathrm{1}} ^{\mathrm{0}} \frac{\mathrm{ln}\left(\frac{\mathrm{1}}{\mathrm{t}}\right)}{\left(\mathrm{1}+\frac{\mathrm{1}}{\mathrm{t}}\right)\left(\mathrm{1}+\frac{\mathrm{1}}{\mathrm{t}^{\mathrm{2}} }\right)}\centerdot\left(−\frac{\mathrm{dt}}{\mathrm{t}^{\mathrm{2}} }\right)=−\int_{\mathrm{0}} ^{\mathrm{1}} \frac{\mathrm{tlnt}}{\left(\mathrm{1}+\mathrm{t}\right)\left(\mathrm{1}+\mathrm{t}^{\mathrm{2}} \right)}\mathrm{dt} \\ $$$$\frac{\mathrm{t}}{\left(\mathrm{t}+\mathrm{1}\right)\left(\mathrm{t}^{\mathrm{2}} +\mathrm{1}\right)}=\frac{\mathrm{a}}{\mathrm{t}+\mathrm{1}}+\frac{\mathrm{bt}+\mathrm{c}}{\mathrm{t}^{\mathrm{2}} +\mathrm{1}}=\frac{\mathrm{a}\left(\mathrm{t}^{\mathrm{2}} +\mathrm{1}\right)+\left(\mathrm{bt}+\mathrm{c}\right)\left(\mathrm{t}+\mathrm{1}\right)}{\left(\mathrm{t}+\mathrm{1}\right)\left(\mathrm{t}^{\mathrm{2}} +\mathrm{1}\right)} \\ $$$$\mathrm{a}=−\frac{\mathrm{1}}{\mathrm{2}}\:,\:\mathrm{a}+\mathrm{b}=\mathrm{0}\:,\:\mathrm{b}=\frac{\mathrm{1}}{\mathrm{2}},\:\mathrm{a}+\mathrm{c}=\mathrm{0},\:\mathrm{c}=\frac{\mathrm{1}}{\mathrm{2}} \\ $$$$\frac{\mathrm{t}}{\left(\mathrm{t}+\mathrm{1}\right)\left(\mathrm{t}^{\mathrm{2}} +\mathrm{1}\right)}=−\frac{\mathrm{1}}{\mathrm{2}\left(\mathrm{1}+\mathrm{t}\right)}+\frac{\mathrm{1}+\mathrm{t}}{\mathrm{2}\left(\mathrm{1}+\mathrm{t}^{\mathrm{2}} \right)} \\ $$$$\Omega=\frac{\mathrm{1}}{\mathrm{2}}\int_{\mathrm{0}} ^{\mathrm{1}} \frac{\mathrm{lnt}}{\mathrm{1}+\mathrm{t}}\mathrm{dt}−\frac{\mathrm{1}}{\mathrm{2}}\int_{\mathrm{0}} ^{\mathrm{1}} \frac{\mathrm{lnt}}{\mathrm{1}+\mathrm{t}^{\mathrm{2}} }\mathrm{dt}−\frac{\mathrm{1}}{\mathrm{2}}\int_{\mathrm{0}} ^{\mathrm{1}} \frac{\mathrm{tlnt}}{\mathrm{1}+\mathrm{t}^{\mathrm{2}} }\mathrm{dt} \\ $$$$\:\:\:\:=\frac{\mathrm{1}}{\mathrm{2}}\int_{\mathrm{0}} ^{\mathrm{1}} \frac{\left(\mathrm{1}−\mathrm{t}\right)\mathrm{lnt}}{\mathrm{1}−\mathrm{t}^{\mathrm{2}} }\mathrm{dt}−\frac{\mathrm{1}}{\mathrm{2}}\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{4}}} \mathrm{ln}\left(\mathrm{tan}\theta\right)\mathrm{d}\theta−\frac{\mathrm{1}}{\mathrm{8}}\int_{\mathrm{0}} ^{\mathrm{1}} \frac{\mathrm{ln}\left(\mathrm{u}\right)}{\mathrm{1}+\mathrm{u}}\mathrm{du} \\ $$$$\:\:\:\:=\frac{\mathrm{1}}{\mathrm{8}}\int_{\mathrm{0}} ^{\mathrm{1}} \frac{\left(\mathrm{v}^{−\frac{\mathrm{1}}{\mathrm{2}}} −\mathrm{1}\right)\mathrm{ln}\left(\mathrm{v}\right)}{\mathrm{1}−\mathrm{v}}\mathrm{dv}+\frac{\mathrm{G}}{\mathrm{2}}−\frac{\mathrm{1}}{\mathrm{8}}\int_{\mathrm{0}} ^{\mathrm{1}} \frac{\left(\mathrm{1}−\mathrm{u}\right)\mathrm{ln}\left(\mathrm{u}\right)}{\mathrm{1}−\mathrm{u}^{\mathrm{2}} }\mathrm{du} \\ $$$$\:\:\:\:=\frac{\mathrm{1}}{\mathrm{8}}\int_{\mathrm{0}} ^{\mathrm{1}} \frac{\left(\mathrm{v}^{−\frac{\mathrm{1}}{\mathrm{2}}} −\mathrm{1}\right)\mathrm{ln}\left(\mathrm{v}\right)}{\mathrm{1}−\mathrm{v}}\mathrm{dv}+\frac{\mathrm{G}}{\mathrm{2}}−\frac{\mathrm{1}}{\mathrm{32}}\int_{\mathrm{0}} ^{\mathrm{1}} \frac{\left(\mathrm{p}^{−\frac{\mathrm{1}}{\mathrm{2}}} −\mathrm{1}\right)\mathrm{ln}\left(\mathrm{p}\right)}{\mathrm{1}−\mathrm{p}}\mathrm{dp} \\ $$$$\:\:\:\:=\frac{\mathrm{1}}{\mathrm{8}}\left\{\psi'\left(\mathrm{1}\right)−\psi'\left(\frac{\mathrm{1}}{\mathrm{2}}\right)\right\}+\frac{\mathrm{G}}{\mathrm{2}}−\frac{\mathrm{1}}{\mathrm{32}}\left\{\psi'\left(\mathrm{1}\right)−\psi'\left(\frac{\mathrm{1}}{\mathrm{2}}\right)\right\} \\ $$$$\:\:\:\:=\frac{\mathrm{1}}{\mathrm{8}}\left(\zeta\left(\mathrm{2}\right)−\mathrm{3}\zeta\left(\mathrm{2}\right)\right)+\frac{\mathrm{G}}{\mathrm{2}}−\frac{\mathrm{1}}{\mathrm{32}}\left(\zeta\left(\mathrm{2}\right)−\mathrm{3}\zeta\left(\mathrm{2}\right)\right) \\ $$$$\:\:\:\:=\frac{\mathrm{G}}{\mathrm{2}}+\frac{\mathrm{3}}{\mathrm{32}}\left(\frac{\pi^{\mathrm{2}} }{\mathrm{6}}−\frac{\pi^{\mathrm{2}} }{\mathrm{2}}\right)=\frac{\mathrm{G}}{\mathrm{2}}−\frac{\pi^{\mathrm{2}} }{\mathrm{32}} \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com