
Question Number 138797 by bramlexs22 last updated on 18/Apr/21
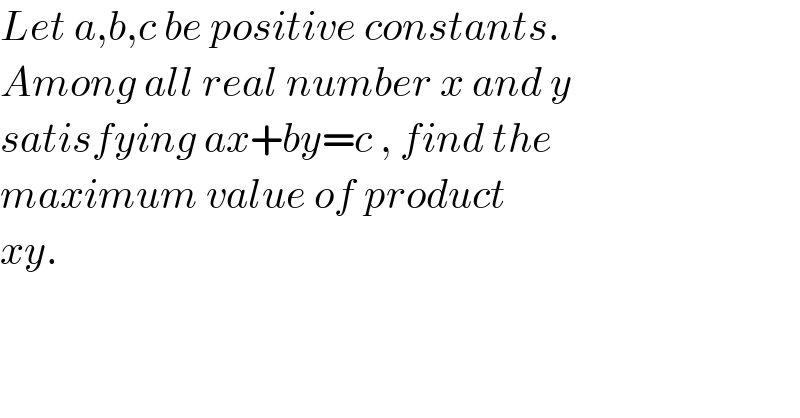
$${Let}\:{a},{b},{c}\:{be}\:{positive}\:{constants}. \\ $$$${Among}\:{all}\:{real}\:{number}\:{x}\:{and}\:{y}\: \\ $$$${satisfying}\:{ax}+{by}={c}\:,\:{find}\:{the} \\ $$$${maximum}\:{value}\:{of}\:{product} \\ $$$${xy}. \\ $$
Answered by TheSupreme last updated on 18/Apr/21

$${if}\:{b}=\mathrm{0}\:{or}\:{a}=\mathrm{0}\:{xy}\:{is}\:{unlimited} \\ $$$${else}:\:{y}=−\frac{{a}}{{b}}{x}−\frac{{c}}{{b}} \\ $$$$\frac{{a}}{{b}}={m}\: \\ $$$$\frac{{c}}{{b}}={q} \\ $$$${y}=−{mx}−{q} \\ $$$$\sigma={xy}={x}\left({mx}+{q}\right)=−{mx}^{\mathrm{2}} −{qx}=−{x}\left({mx}+{q}\right) \\ $$$$\frac{\partial\sigma}{\partial{x}}=−\mathrm{2}{mx}−{q}=\mathrm{0}\:\rightarrow{x}=−\frac{{q}}{\mathrm{2}{m}} \\ $$$$\sigma_{{max}} =\frac{{q}}{\mathrm{2}{m}}\left(\frac{{q}}{\mathrm{2}}\right)=\frac{{q}^{\mathrm{2}} }{\mathrm{4}{m}}=\frac{{c}^{\mathrm{2}} }{\mathrm{4}{ab}} \\ $$
Answered by EDWIN88 last updated on 18/Apr/21

$$\mathrm{without}\:\mathrm{calculus}. \\ $$$$\mathrm{let}\:\begin{cases}{\mathrm{ax}\:=\:\mathrm{u}}\\{\mathrm{by}\:=\:\mathrm{v}}\end{cases}\:\Rightarrow\:\mathrm{u}+\mathrm{v}\:=\:\mathrm{c}\:;\:\mathrm{so}\:\mathrm{u}.\mathrm{v}\:\mathrm{minimum} \\ $$$$\mathrm{where}\:\begin{cases}{\mathrm{u}=\frac{\mathrm{c}}{\mathrm{2}}}\\{\mathrm{v}=\frac{\mathrm{c}}{\mathrm{2}}}\end{cases}\:\mathrm{then}\:\left(\mathrm{uv}\right)_{\mathrm{min}} =\:\frac{\mathrm{c}^{\mathrm{2}} }{\mathrm{4}} \\ $$$$\Rightarrow\left(\mathrm{ax}.\mathrm{by}\right)_{\mathrm{min}} =\:\frac{\mathrm{c}^{\mathrm{2}} }{\mathrm{4}}\:\mathrm{or}\:\mathrm{xy}_{\mathrm{min}} \:=\:\frac{\mathrm{c}^{\mathrm{2}} }{\mathrm{4ab}}.\: \\ $$
