Question and Answers Forum

All Questions      Topic List

Integration Questions

Previous in All Question      Next in All Question      

Previous in Integration      Next in Integration      

Question Number 138819 by qaz last updated on 18/Apr/21

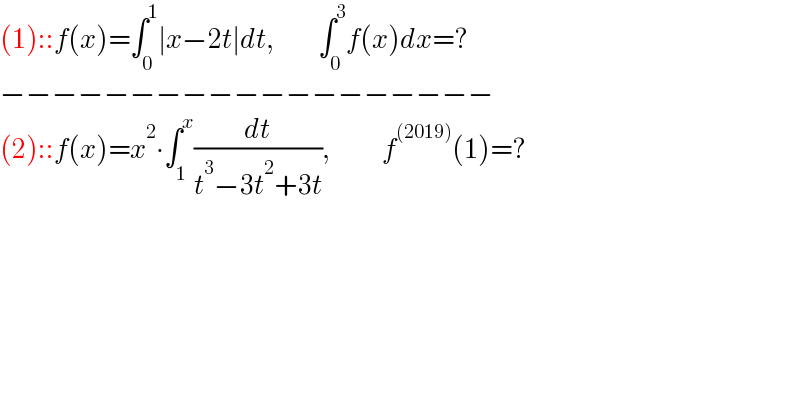
(1)::f(x)=∫_0 ^1 ∣x−2t∣dt, ∫_0 ^3 f(x)dx=? −−−−−−−−−−−−−−−−−−− (2)::f(x)=x^2 ∙∫_1 ^x (dt/(t^3 −3t^2 +3t)), f^((2019)) (1)=?

$$\left(\mathrm{1}\right)::{f}\left({x}\right)=\int_{\mathrm{0}} ^{\mathrm{1}} \mid{x}−\mathrm{2}{t}\mid{dt},\:\:\:\:\:\:\:\:\:\:\:\int_{\mathrm{0}} ^{\mathrm{3}} {f}\left({x}\right){dx}=? \\ $$$$−−−−−−−−−−−−−−−−−−− \\ $$$$\left(\mathrm{2}\right)::{f}\left({x}\right)={x}^{\mathrm{2}} \centerdot\int_{\mathrm{1}} ^{{x}} \frac{{dt}}{{t}^{\mathrm{3}} −\mathrm{3}{t}^{\mathrm{2}} +\mathrm{3}{t}},\:\:\:\:\:\:\:\:\:\:\:\:\:{f}^{\left(\mathrm{2019}\right)} \left(\mathrm{1}\right)=? \\ $$

Answered by TheSupreme last updated on 18/Apr/21

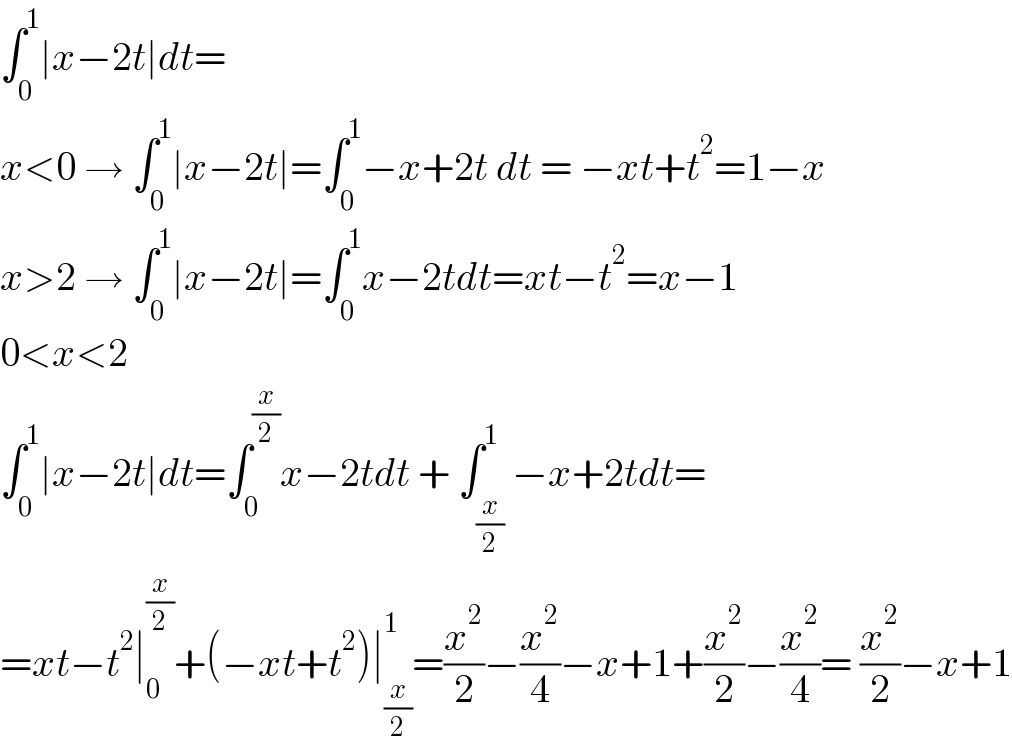
∫_0 ^1 ∣x−2t∣dt= x<0 → ∫_0 ^1 ∣x−2t∣=∫_0 ^1 −x+2t dt = −xt+t^2 =1−x x>2 → ∫_0 ^1 ∣x−2t∣=∫_0 ^1 x−2tdt=xt−t^2 =x−1 0<x<2 ∫_0 ^1 ∣x−2t∣dt=∫_0 ^(x/2) x−2tdt + ∫_(x/2) ^1 −x+2tdt= =xt−t^2 ∣_0 ^(x/2) +(−xt+t^2 )∣_(x/2) ^1 =(x^2 /2)−(x^2 /4)−x+1+(x^2 /2)−(x^2 /4)= (x^2 /2)−x+1

$$\int_{\mathrm{0}} ^{\mathrm{1}} \mid{x}−\mathrm{2}{t}\mid{dt}= \\ $$$${x}<\mathrm{0}\:\rightarrow\:\int_{\mathrm{0}} ^{\mathrm{1}} \mid{x}−\mathrm{2}{t}\mid=\int_{\mathrm{0}} ^{\mathrm{1}} −{x}+\mathrm{2}{t}\:{dt}\:=\:−{xt}+{t}^{\mathrm{2}} =\mathrm{1}−{x} \\ $$$${x}>\mathrm{2}\:\rightarrow\:\int_{\mathrm{0}} ^{\mathrm{1}} \mid{x}−\mathrm{2}{t}\mid=\int_{\mathrm{0}} ^{\mathrm{1}} {x}−\mathrm{2}{tdt}={xt}−{t}^{\mathrm{2}} ={x}−\mathrm{1} \\ $$$$\mathrm{0}<{x}<\mathrm{2} \\ $$$$\int_{\mathrm{0}} ^{\mathrm{1}} \mid{x}−\mathrm{2}{t}\mid{dt}=\int_{\mathrm{0}} ^{\frac{{x}}{\mathrm{2}}} {x}−\mathrm{2}{tdt}\:+\:\int_{\frac{{x}}{\mathrm{2}}} ^{\mathrm{1}} −{x}+\mathrm{2}{tdt}= \\ $$$$={xt}−{t}^{\mathrm{2}} \mid_{\mathrm{0}} ^{\frac{{x}}{\mathrm{2}}} +\left(−{xt}+{t}^{\mathrm{2}} \right)\mid_{\frac{{x}}{\mathrm{2}}} ^{\mathrm{1}} =\frac{{x}^{\mathrm{2}} }{\mathrm{2}}−\frac{{x}^{\mathrm{2}} }{\mathrm{4}}−{x}+\mathrm{1}+\frac{{x}^{\mathrm{2}} }{\mathrm{2}}−\frac{{x}^{\mathrm{2}} }{\mathrm{4}}=\:\frac{{x}^{\mathrm{2}} }{\mathrm{2}}−{x}+\mathrm{1} \\ $$

Answered by mathmax by abdo last updated on 18/Apr/21

f(x)=∫_0 ^1 ∣x−2t∣dt =_(2t=u) (1/2)∫_0 ^2 ∣x−u∣du ⇒2f(x)=∫_0 ^x ∣x−u∣du +∫_x ^2 ∣x−u∣du =∫_0 ^x (x−u)du+∫_x ^2 (u−x)du =[xu−(u^2 /2)]_(u=0) ^x +[(u^2 /2)−xu]_x ^2 =x^2 −(x^2 /2) +2−2x−(x^2 /2)+x^2 =2x^2 −x^2 +2−2x =x^2 −2x+2 ⇒f(x)=(x^2 /2)−x+1 ⇒ ∫_0 ^3 f(x)dx=∫_0 ^3 ((x^2 /2)−x+1)dx =[(x^3 /6)−(x^2 /2)+x]_0 ^3 =((27)/6)−(9/2)+3=...

$$\mathrm{f}\left(\mathrm{x}\right)=\int_{\mathrm{0}} ^{\mathrm{1}} \mid\mathrm{x}−\mathrm{2t}\mid\mathrm{dt}\:=_{\mathrm{2t}=\mathrm{u}} \:\:\:\frac{\mathrm{1}}{\mathrm{2}}\int_{\mathrm{0}} ^{\mathrm{2}} \mid\mathrm{x}−\mathrm{u}\mid\mathrm{du} \\ $$$$\Rightarrow\mathrm{2f}\left(\mathrm{x}\right)=\int_{\mathrm{0}} ^{\mathrm{x}} \mid\mathrm{x}−\mathrm{u}\mid\mathrm{du}\:+\int_{\mathrm{x}} ^{\mathrm{2}} \mid\mathrm{x}−\mathrm{u}\mid\mathrm{du}\:=\int_{\mathrm{0}} ^{\mathrm{x}} \left(\mathrm{x}−\mathrm{u}\right)\mathrm{du}+\int_{\mathrm{x}} ^{\mathrm{2}} \left(\mathrm{u}−\mathrm{x}\right)\mathrm{du} \\ $$$$=\left[\mathrm{xu}−\frac{\mathrm{u}^{\mathrm{2}} }{\mathrm{2}}\right]_{\mathrm{u}=\mathrm{0}} ^{\mathrm{x}} \:+\left[\frac{\mathrm{u}^{\mathrm{2}} }{\mathrm{2}}−\mathrm{xu}\right]_{\mathrm{x}} ^{\mathrm{2}} =\mathrm{x}^{\mathrm{2}} −\frac{\mathrm{x}^{\mathrm{2}} }{\mathrm{2}}\:+\mathrm{2}−\mathrm{2x}−\frac{\mathrm{x}^{\mathrm{2}} }{\mathrm{2}}+\mathrm{x}^{\mathrm{2}} \\ $$$$=\mathrm{2x}^{\mathrm{2}} −\mathrm{x}^{\mathrm{2}} +\mathrm{2}−\mathrm{2x}\:=\mathrm{x}^{\mathrm{2}} −\mathrm{2x}+\mathrm{2}\:\Rightarrow\mathrm{f}\left(\mathrm{x}\right)=\frac{\mathrm{x}^{\mathrm{2}} }{\mathrm{2}}−\mathrm{x}+\mathrm{1}\:\Rightarrow \\ $$$$\int_{\mathrm{0}} ^{\mathrm{3}} \mathrm{f}\left(\mathrm{x}\right)\mathrm{dx}=\int_{\mathrm{0}} ^{\mathrm{3}} \left(\frac{\mathrm{x}^{\mathrm{2}} }{\mathrm{2}}−\mathrm{x}+\mathrm{1}\right)\mathrm{dx}\:=\left[\frac{\mathrm{x}^{\mathrm{3}} }{\mathrm{6}}−\frac{\mathrm{x}^{\mathrm{2}} }{\mathrm{2}}+\mathrm{x}\right]_{\mathrm{0}} ^{\mathrm{3}} =\frac{\mathrm{27}}{\mathrm{6}}−\frac{\mathrm{9}}{\mathrm{2}}+\mathrm{3}=... \\ $$

Answered by mathmax by abdo last updated on 18/Apr/21

f(x)=x^2 ∫_1 ^x (dt/(t(t^2 −3t+3))) let decompose F(t)=(1/(t(t^2 −3t+3))) ⇒F(t)=(a/t)+((bt+c)/(t^2 −3t+3)) we have a=(1/3) lim_(t→+∞) tF(t)=0 =a+b ⇒b=−(1/3) F(1)=1 =a+b+c ⇒c=1−0=1 ⇒F(x)=(1/(3t))+((−(t/3)+1)/(t^2 −3t+3)) ⇒ ∫_1 ^x F(t)dt =∫_1 ^x (dt/(3t))−(1/6)∫_1 ^x ((2t−3−3)/(t^2 −3t+3))dt =(1/3)log∣x∣−(1/6)[log(t^2 −3t+3)]_1 ^x +(3/6)∫_1 ^x (dt/(t^2 −3t+3)) =(1/3)log∣x∣−(1/6)log(x^2 −3x+3)+(3/6)∫_1 ^x (dt/(t^2 −3t+3)) ∫_1 ^x (dt/(t^2 −3t+3)) =∫_1 ^x (dt/(t^2 −2(3/2)t+(9/4)+3−(9/4))) =∫_1 ^x (dt/((t−(3/2))^2 +(3/4)))=_(t−(3/2)=((√3)/2)y) (4/3) ∫_(−(1/( (√3)))) ^((2x−3)/( (√3))) (1/(y^2 +1)).((√3)/2)dy =(2/( (√3)))[arctany]_(−(1/( (√3)))) ^((2x−3)/( (√3))) =(2/( (√3)))(arctan(((2x−3)/( (√3))))+arctan((1/( (√3))))) ⇒∫_1 ^x F(x)dx=(1/3)log∣x∣−(1/6)log(x^2 −3x+3) +(1/( (√3)))(arctan(((2x−3)/( (√3))))+(π/6)) ⇒ f(x)=(1/3)x^2 log∣x∣−(x^2 /6)log(x^2 −3x+3)+(x^2 /( (√3)))(arctan(((2x−3)/( (√3))))+(π/6)) rest to calculate f^((n)) (x)....be continued....

$$\mathrm{f}\left(\mathrm{x}\right)=\mathrm{x}^{\mathrm{2}} \int_{\mathrm{1}} ^{\mathrm{x}} \:\frac{\mathrm{dt}}{\mathrm{t}\left(\mathrm{t}^{\mathrm{2}} −\mathrm{3t}+\mathrm{3}\right)}\:\:\:\mathrm{let}\:\mathrm{decompose}\:\mathrm{F}\left(\mathrm{t}\right)=\frac{\mathrm{1}}{\mathrm{t}\left(\mathrm{t}^{\mathrm{2}} −\mathrm{3t}+\mathrm{3}\right)} \\ $$$$\Rightarrow\mathrm{F}\left(\mathrm{t}\right)=\frac{\mathrm{a}}{\mathrm{t}}+\frac{\mathrm{bt}+\mathrm{c}}{\mathrm{t}^{\mathrm{2}} \:−\mathrm{3t}+\mathrm{3}}\:\:\mathrm{we}\:\mathrm{have}\:\mathrm{a}=\frac{\mathrm{1}}{\mathrm{3}} \\ $$$$\mathrm{lim}_{\mathrm{t}\rightarrow+\infty} \mathrm{tF}\left(\mathrm{t}\right)=\mathrm{0}\:=\mathrm{a}+\mathrm{b}\:\Rightarrow\mathrm{b}=−\frac{\mathrm{1}}{\mathrm{3}} \\ $$$$\mathrm{F}\left(\mathrm{1}\right)=\mathrm{1}\:=\mathrm{a}+\mathrm{b}+\mathrm{c}\:\Rightarrow\mathrm{c}=\mathrm{1}−\mathrm{0}=\mathrm{1}\:\Rightarrow\mathrm{F}\left(\mathrm{x}\right)=\frac{\mathrm{1}}{\mathrm{3t}}+\frac{−\frac{\mathrm{t}}{\mathrm{3}}+\mathrm{1}}{\mathrm{t}^{\mathrm{2}} −\mathrm{3t}+\mathrm{3}}\:\Rightarrow \\ $$$$\int_{\mathrm{1}} ^{\mathrm{x}} \:\mathrm{F}\left(\mathrm{t}\right)\mathrm{dt}\:=\int_{\mathrm{1}} ^{\mathrm{x}} \:\frac{\mathrm{dt}}{\mathrm{3t}}−\frac{\mathrm{1}}{\mathrm{6}}\int_{\mathrm{1}} ^{\mathrm{x}} \:\frac{\mathrm{2t}−\mathrm{3}−\mathrm{3}}{\mathrm{t}^{\mathrm{2}} −\mathrm{3t}+\mathrm{3}}\mathrm{dt} \\ $$$$=\frac{\mathrm{1}}{\mathrm{3}}\mathrm{log}\mid\mathrm{x}\mid−\frac{\mathrm{1}}{\mathrm{6}}\left[\mathrm{log}\left(\mathrm{t}^{\mathrm{2}} −\mathrm{3t}+\mathrm{3}\right)\right]_{\mathrm{1}} ^{\mathrm{x}} +\frac{\mathrm{3}}{\mathrm{6}}\int_{\mathrm{1}} ^{\mathrm{x}} \:\frac{\mathrm{dt}}{\mathrm{t}^{\mathrm{2}} −\mathrm{3t}+\mathrm{3}} \\ $$$$=\frac{\mathrm{1}}{\mathrm{3}}\mathrm{log}\mid\mathrm{x}\mid−\frac{\mathrm{1}}{\mathrm{6}}\mathrm{log}\left(\mathrm{x}^{\mathrm{2}} −\mathrm{3x}+\mathrm{3}\right)+\frac{\mathrm{3}}{\mathrm{6}}\int_{\mathrm{1}} ^{\mathrm{x}} \:\frac{\mathrm{dt}}{\mathrm{t}^{\mathrm{2}} −\mathrm{3t}+\mathrm{3}} \\ $$$$\int_{\mathrm{1}} ^{\mathrm{x}} \:\frac{\mathrm{dt}}{\mathrm{t}^{\mathrm{2}} −\mathrm{3t}+\mathrm{3}}\:=\int_{\mathrm{1}} ^{\mathrm{x}} \frac{\mathrm{dt}}{\mathrm{t}^{\mathrm{2}} −\mathrm{2}\frac{\mathrm{3}}{\mathrm{2}}\mathrm{t}+\frac{\mathrm{9}}{\mathrm{4}}+\mathrm{3}−\frac{\mathrm{9}}{\mathrm{4}}} \\ $$$$=\int_{\mathrm{1}} ^{\mathrm{x}} \:\frac{\mathrm{dt}}{\left(\mathrm{t}−\frac{\mathrm{3}}{\mathrm{2}}\right)^{\mathrm{2}} \:+\frac{\mathrm{3}}{\mathrm{4}}}=_{\mathrm{t}−\frac{\mathrm{3}}{\mathrm{2}}=\frac{\sqrt{\mathrm{3}}}{\mathrm{2}}\mathrm{y}} \frac{\mathrm{4}}{\mathrm{3}}\:\:\int_{−\frac{\mathrm{1}}{\:\sqrt{\mathrm{3}}}} ^{\frac{\mathrm{2x}−\mathrm{3}}{\:\sqrt{\mathrm{3}}}} \:\:\:\:\frac{\mathrm{1}}{\mathrm{y}^{\mathrm{2}} \:+\mathrm{1}}.\frac{\sqrt{\mathrm{3}}}{\mathrm{2}}\mathrm{dy} \\ $$$$=\frac{\mathrm{2}}{\:\sqrt{\mathrm{3}}}\left[\mathrm{arctany}\right]_{−\frac{\mathrm{1}}{\:\sqrt{\mathrm{3}}}} ^{\frac{\mathrm{2x}−\mathrm{3}}{\:\sqrt{\mathrm{3}}}} \:\:\:=\frac{\mathrm{2}}{\:\sqrt{\mathrm{3}}}\left(\mathrm{arctan}\left(\frac{\mathrm{2x}−\mathrm{3}}{\:\sqrt{\mathrm{3}}}\right)+\mathrm{arctan}\left(\frac{\mathrm{1}}{\:\sqrt{\mathrm{3}}}\right)\right) \\ $$$$\Rightarrow\int_{\mathrm{1}} ^{\mathrm{x}} \:\mathrm{F}\left(\mathrm{x}\right)\mathrm{dx}=\frac{\mathrm{1}}{\mathrm{3}}\mathrm{log}\mid\mathrm{x}\mid−\frac{\mathrm{1}}{\mathrm{6}}\mathrm{log}\left(\mathrm{x}^{\mathrm{2}} −\mathrm{3x}+\mathrm{3}\right) \\ $$$$+\frac{\mathrm{1}}{\:\sqrt{\mathrm{3}}}\left(\mathrm{arctan}\left(\frac{\mathrm{2x}−\mathrm{3}}{\:\sqrt{\mathrm{3}}}\right)+\frac{\pi}{\mathrm{6}}\right)\:\Rightarrow \\ $$$$\mathrm{f}\left(\mathrm{x}\right)=\frac{\mathrm{1}}{\mathrm{3}}\mathrm{x}^{\mathrm{2}} \mathrm{log}\mid\mathrm{x}\mid−\frac{\mathrm{x}^{\mathrm{2}} }{\mathrm{6}}\mathrm{log}\left(\mathrm{x}^{\mathrm{2}} −\mathrm{3x}+\mathrm{3}\right)+\frac{\mathrm{x}^{\mathrm{2}} }{\:\sqrt{\mathrm{3}}}\left(\mathrm{arctan}\left(\frac{\mathrm{2x}−\mathrm{3}}{\:\sqrt{\mathrm{3}}}\right)+\frac{\pi}{\mathrm{6}}\right) \\ $$$$\mathrm{rest}\:\mathrm{to}\:\mathrm{calculate}\:\mathrm{f}^{\left(\mathrm{n}\right)} \left(\mathrm{x}\right)....\mathrm{be}\:\mathrm{continued}.... \\ $$

Commented by qaz last updated on 19/Apr/21

it′s just a fill−in−the−blanks exercise, i dont think of that so complicate.

$${it}'{s}\:{just}\:{a}\:{fill}−{in}−{the}−{blanks}\:{exercise}, \\ $$$${i}\:{dont}\:{think}\:{of}\:{that}\:{so}\:{complicate}. \\ $$

Answered by ajfour last updated on 19/Apr/21

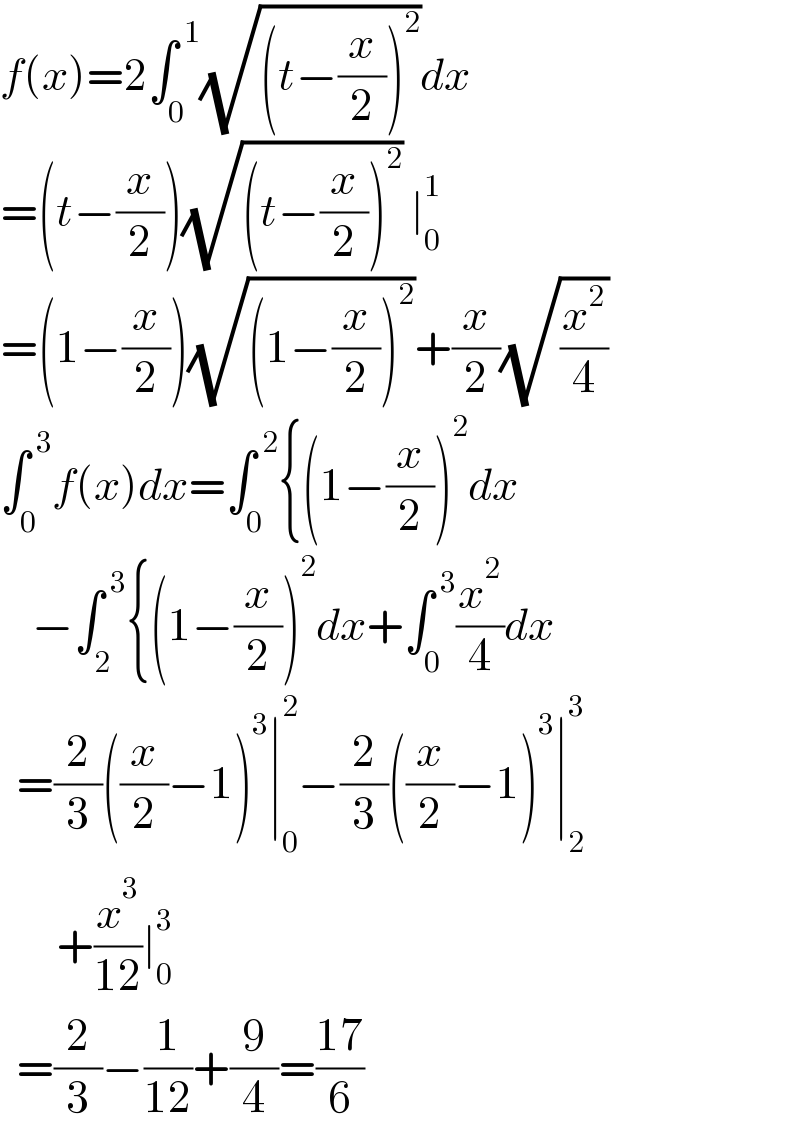
f(x)=2∫_0 ^( 1) (√((t−(x/2))^2 ))dx =(t−(x/2))(√((t−(x/2))^2 )) ∣_0 ^1 =(1−(x/2))(√((1−(x/2))^2 ))+(x/2)(√(x^2 /4)) ∫_0 ^( 3) f(x)dx=∫_0 ^( 2) {(1−(x/2))^2 dx −∫_2 ^( 3) {(1−(x/2))^2 dx+∫_0 ^( 3) (x^2 /4)dx =(2/3)((x/2)−1)^3 ∣_0 ^2 −(2/3)((x/2)−1)^3 ∣_2 ^3 +(x^3 /(12))∣_0 ^3 =(2/3)−(1/(12))+(9/4)=((17)/6)

$${f}\left({x}\right)=\mathrm{2}\int_{\mathrm{0}} ^{\:\mathrm{1}} \sqrt{\left({t}−\frac{{x}}{\mathrm{2}}\right)^{\mathrm{2}} }{dx} \\ $$$$=\left({t}−\frac{{x}}{\mathrm{2}}\right)\sqrt{\left({t}−\frac{{x}}{\mathrm{2}}\right)^{\mathrm{2}} }\:\mid_{\mathrm{0}} ^{\mathrm{1}} \\ $$$$=\left(\mathrm{1}−\frac{{x}}{\mathrm{2}}\right)\sqrt{\left(\mathrm{1}−\frac{{x}}{\mathrm{2}}\right)^{\mathrm{2}} }+\frac{{x}}{\mathrm{2}}\sqrt{\frac{{x}^{\mathrm{2}} }{\mathrm{4}}} \\ $$$$\int_{\mathrm{0}} ^{\:\mathrm{3}} {f}\left({x}\right){dx}=\int_{\mathrm{0}} ^{\:\mathrm{2}} \left\{\left(\mathrm{1}−\frac{{x}}{\mathrm{2}}\right)^{\mathrm{2}} {dx}\right. \\ $$$$\:\:\:\:−\int_{\mathrm{2}} ^{\:\mathrm{3}} \left\{\left(\mathrm{1}−\frac{{x}}{\mathrm{2}}\right)^{\mathrm{2}} {dx}+\int_{\mathrm{0}} ^{\:\mathrm{3}} \frac{{x}^{\mathrm{2}} }{\mathrm{4}}{dx}\right. \\ $$$$\:\:=\frac{\mathrm{2}}{\mathrm{3}}\left(\frac{{x}}{\mathrm{2}}−\mathrm{1}\right)^{\mathrm{3}} \mid_{\mathrm{0}} ^{\mathrm{2}} −\frac{\mathrm{2}}{\mathrm{3}}\left(\frac{{x}}{\mathrm{2}}−\mathrm{1}\right)^{\mathrm{3}} \mid_{\mathrm{2}} ^{\mathrm{3}} \\ $$$$\:\:\:\:\:\:\:+\frac{{x}^{\mathrm{3}} }{\mathrm{12}}\mid_{\mathrm{0}} ^{\mathrm{3}} \\ $$$$\:\:=\frac{\mathrm{2}}{\mathrm{3}}−\frac{\mathrm{1}}{\mathrm{12}}+\frac{\mathrm{9}}{\mathrm{4}}=\frac{\mathrm{17}}{\mathrm{6}} \\ $$

Answered by ajfour last updated on 19/Apr/21

(df/dx)=(x^2 /(x^3 −3x^2 +3x))+((2f)/x) x^2 (((df(x))/dx))−2xf(x)=(x^3 /(x^2 −3x+3)) d(((f(x))/x^2 ))=(1/(x(x^2 −3x+3))) (3/(3x(x^2 −3x+3)))=(1/(3x))+((Ax+B)/(x^2 −3x+3)) ⇒ x^2 −3x+3+3Ax^2 +3Bx=3 ⇒ A=−(1/3), B=1=(3/3) f(x)=x^2 {((ln x)/3)−(1/3)∫(((x−3)dx)/(x^2 −3x+3))+k} f^( 1) (x)=((2xln x)/3)+(x/3)−((x^2 (x−3))/(3(x^2 −3x+3))) +2x(((f(x))/x^2 )−((ln x)/3)) f^( 1) (x)=(x/3)−((x^2 (x−3))/(3(x^2 −3x+3)))+((2f(x))/x) xf^( 1) (x)=(x^2 /3)−((x^2 (x^2 −3x))/(3(x^2 −3x+3)))+2f(x) f^( 1) (x)+xf^( 2) (x)=((2x(x^2 −3x+3)−x^2 (2x−3))/((x^2 −3x+3)^2 ))+2f^( 1) (x) xf^( 2) (x)=−((3x^2 )/((x^2 −3x+3)^2 ))+f^( 1) (x) x(x^2 −3x+3)^2 f^( 2) (x)+3x^2 =(x^2 −3x+3)^2 f^( 1) (x) {(x^2 −3x+3)^2 +2x(2x−3)(x^2 −3x+3)}f^( 2) (x) +x(x^2 −3x+3)^2 f^( 3) (x)+6x =2(x^2 −3x+3)(2x−3)f^( 1) (x) +(x^2 −3x+3)^2 f^( 2) (x) ⇒ 2x(2x−3)(x^2 −3x+3)f^( 2) (x) +x(x^2 −3x+3)^2 f^( 3) (x)+6 =2(x^2 −3x+3)(2x−3)f^( 1) (x) ⇒ 2(2x−3)(3x^2 )=6(x^2 −3x+3) +x(x^2 −3x+3)^2 f^( 3) (x) f^( 3) (x)=((6x^2 (2x−3)−6(x^2 −3x+3))/(x(x^2 −3x+3)^2 )) =((6(2x^3 −4x^2 +3x−3))/(x(x^2 −3x+3)^2 )) let x=t+h f^( 3) (t)=((6(2t^3 +6ht^2 +6h^2 t+h^3 −4t^2 −8ht−4h^2 +3t+3h−3))/((t+h)(t^2 +2ht+h^2 −3t−3h+3)^2 )) let −2h^3 +6h^3 −6h^3 +h^3 −4h^2 +8h^2 −4h^2 −3h+3h−3=0 ⇒ −h^3 −3=0 h=−3^(1/3) ...

$$\frac{{df}}{{dx}}=\frac{{x}^{\mathrm{2}} }{{x}^{\mathrm{3}} −\mathrm{3}{x}^{\mathrm{2}} +\mathrm{3}{x}}+\frac{\mathrm{2}{f}}{{x}} \\ $$$${x}^{\mathrm{2}} \left(\frac{{df}\left({x}\right)}{{dx}}\right)−\mathrm{2}{xf}\left({x}\right)=\frac{{x}^{\mathrm{3}} }{{x}^{\mathrm{2}} −\mathrm{3}{x}+\mathrm{3}} \\ $$$${d}\left(\frac{{f}\left({x}\right)}{{x}^{\mathrm{2}} }\right)=\frac{\mathrm{1}}{{x}\left({x}^{\mathrm{2}} −\mathrm{3}{x}+\mathrm{3}\right)} \\ $$$$\frac{\mathrm{3}}{\mathrm{3}{x}\left({x}^{\mathrm{2}} −\mathrm{3}{x}+\mathrm{3}\right)}=\frac{\mathrm{1}}{\mathrm{3}{x}}+\frac{{Ax}+{B}}{{x}^{\mathrm{2}} −\mathrm{3}{x}+\mathrm{3}} \\ $$$$\:\Rightarrow\:\:{x}^{\mathrm{2}} −\mathrm{3}{x}+\mathrm{3}+\mathrm{3}{Ax}^{\mathrm{2}} +\mathrm{3}{Bx}=\mathrm{3} \\ $$$$\Rightarrow\:\:{A}=−\frac{\mathrm{1}}{\mathrm{3}},\:\:{B}=\mathrm{1}=\frac{\mathrm{3}}{\mathrm{3}} \\ $$$${f}\left({x}\right)={x}^{\mathrm{2}} \left\{\frac{\mathrm{ln}\:{x}}{\mathrm{3}}−\frac{\mathrm{1}}{\mathrm{3}}\int\frac{\left({x}−\mathrm{3}\right){dx}}{{x}^{\mathrm{2}} −\mathrm{3}{x}+\mathrm{3}}+{k}\right\} \\ $$$${f}^{\:\mathrm{1}} \left({x}\right)=\frac{\mathrm{2}{x}\mathrm{ln}\:{x}}{\mathrm{3}}+\frac{{x}}{\mathrm{3}}−\frac{{x}^{\mathrm{2}} \left({x}−\mathrm{3}\right)}{\mathrm{3}\left({x}^{\mathrm{2}} −\mathrm{3}{x}+\mathrm{3}\right)} \\ $$$$\:\:\:\:\:\:+\mathrm{2}{x}\left(\frac{{f}\left({x}\right)}{{x}^{\mathrm{2}} }−\frac{\mathrm{ln}\:{x}}{\mathrm{3}}\right) \\ $$$${f}^{\:\mathrm{1}} \left({x}\right)=\frac{{x}}{\mathrm{3}}−\frac{{x}^{\mathrm{2}} \left({x}−\mathrm{3}\right)}{\mathrm{3}\left({x}^{\mathrm{2}} −\mathrm{3}{x}+\mathrm{3}\right)}+\frac{\mathrm{2}{f}\left({x}\right)}{{x}} \\ $$$${xf}^{\:\mathrm{1}} \left({x}\right)=\frac{{x}^{\mathrm{2}} }{\mathrm{3}}−\frac{{x}^{\mathrm{2}} \left({x}^{\mathrm{2}} −\mathrm{3}{x}\right)}{\mathrm{3}\left({x}^{\mathrm{2}} −\mathrm{3}{x}+\mathrm{3}\right)}+\mathrm{2}{f}\left({x}\right) \\ $$$${f}^{\:\mathrm{1}} \left({x}\right)+{xf}^{\:\mathrm{2}} \left({x}\right)=\frac{\mathrm{2}{x}\left({x}^{\mathrm{2}} −\mathrm{3}{x}+\mathrm{3}\right)−{x}^{\mathrm{2}} \left(\mathrm{2}{x}−\mathrm{3}\right)}{\left({x}^{\mathrm{2}} −\mathrm{3}{x}+\mathrm{3}\right)^{\mathrm{2}} }+\mathrm{2}{f}^{\:\mathrm{1}} \left({x}\right) \\ $$$$\:{xf}^{\:\mathrm{2}} \left({x}\right)=−\frac{\mathrm{3}{x}^{\mathrm{2}} }{\left({x}^{\mathrm{2}} −\mathrm{3}{x}+\mathrm{3}\right)^{\mathrm{2}} }+{f}^{\:\mathrm{1}} \left({x}\right) \\ $$$${x}\left({x}^{\mathrm{2}} −\mathrm{3}{x}+\mathrm{3}\right)^{\mathrm{2}} {f}^{\:\mathrm{2}} \left({x}\right)+\mathrm{3}{x}^{\mathrm{2}} \\ $$$$\:\:\:\:\:=\left({x}^{\mathrm{2}} −\mathrm{3}{x}+\mathrm{3}\right)^{\mathrm{2}} {f}^{\:\mathrm{1}} \left({x}\right) \\ $$$$\left\{\left({x}^{\mathrm{2}} −\mathrm{3}{x}+\mathrm{3}\right)^{\mathrm{2}} +\mathrm{2}{x}\left(\mathrm{2}{x}−\mathrm{3}\right)\left({x}^{\mathrm{2}} −\mathrm{3}{x}+\mathrm{3}\right)\right\}{f}^{\:\mathrm{2}} \left({x}\right) \\ $$$$+{x}\left({x}^{\mathrm{2}} −\mathrm{3}{x}+\mathrm{3}\right)^{\mathrm{2}} {f}^{\:\mathrm{3}} \left({x}\right)+\mathrm{6}{x} \\ $$$$=\mathrm{2}\left({x}^{\mathrm{2}} −\mathrm{3}{x}+\mathrm{3}\right)\left(\mathrm{2}{x}−\mathrm{3}\right){f}^{\:\mathrm{1}} \left({x}\right) \\ $$$$\:\:\:\:\:+\left({x}^{\mathrm{2}} −\mathrm{3}{x}+\mathrm{3}\right)^{\mathrm{2}} {f}^{\:\mathrm{2}} \left({x}\right) \\ $$$$\Rightarrow\:\mathrm{2}{x}\left(\mathrm{2}{x}−\mathrm{3}\right)\left({x}^{\mathrm{2}} −\mathrm{3}{x}+\mathrm{3}\right){f}^{\:\mathrm{2}} \left({x}\right) \\ $$$$\:\:+{x}\left({x}^{\mathrm{2}} −\mathrm{3}{x}+\mathrm{3}\right)^{\mathrm{2}} {f}^{\:\mathrm{3}} \left({x}\right)+\mathrm{6} \\ $$$$\:\:=\mathrm{2}\left({x}^{\mathrm{2}} −\mathrm{3}{x}+\mathrm{3}\right)\left(\mathrm{2}{x}−\mathrm{3}\right){f}^{\:\mathrm{1}} \left({x}\right) \\ $$$$\Rightarrow \\ $$$$\mathrm{2}\left(\mathrm{2}{x}−\mathrm{3}\right)\left(\mathrm{3}{x}^{\mathrm{2}} \right)=\mathrm{6}\left({x}^{\mathrm{2}} −\mathrm{3}{x}+\mathrm{3}\right) \\ $$$$\:\:\:\:\:\:\:\:\:\:+{x}\left({x}^{\mathrm{2}} −\mathrm{3}{x}+\mathrm{3}\right)^{\mathrm{2}} {f}^{\:\mathrm{3}} \left({x}\right) \\ $$$${f}^{\:\mathrm{3}} \left({x}\right)=\frac{\mathrm{6}{x}^{\mathrm{2}} \left(\mathrm{2}{x}−\mathrm{3}\right)−\mathrm{6}\left({x}^{\mathrm{2}} −\mathrm{3}{x}+\mathrm{3}\right)}{{x}\left({x}^{\mathrm{2}} −\mathrm{3}{x}+\mathrm{3}\right)^{\mathrm{2}} } \\ $$$$\:\:\:=\frac{\mathrm{6}\left(\mathrm{2}{x}^{\mathrm{3}} −\mathrm{4}{x}^{\mathrm{2}} +\mathrm{3}{x}−\mathrm{3}\right)}{{x}\left({x}^{\mathrm{2}} −\mathrm{3}{x}+\mathrm{3}\right)^{\mathrm{2}} } \\ $$$${let}\:\:{x}={t}+{h} \\ $$$${f}^{\:\mathrm{3}} \left({t}\right)=\frac{\mathrm{6}\left(\mathrm{2}{t}^{\mathrm{3}} +\mathrm{6}{ht}^{\mathrm{2}} +\mathrm{6}{h}^{\mathrm{2}} {t}+{h}^{\mathrm{3}} −\mathrm{4}{t}^{\mathrm{2}} −\mathrm{8}{ht}−\mathrm{4}{h}^{\mathrm{2}} +\mathrm{3}{t}+\mathrm{3}{h}−\mathrm{3}\right)}{\left({t}+{h}\right)\left({t}^{\mathrm{2}} +\mathrm{2}{ht}+{h}^{\mathrm{2}} −\mathrm{3}{t}−\mathrm{3}{h}+\mathrm{3}\right)^{\mathrm{2}} } \\ $$$${let}\:\:−\mathrm{2}{h}^{\mathrm{3}} +\mathrm{6}{h}^{\mathrm{3}} −\mathrm{6}{h}^{\mathrm{3}} +{h}^{\mathrm{3}} −\mathrm{4}{h}^{\mathrm{2}} +\mathrm{8}{h}^{\mathrm{2}} −\mathrm{4}{h}^{\mathrm{2}} −\mathrm{3}{h}+\mathrm{3}{h}−\mathrm{3}=\mathrm{0} \\ $$$$\Rightarrow\:\:−{h}^{\mathrm{3}} −\mathrm{3}=\mathrm{0} \\ $$$${h}=−\mathrm{3}^{\mathrm{1}/\mathrm{3}} \\ $$$$... \\ $$$$ \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com